Avito Code Challenge 2018 C

C. Useful Decomposition

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Ramesses knows a lot about problems involving trees (undirected connected graphs without cycles)!

He created a new useful tree decomposition, but he does not know how to construct it, so he asked you for help!

The decomposition is the splitting the edges of the tree in some simple paths in such a way that each two paths have at least one common vertex. Each edge of the tree should be in exactly one path.

Help Remesses, find such a decomposition of the tree or derermine that there is no such decomposition.

Input

The first line contains a single integer $\mathrm{nn (2\le n\le 1052\le n\le 105)\; the\; number\; of\; nodes\; in\; the\; tree.}$

Each of the next $\mathrm{n-1n\hspace{0.17em}-\hspace{0.17em}1 lines\; contains\; two\; integers aiai and bibi (1\le ai,bi\le n1\le ai,bi\le n, ai\ne biai\ne bi) —\; the\; edges\; of\; the\; tree.\; It\; is\; guaranteed\; that\; the\; given\; edges\; form\; a\; tree.}$

Output

If there are no decompositions, print the only line containing "No".

Otherwise in the first line print "Yes", and in the second line print the number of paths in the decomposition $\mathrm{mm.}$

Each of the next $\mathrm{mm lines\; should\; contain\; two\; integers uiui, vivi (1\le ui,vi\le n1\le ui,vi\le n, ui\ne viui\ne vi)\; denoting\; that\; one\; of\; the\; paths\; in\; the\; decomposition\; is\; the\; simple\; path\; between\; nodes uiui and vivi.}$

Each pair of paths in the decomposition should have at least one common vertex, and each edge of the tree should be presented in exactly one path. You can print the paths and the ends of each path in arbitrary order.

If there are multiple decompositions, print any.

Examples

input

Copy

4
1 2
2 3
3 4

output

Copy

Yes
1
1 4

input

Copy

6
1 2
2 3
3 4
2 5
3 6

output

Copy

No

input

Copy

5
1 2
1 3
1 4
1 5

output

Copy

Yes
4
1 2
1 3
1 4
1 5

Note

The tree from the first example is shown on the picture below: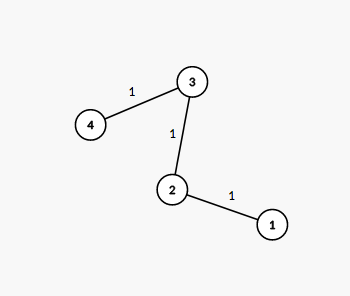The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

The tree from the second example is shown on the picture below: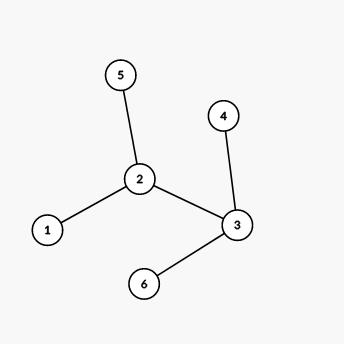We can show that there are no valid decompositions of this tree.

The tree from the third example is shown on the picture below: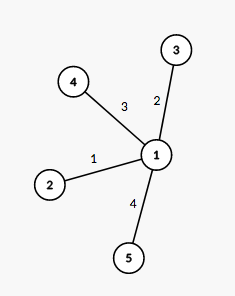The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.

题意  分成任意条路   任意两条路至少有一个交点     而且任意两条路不能有相同的边  输出 路径

解析  可以得到  所有路只有一个交点  所以最多只有一个点的度数大于等于3 才有解决方案 那个点就是交点  以它为起点枚举路径就好了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=998244353,maxn=1e5+50;
#define ios() ios::sync_with_stdio(false),cin.tie(),cout.tie()
vector<int> g[maxn];
int vis[maxn],ans[maxn],cnt;
void dfs(int x)
{
    vis[x]=1;
    int flagg=0;
    for(int i=0;i<g[x].size();i++)
    {
        int u=g[x][i];
        if(vis[u]==0)
        {
            flagg++;
            dfs(u);
        }
    }
    if(flagg==0)
        ans[cnt++]=x;
}
int main()
{
    ios();
    int n;
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int x,y;
        cin>>x>>y;
        g[x].push_back(y);
        g[y].push_back(x);
    }
    int flag=1,sum=0;
    for(int i=1;i<=n;i++)
    {
        if(g[i].size()>=3)
            sum++,flag=i;
    }
    if(sum>=2)
        cout<<"No"<<endl;
    else
    {
        memset(vis,0,sizeof(vis));
        cnt=0;
        dfs(flag);
        cout<<"Yes"<<'
'<<cnt<<endl;
        for(int i=0;i<cnt;i++)
        {
            cout<<flag<<" "<<ans[i]<<endl;
        }
    }
}