from: http://blog.sciencenet.cn/blog-1255140-1025724.html
函数拟合
现实中各种各样的问题都可以归结为函数问题。比如医生诊断疾病,他得到病人检查的各种参数,体温、血压、血检报告和CT扫描的各种数据等,然后判断他是否健康,还是得了什么病。这个例子里,各种参数就是函数的自变量,病人的健康情况是函数值,比如健康是0,有病是1,也可以更具体,肝病是1,胃病是2等。又比如识别物体,输入的是物体的像素数据,输出的是物体的类别,是猫是狗,还是苹果梨子等。
机器学习是从样例中总结出规律,本质上是函数拟合。从有限的样本中得到一个函数,使它能拟合样本数据,然后把它应用到新的样例中。我们学习知识的过程也类似。比如我们每次见了狗,都跟小孩子说这是一条狗,经历过几次后,小孩子就能总结出规律,知道狗是什么样子,以后出现未见过的狗,他也会判断。
神经元模型
人工神经网络的研究受到了真实神经网络的启发。神经元是人工神经网络的基本要素,它表示为:
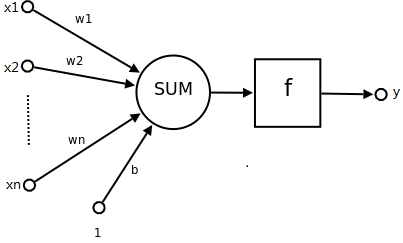
Sum是求和函数,x1、x2……xn是输入,w1、w2、……wn是权重:
Sum(x1,x2,……,xn)= w1x1 + w2x2 +……+ wnxn + b
f是激活函数。最简单的激活函数是符号函数,如下:
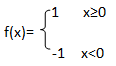
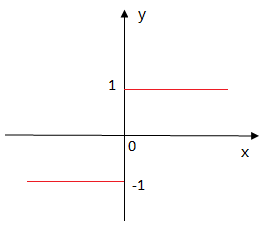
所以这个神经元模型表示的函数是:y=f (x1,x2,……,xn)
=f (w1x1 + w2x2 +……+ wnxn + b)
线性划分
上面的神经元模型虽然简单,但它可以实现很多函数。比如可用它来表示大部分布尔函数。用1和-1分别表示真和假。设置w1=w2=0.5,b=-0.8,这时神经元是逻辑AND函数。将b改为-0.3,则变成OR函数。但它无法表示XOR函数(当x1≠x2时,输出为1,否则为0)。
由于这个神经元函数是线性函数,所以可以把它看作是n维空间的超平面决策器。对于超平面一侧的样例,神经元输出1,另一侧则输出-1。
当空间的点是线性可分时,可用单个神经元划分,否则不行。比如下面的左图,红色的点和蓝色的点可用一根直线分开,这些点可用神经元分类,而右边是XOR函数,无法用直线分开,解决:多层神经刚落。
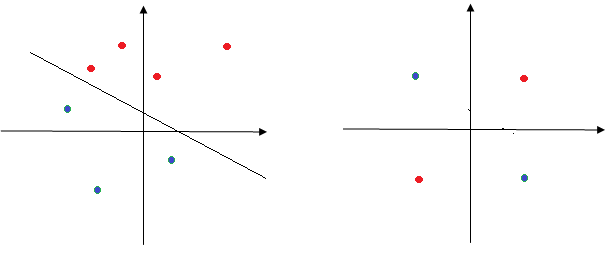
多层网络
单层网络的功能太弱,引入多层网络,除了输入层和输出层外,其他的层是隐藏层。
前馈神经网络是最基本的多层网络,上一层的神经元和下一层的每个神经元都有连接,不能跨层连接,同一层的也不连接。可以看出这实质上是个复合函数。
除了前馈神经网络外,还有其他类型的网络,它们不遵守上面的这些限定。
前馈神经网络

学习算法
教小孩子什么是苹果,先告诉他这几个是苹果,他自己会总结出一些特征。当出现一个梨子时,他若判断为苹果,就告诉他这是错的。他会根据这个梨子和苹果的差异,修改他关于苹果的认知,这样反复几次后,就会掌握苹果这个概念。
学习算法是神经网络中最核心的要素,神经网络的学习和上面小孩子的学习有些相似。学习的目的是获得网络连接的正确权值。有各种各样的学习算法,反向传播算法是很重要的一种。它将网络输出和正确的函数值进行比较,根据两者的差异修改权值,再将修改后得到的网络输出和正确值比较,再根据差异修改,这样多次重复,逐渐缩小两者的差异。
下面是反向传播算法的图示,图中的f(x)是激活函数。
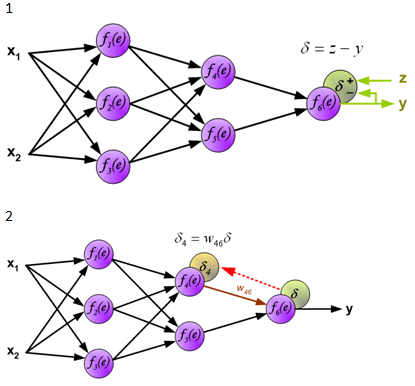
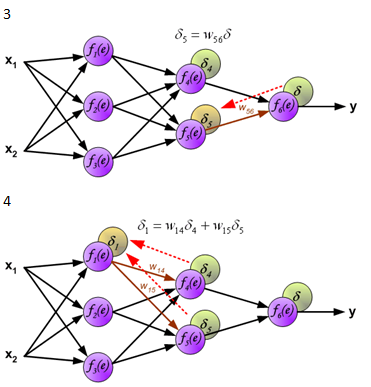



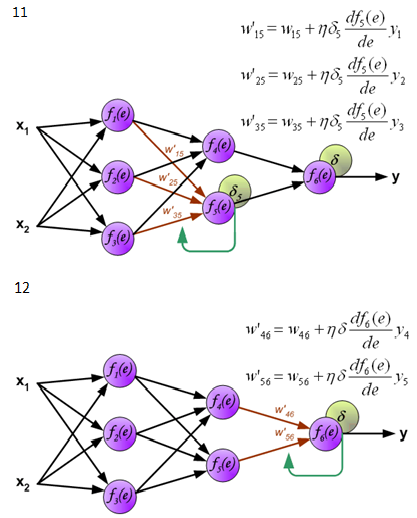
图片来源:http://galaxy.agh.edu.pl/~vlsi/AI/backp_t_en/backprop.html