[Swift]LeetCode979. 在二叉树中分配硬币 | Distribute Coins in Binary Tree

原文地址：https://www.cnblogs.com/strengthen/p/10295198.html 

Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.

In one move, we may choose two adjacent nodes and move one coin from one node to another.  (The move may be from parent to child, or from child to parent.)

Return the number of moves required to make every node have exactly one coin. 

Example 1:

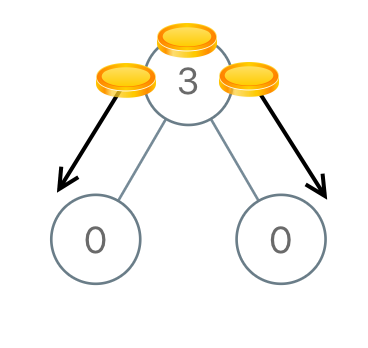
Input: [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

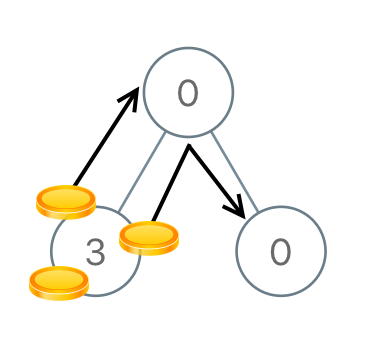
Input: [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves].  Then, we move one coin from the root of the tree to the right child.

Example 3:

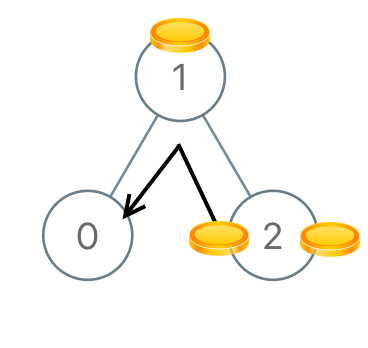
Input: [1,0,2]
Output: 2

Example 4:

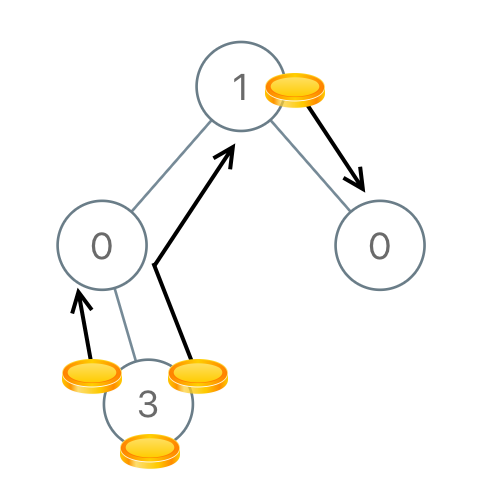
Input: [1,0,0,null,3]
Output: 4 

Note:

1. 1<= N <= 100
2. 0 <= node.val <= N

---

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点。)。

返回使每个结点上只有一枚硬币所需的移动次数。

示例 1：

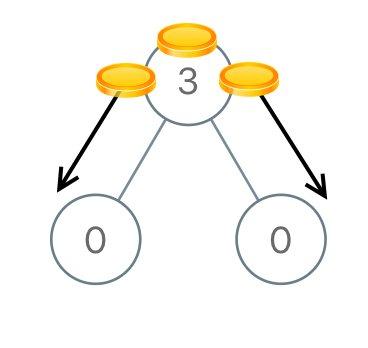
输入：[3,0,0]
输出：2
解释：从树的根结点开始，我们将一枚硬币移到它的左子结点上，一枚硬币移到它的右子结点上。

示例 2：

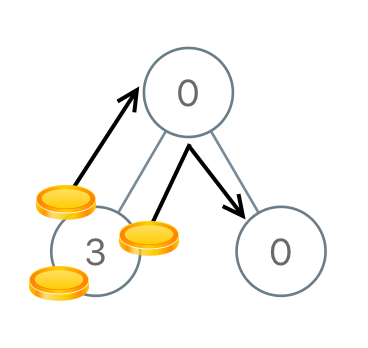
输入：[0,3,0]
输出：3
解释：从根结点的左子结点开始，我们将两枚硬币移到根结点上 [移动两次]。然后，我们把一枚硬币从根结点移到右子结点上。

示例 3：

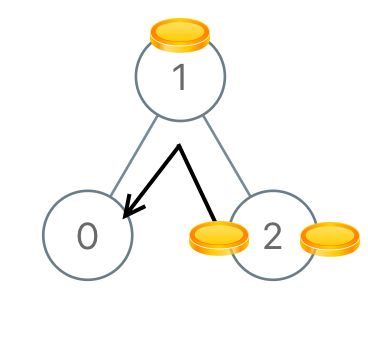
输入：[1,0,2]
输出：2

示例 4：

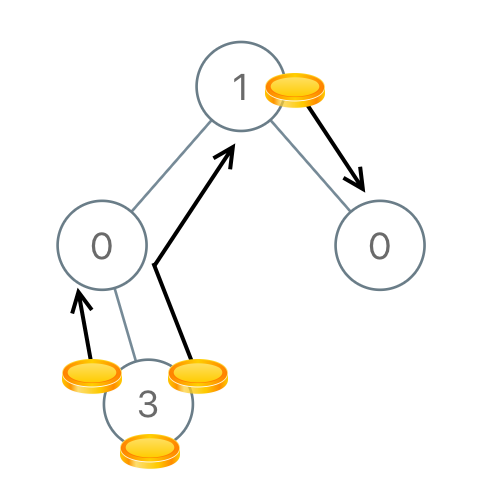
输入：[1,0,0,null,3]
输出：4 

提示：

1. 1<= N <= 100
2. 0 <= node.val <= N

---

28ms 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     public var val: Int
 *     public var left: TreeNode?
 *     public var right: TreeNode?
 *     public init(_ val: Int) {
 *         self.val = val
 *         self.left = nil
 *         self.right = nil
 *     }
 * }
 */
class Solution {
    var ans:Int = 0
    func distributeCoins(_ root: TreeNode?) -> Int {
        if root == nil
        {
            return 0
        }
        travel(root)
        return ans    
    }
    
    func travel(_ node: TreeNode?) -> [Int]
    {
        if node == nil
        {
            return [0, 0]
        }
        var left:[Int] = travel(node!.left)
        var right:[Int] = travel(node!.right)
        if left[0] != left[1]
        {
            ans += abs(left[0] - left[1])
        }
        if right[0] != right[1]
        {
            ans += abs(right[0] - right[1])            
        }
        return [node!.val + left[0] + right[0], 1 + left[1] + right[1]]
    }  
}