java求解两个字符串之间的编辑距离

前言

编辑距离是用来衡量两个字符串之间相似程度的指标，具体表示为字符串A转换为字符串B所需要的最少单字符编辑次数，有插入，删除，替换3种操作，以字符串 horse 和 ros 为例

horse -> rorse，将 h 替换为 r
rorse -> rose，删除 r
rose -> ros，删除 e

编辑距离为3。

使用场景

搜索引擎的拼写纠错就使用到了编辑距离

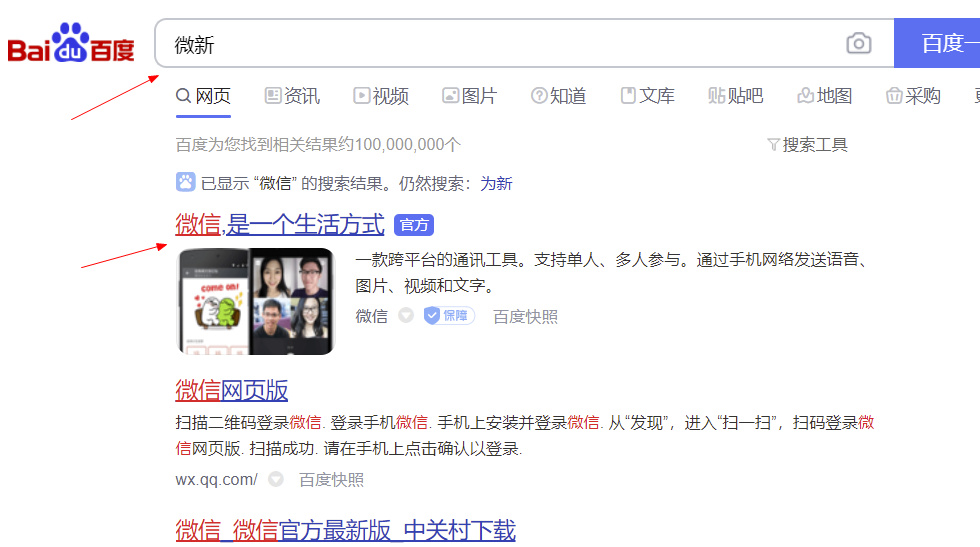
代码实现

class Solution {

  public int minDistance(String word1, String word2) {
    int m = word1.length();
    int n = word2.length();
    int[][] memo = new int[m + 1][n + 1];
    memo[0][0] = 0;
    //要删除的数量
    for (int i = 1; i <= m; i++) {
      memo[i][0] = i;
    }
    //要添加的数量
    for (int i = 1; i <= n; i++) {
      memo[0][i] = i;
    }
    for (int i = 1; i <= m; i++) {
      for (int j = 1; j <= n; j++) {
        if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
          memo[i][j] = memo[i - 1][j - 1];
        } else {
          //取替换，删除，添加中的最小值
          memo[i][j] = Math.min(memo[i - 1][j - 1], Math.min(memo[i - 1][j], memo[i][j - 1])) + 1;
        }
      }
    }
    return memo[m][n];
  }

  public static void main(String[] args) {
    System.out.println(new Solution().minDistance("horse", "ros"));
  }
}

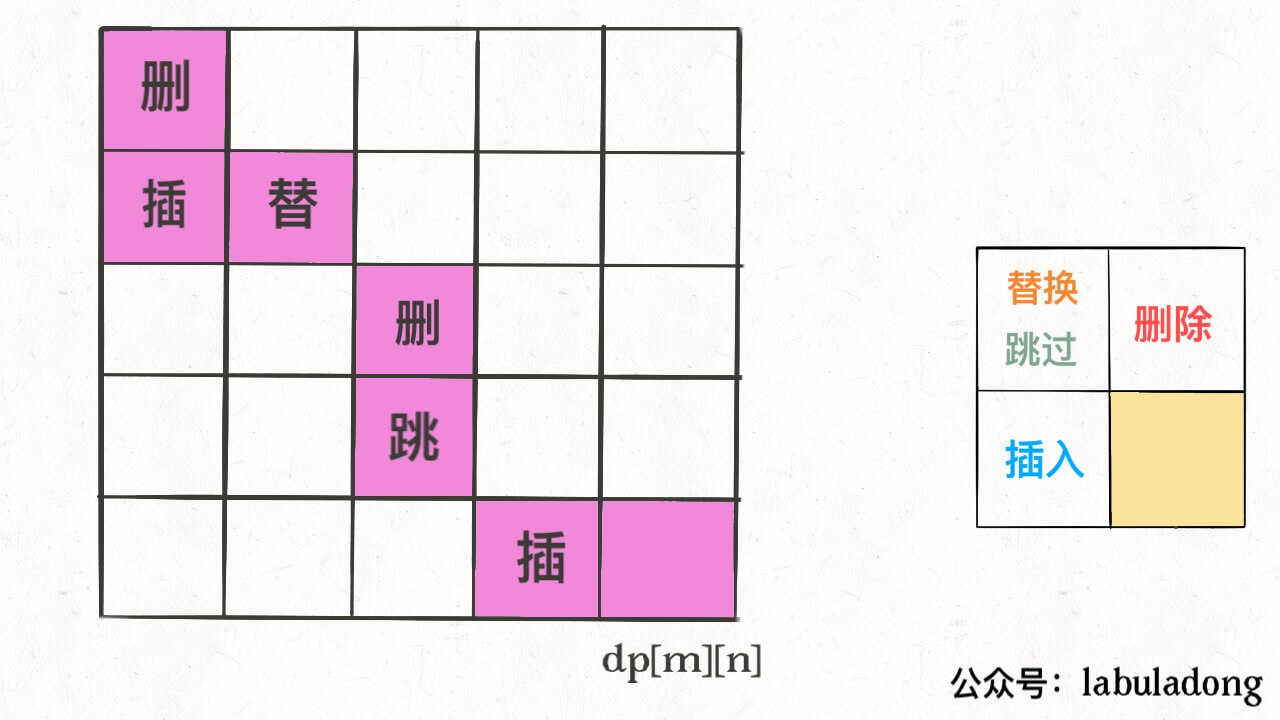
使用动态规划的思想

扩展

通过距离反推出求出编辑距离的操作过程

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

class Solution2 {

  private int[][] minDistance(String word1, String word2) {
    int m = word1.length();
    int n = word2.length();
    int[][] memo = new int[m + 1][n + 1];
    memo[0][0] = 0;
    //要删除的数量
    for (int i = 1; i <= m; i++) {
      memo[i][0] = i;
    }
    //要添加的数量
    for (int i = 1; i <= n; i++) {
      memo[0][i] = i;
    }
    for (int i = 1; i <= m; i++) {
      for (int j = 1; j <= n; j++) {
        if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
          memo[i][j] = memo[i - 1][j - 1];
        } else {
          //取替换，删除，添加中的最小值
          memo[i][j] = Math.min(memo[i - 1][j - 1], Math.min(memo[i - 1][j], memo[i][j - 1])) + 1;
        }
      }
    }
    return memo;
  }

  public List<String> backtrackingPath(String word1, String word2) {
    int[][] memo = minDistance(word1, word2);
    int m = word1.length();
    int n = word2.length();
    List<String> actions = new ArrayList<>();
    while (m >= 0 || n >= 0) {
      if (n > 0 && memo[m][n - 1] + 1 == memo[m][n]) {
        //insert
        actions.add("insert:" + word2.charAt(n - 1));
        n--;
      } else if (m > 0 && memo[m - 1][n] + 1 == memo[m][n]) {
        //delete
        actions.add("delete:" + word1.charAt(m - 1));
        m--;
      } else if (m > 0 && n > 0 && memo[m - 1][n - 1] + 1 == memo[m][n]) {
        //replace
        actions.add("replace:" + word1.charAt(m - 1) + "->" + word2.charAt(n - 1));
        m--;
        n--;
      } else {
        m--;
        n--;
      }
    }
    Collections.reverse(actions);
    return actions;
  }


  public static void main(String[] args) {
    System.out.println(new Solution2().backtrackingPath("horse", "ros"));
    System.out.println(new Solution2().backtrackingPath("intention", "execution"));
    //intention entention extention exention exection execution

  }
}

输出结果为

[replace:h->r, delete:r, delete:e]
[replace:i->e, replace:n->x, delete:t, replace:n->c, insert:u]

参考

详解编辑距离(Edit Distance)及其代码实现
编辑距离详解
经典动态规划：编辑距离
面试准备——动态规划（1）：编辑距离及其回溯路径