使用说明:图形绘制时的插值
interp1 %1-D data interpolation
interpft %使用fft算法插值
%将原数据x转换到频率域,再逆转换回来更密集的数据采样点
spline %一维Cubic spline(三次样条) data interpolation
interp2 %2-D data interpolation
interp3 %3-D data interpolation (table lookup)
注:The interp2 command interpolates between data points. It finds values of a two-dimensional function f(x,y) underlying the data at intermediate points.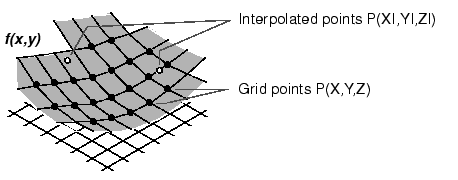

案例1:二维插值显示
[X,Y] =meshgrid(-3:.25:3);Z=peaks(X,Y); %间隔为0.25
[XI,YI]=meshgrid(-3:.33:3,-3:0.05:3); %XI间隔为0.33,YI间隔为0.05
ZI=interp2(X,Y,Z,XI,YI,'cubic');
%设定插值使用的算法。其他选项还有'nearest','linear,'spline'
mesh(X,Y,Z), hold on;axis([-3 3 -3 3 -5 20]);
mesh(XI,YI,ZI+15),hold off; %绘制插值算得的图形
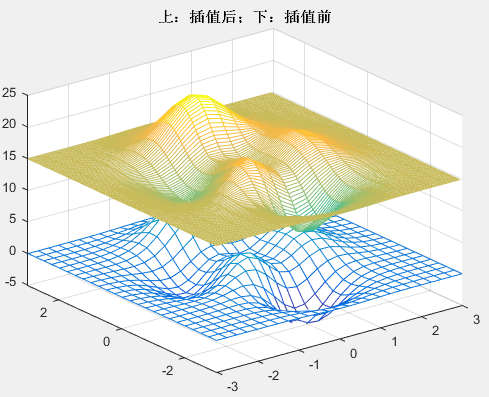
案例2:图像大小的重采样
M = imread('rice.png');
%% 使用插值的方法对图像进行重采样
% the original image
[p,q] = size(M);
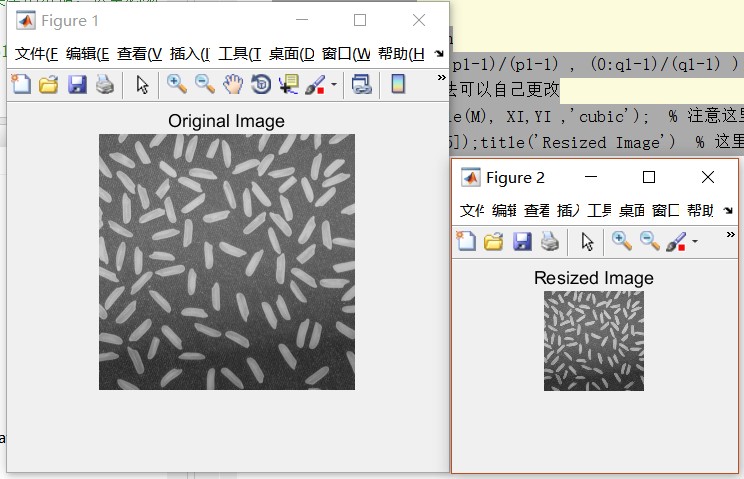
figure;imshow(M);title('Original Image')
% original location
[X,Y] = meshgrid( (0:p-1)/(p-1), (0:q-1)/(q-1) );
% target image size
p1 = 100; q1 = 100;
% new sampling location
[XI,YI] = meshgrid( (0:p1-1)/(p1-1) , (0:q1-1)/(q1-1) );
% the new image 插值方法可以自己更改
M1 = interp2( X,Y,double(M), XI,YI ,'cubic'); % 注意这里的M原本是unit8类型的数据,这里必须转化为double类型的数据
figure;imshow(M1,[0,255]);title('Resized Image') % 这里用imshow显示double类型的图像时要指定显示范围[0,255]
%% 简洁方法(IPT工具箱)
figure;imshow(M);title('Original Image')
% 重采样
p1 = 100; q1 = 100;
M1 = imresize(M,[p1,q1]);
figure;imshow(M1);title('Resized Image')
%案例3:已知点不是规则的的网格点,是无规则的TIN模型,如何插值获得规则网格点上数据
慢慢更新。。。