多智能体博弈强化学习研究综述笔记
1. 摘要要点
- 将博弈理论引入强化学习:
- 可以很好的解决智能体的相互关系
- 可以解释收敛点对应策略的合理性
- 可以用均衡解来替代最优解以求得相对有效的策略。
- 强化学习算法解决不了不存在最优解的问题。
- 论文的内容:
- 近年来出现的强化学习算法
- 当前博弈强化学习算法的重难点及可能突破这些重难点的几个突破方向
2. 多智能体深度强化学习关键科学问题
- 人工智能的发展阶段
- 运算智能:快速计算和记忆存储能力。
- 感知智能:觅觉、听觉、触觉等感知能力。
- 认知智能
- 监督学习:
监督学习解决问题的方法就是靠输入大量的标签数据学到抽象特征幵分类。 - 强化学习:
相比监督学习的标签数据,强化学习只需要带有回报的交互数据。 - 强化学习解决的问题:强化学习主要解决的是序贯决策问题,需要智能体不断的与环境迚行交互和尝试,当智能体通过动作
与环境进行交互时,环境会给智能体一个即时回报,智能体会根据回报评估采取的动作,如果是正向的报则加大采取该动作的
概率,如果是负向的回报则减小采取该动作的概率,同时智能体的动作可能会改变环境,不断重复,最终找到最优策略使得累积
回报的期望最大。(与环境交互,环境返回回报,若回报为正向回报,加大采取该动作的概率,反之减小。不断重复,最终达到
最优策略,使得积累回报的期望最大。)(序贯决策的定义:序贯决策是指按时间顺序排列起来,以得到按顺序的各种决策(策略)
,是用于随机性或不确定性动态系统最优化的决策方法。) - 多智能体VS单智能体:
- 多智能体深度强化学习要考虑的动作和状态空间都更大
- 每个智能体的回报不仅和环境有关,与其他智能体的动作也紧密联系
- 由单智能体系统向多智能体系统过渡时主要存在的难点
- 维度爆炸。(由于动作空间、状态空间和参数数量大幅度增加)
解决方式:
- 采用混合型训练机制,即集中式训练分布式执行(CTDE)
- 基于伪计数的探索算法,算法通过设计满足一定性质的密度模型来评估频次,计算在连续空间下具有泛化性的伪计数提高
探索效率,缓解维数爆炸问题。
- 环境非平稳性。(由于环境状态转移函数取决于联合动作)
解决方式:
- 采用 AC框架,通过在训练过程中获得其它智能体的信息和行动,智能体不会经历环境动态的意外变化
- 采用对手建模,通过模拟其他智能体的策略,可以稳定智能体的训练过程
- 利用元学习更快适应非平稳性环境
- 信度分配。
解决方式:
- 平均分配、差分回报分配、优势函数分配以及 Deepmind提出的基于情景记忆检索 TVT 算法
- 维度爆炸。(由于动作空间、状态空间和参数数量大幅度增加)
- 博弈类型
- 标准型博弈:如囚徒困境。
- 扩展式博弈:如围棋
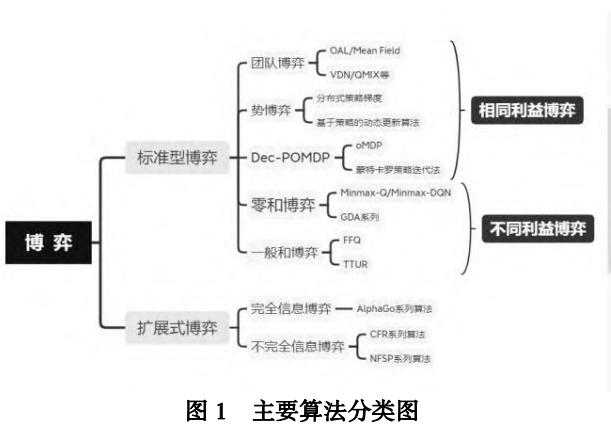
- 博弈论的中心思想:是为博弈建立一个策略交互模型,博弈论中均衡解是让博弈玩家都满意的策略组合,通过展示玩家最终会
采用哪些策略来描述博弈的结果。(均衡解:让玩家都满意,博弈结果:玩家最终会选择的策略)
2. 多智能体博弈强化学习基本概念 - 马尔可夫决策过程
- 马尔可夫性质:当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句
话说,在给定现在状态时,它与过去状态(即该过程的历史路径)是条件独立的,那么此随机过程即具有马尔可夫性质。 - MDP包含一组交互对象,即智能体和环境。
- 智能体(agent):MDP中进行机器学习的代理,可以感知外界环境的状态进行决策、对环境做出动作并通过环境的反馈调整决策。
- 环境(environment):MDP模型中智能体外部所有事物的集合,其状态会受智能体动作的影响而改变,且上述改变可以完全或部
分地被智能体感知。环境在每次决策后可能会反馈给智能体相应的奖励。
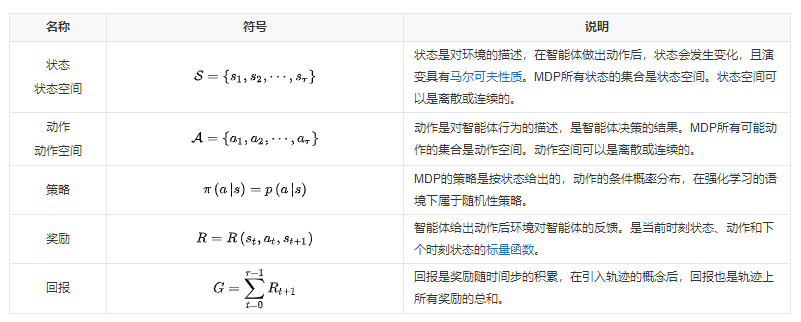
- MDP的求解目标:找到期望回报值最大的最优策略,一般用最优状态动作值函数形式化表彾期望回报:
 。
。 - 多智能体马尔可夫决策过程:当智能体的数量超过一个,同时环境的改变和每个智能体的回报取决于所有智能体的动作和当前状态。
- 马尔可夫性质:当一个随机过程在给定现在状态及所有过去状态情况下,其未来状态的条件概率分布仅依赖于当前状态;换句
- 随机博弈:随机博弈可以看成 MDP 向多人博弈的推广。
- 定义:由如下的六元组定义:
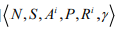 ,其中 N 为
,其中 N 为
博弈玩家的个数,当玩家的个数为 1 时,即退化为 MDP,Ai为第 i 个玩家的动作,A-i为除第 i 个玩家外其他玩家的动作,记为: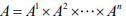 ,
,
Ri为第 i 个玩家的回报函数,当每个玩家的回报函数相同时则称此博弈为团队博弈(Team Games)。 (当N=1时,随机博弈变为马尔可夫博弈。当R1=R2=....时,博弈为团队博弈)
- 定义:由如下的六元组定义:
- 部分可观察的随机博弈
- 定义:部分可观察的随机博弈(POSG)是在随机博弈的基础上对玩家所能观察到的信息迚行了一定的约束,具体表示为
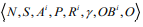 ,其中
,其中
OBi为第i个玩家的观测集,联合观测集为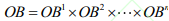 ,O为S×A—>[0,1]的观测函数。
,O为S×A—>[0,1]的观测函数。
去中心化的部分可观察马尔可夫决策过程(Dec-POMDP)是特殊情况下的 POMDP,即所有智能体的回报函数都相同: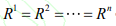
- 定义:部分可观察的随机博弈(POSG)是在随机博弈的基础上对玩家所能观察到的信息迚行了一定的约束,具体表示为
- 纳什均衡
- 定义:纳什均衡就是一组策略
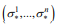 ,该策略使得每个玩家在其他玩家策略不变的情冴下,
,该策略使得每个玩家在其他玩家策略不变的情冴下,
该玩家的收益不会减少,即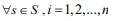 ,都有如下不等式:
,都有如下不等式: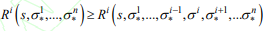
- 定义:纳什均衡就是一组策略
- 元博弈