Greenhouse-Geisser；统计结果报告；效应力大小介绍

转自博客 http://blog.sina.com.cn/s/blog_4d25466d0101p47z.html

 

===============================================================================
Greenhouse-Geisser  一般在ANOVA的统计分析常用，在结果报告中我很困惑其df的报告。今天特意把这个问题弄个明白：
自由度是否报告校正后的，让我很困恼，有网友说：即便校正也不需要报告校正后自由度，只报告原来非校正的。或者看看文献里如何报告的。有位发表过脑电文章的在国内科研单位工作的网友说：是必须报告校正后的，也一般报告四舍五入的整数值即可。
如下是源自：https://statistics.laerd.com/statistical-guides/sphericity-statistical-guide-2.php

This is to counteract the fact that when the assumption of sphericity is violated, there is an increase in Type I errors due to the critical values in the F-table being too small. These corrections attempt to correct this bias.---校正的目的
epsilon (referred to as ）具体是指：如下的红线框旁边的（p大于0.05，所以这个是没有违反球形检验）：

An epsilon of 1 (i.e., ε = 1) indicates that the condition of sphericity is exactly met. The further epsilon decreases below 1 (i.e., ε < 1), the greater the violation of sphericity. Therefore, you can think of epsilon as a statistic that describes the degree to which sphericity has been violated.

当ε = 1时，说明这个值就是满足球形检验；但是当这个值越是小于1时，则越不满足违反了球形检验。

Greenhouse-Geisser Correction

Greenhouse-Geisser Correction为了校正F-分布的自由度进行估计epsilon;比如在违反了球形检验，就可以使用该检验。自由度也要相应的变化：

The Greenhouse-Geisser procedure estimates epsilon (referred to as ) in order to correct the degrees of freedom of the F-distribution as has been mentioned previously, and shown below:

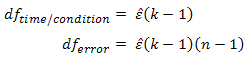
Using our prior example, and if sphericity had been violated, we would have:

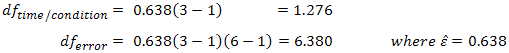
So our F-test result is corrected from F (2,10) = 12.534, p = .002 to F (1.277,6.384) = 12.534, p= .009 (degrees of freedom are slightly different due to rounding). The correction has elicited a more accurate significance value. It has increased the p-value to compensate for the fact that the test is too liberal when sphericity is violated.注意这里的df有相应的变化。

Huynd-Feldt Correction

违反了球形检验，除了用上述的Greenhouse-Geisser,还可以使用Huynd-Feldt Correction

As with the Greenhouse-Geisser correction, the Huynd-Feldt correction estimates epsilon (represented as ) in order to correct the degrees of freedom of the F-distribution as shown below:

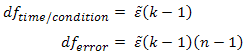
Using our prior example, and if sphericity had been violated, we would have:

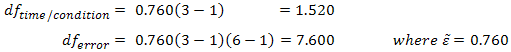
So our F test result is corrected from F (2,10) = 12.534, p = .002 to F (1.520,7.602) = 12.534, p= .005 (degrees of freedom are slightly different due to rounding). As with the Greenhouse-Geisser correction, this correction has elicited a more accurate significance value; it has increased the p-value to compensate for the fact that the test is too liberal when sphericity is violated.

The Greenhouse-Geisser correction tends to underestimate epsilon (ε) when epsilon (ε) is close to 1 (i.e., it is a conservative correction), whilst the Huynd-Feldt correction tends to overestimate epsilon (ε) (i.e., it is a more liberal correction). Generally, the recommendation is to use the Greenhouse-Geisser correction, especially if estimated epsilon (ε) is less than 0.75. However, some statisticians recommend using the Huynd-Feldt correction if estimated epsilon (ε) is greater than 0.75. In practice, both corrections produce very similar corrections, so if estimated epsilon (ε) is greater than 0.75, you can equally justify using either.（相对来说：Greenhouse-Geisser更保守，Huynd-Feldt correction更自由。一般建议用Greenhouse-Geisser。但是，当estimated epsilon (ε)大于0.75时，就需使用Huynd-Feldt correction。在具体操作中，两种校正是相似的，因此当estimated epsilon (ε)大于0.75时，两种都可以用。）

另外，一篇文献里这么提及：
http://www.uccs.edu/Documents/humanneurophysiologylab/07 kisley et al 2005 with erratum.pdf
All significance tests were two-tailed at the 0.05 level. To protect against Type I errors, the degrees of freedom for all repeated measures ANOVAs were adjusted by the method of Greenhouse and Geisser[53]. All waveform amplitudes,whether from positive- or negative-going waves, arereported here as absolute value.


All statistically significant effects were corrected using the Greenhouse–Geisser method (Greenhouse and Geisser, 1959 ){S.W. Greenhouse, S. Geisser--On methods in the analysis of profile data  Psychometrika, 24 (1959), pp. 95–112}----一般ERP脑电分析部分，无论球形检验是否显著，都会考虑用greenhouse-geisser校正。

========================================================================

如何报告结果，转自网易博客的一篇文章：

http://bcaoyuan.blog.163.com/blog/static/210343052201342913053893/  转篇文章：

http://facelab.org/debruine/Teaching/Meth_A/files/Reporting_Statistics.pdf

一、一般原则：

不同的学科与杂志可能要求不一样，但一般来说，可以参考一下格式报告：

1、小数点的保留：

a、大于100：报告整数（如：1034.963报告1035）

b、10-100：1位小数点（如：11.4378报告11.4）

c、0.10-10：2位小数点

d、0.001-0.10：3位小数点

e、小于0.001：报告到第一位非0的位数（注意4舍五入）

注意：

a、整数如人数不要加小数点。N=5不要写成N=5.0；

b、p=.000时报告p<.001，其余均报告精确p值；一般默认双尾，单尾需特殊说明；

c、省略0：如p值，r值以及偏eta-squared (ηp2)。

2、统计量缩写（斜体字体，不写缩写不用斜体，在等号“=”前后需有空格）：

a、均数、标准差：（M = 3.45, SD = 1.21）；

b、Mann-Whitney U检验：（U = 67.5, p = .034, r = .38）；

c、Wilcoxon signed-ranks检验：（Z = 4.21, p < .001）；

d、标准Z检验：（Z = 3.47, p = .001）；

e、t检验：（t(19) = 2.45, p = .031, d = 0.54）；

f、ANOVA：（F(2, 1279) = 6.15, p = .002, ηp2 = 0.010）；

g、Pearson相关：（r(1282) = .13, p < .001）。

注：推断统计一般以以下方式报告：

“统计量(自由度) = , p = , effect size （统计量） = ”

 

二、结果报告：

1、描述统计：基本资料如：年龄等，报告用表或者文字，但不要两者兼用。

范例：The average age of participants was 25.5 years (SD = 7.94).

The age of participants ranged from 18 to 70 years (M = 25.5, SD = 7.94). Age was non-normally distributed, with skewness of 1.87 (SE = 0.05) and kurtosis of 3.93 (SE = 0.10)

Participants were 98 men and 132 women aged 17 to 25 years (men: M = 19.2,SD = 2.32; women: M = 19.6, SD = 2.54).

2、非参检验：不要报告均数和标准差；在表里或文字报告中位数与全距；斜体U或Z，测量的effect size即r，(r = Z / √N)。

U检验（独立样本）范例：A Mann-Whitney test indicated that self-rated attractiveness was greater for women who were not using oral contraceptives (Mdn = 5) than for women who were using oral contraceptives (Mdn = 4), U = 67.5, p = .034, r = .38.

Z检验（相关样本）范例：A Wilcoxon Signed-ranks test indicated that femininity was preferred more in female faces (Mdn = 0.85) than in male faces (Mdn = 0.65), Z = 4.21, p < .001, r = .76.

频数Z检验（相关样本）范例：A sign test indicated that femininity was preferred more in female faces than in male faces, Z = 3.47, p = .001.

3、t检验：报告统计量t，自由度，p与effect size即Cohen’s d。

单样本范例：One-sample t-test indicated that femininity preferences were greater than the chance level of 3.5 for female faces (M = 4.50, SD = 0.70), t(30) = 8.01, p < .001, d = 1.44, but not for male faces (M = 3.46, SD = 0.73), t(30) = -0.32, p = .75, d = 0.057.

The number of masculine faces chosen out of 20 possible was compared to the chance value of 10 using a one-sample t-test. Masculine faces were chosen more often than chance, t(76) = 4.35, p = .004, d = 0.35.

4、相关样本t检验：与独立样本t检验一样。

A paired-samples t-test indicated that scores were significantly higher for the pathogen subscale (M = 26.4, SD = 7.41) than for the sexual subscale (M = 18.0, SD = 9.49), t(721) = 23.3, p < .001, d = 0.87.

Scores on the pathogen subscale (M = 26.4, SD = 7.41) were higher than scores on the sexual subscale (M = 18.0, SD = 9.49), t(721) = 23.3, p < .001, d = 0.87. A onetailed p-value is reported due to the strong prediction of this effect.

5、方差分析：需报告两个自由度，先组间，后组内，中间用逗号和空格隔开，如：F(1, 237) = 3.45。

a、one-way ANOVAs与事后检验（post-hocs）：Analysis of variance showed a main effect of self-rated attractiveness (SRA) on preferences for femininity in female faces, F(2, 1279) = 6.15, p = .002, ηp2 = .010. Posthoc analyses using Tukey’s HSD indicated that femininity preferences were lower for participants with low SRA than for participants with average SRA (p = .014) and high SRA (p = .004), but femininity preferences did not differ significantly between participants with average and high SRA (p = .82).

b、2-way Factorial ANOVAs ：A 3x2 ANOVA with self-rated attractiveness (low, average, high) and oral contraceptive use (true, false) as between-subjects factors revealed a main effects of SRA, F(2, 1276) = 6.11, p = .002, ηp2 = .009, and oral contraceptive use, F(1, 1276) = 4.38, p = .037, ηp2 = 0.003. These main effects were not qualified by an interaction between

SRA and oral contraceptive use, F(2, 1276) = 0.43, p = .65, ηp2 = .001.

c、3-way ANOVAs与更多因素的方差分析：虽然一些书会让我们报告所有的主效应与交互作用，即使结果不显著，这样可以简化对于复杂实验设计（如3因素或更多因 素）结果的理解。报告所有的显著效应和预测效应，即使结果不显著。如果有多于两个和你的主要假设无关的因素不显著（如，你预测它们三者之间存在交互作用， 但没有任何主效应或两因素的交互作用），你可以概括如下：A mixed-design ANOVA with sex of face (male, female) as a within-subjects factor and self-rated attractiveness (low, average, high) and oral contraceptive use (true, false) as between-subjects factors revealed a main effect of sex of face, F(1, 1276) = 1372, p < .001, ηp2 = .52. This was qualified by interactions between sex of face and SRA, F(2, 1276) = 6.90, p = .001, ηp2 = .011, and between sex of face and oral contraceptive use, F(1, 1276) = 5.02, p = .025, ηp2 = .004. The predicted interaction among sex of face, SRA and oral contraceptive use was not significant, F(2, 1276) = 0.06, p = .94, ηp2 < .001. All other main effects and interactions were non-significant and irrelevant to our hypotheses, all F ≤ 0.94, p ≥ .39, ηp2 ≤ .001.

注1：即和我们假设相关的，不管结果显不显著，均需详细报告，其他结果可以概括报告。

注2：球形检验与矫正（Violations of Sphericity and Greenhouse-Geisser Corrections）：方差分析对违背球形检验是不能容忍的，但很容易矫正，若被试内水平多于2个时，检查Mauchly’s test是否显著，如果显著，报告chi-squared (χ2)，自由度，p与epsilon (ε)；然后报告所有涉及此因素的Greenhouse-Geisser的校正值（保留适当的小数位数）。当被试内只有两个水平时，chi-squared (χ2)为.000且没有p值，不需要矫正。如：Data were analysed using a mixed-design ANOVA with a within-subjects factor of subscale (pathogen, sexual, moral) and a between-subject factor of sex (male, female). Mauchly’s test indicated that the assumption of sphericity had been violated (χ2(2) = 16.8, p < .001), therefore degrees of freedom were corrected using Greenhouse-Geisser estimates of sphericity (ε = 0.98). Main effects of subscale, F(1.91, 1350.8) = 378, p < .001, ηp2 = .35, and sex, F(1, 709) = 78.8, p < .001, ηp2 = . 10, were qualified by an interaction between subscale and sex, F(1.91, 1351) = 30.4, p < .001, ηp2 = .041.

d、ANCOVA 协方差分析：An ANCOVA [between-subjects factor: sex (male, female); covariate: age] revealed no main effects of sex, F(1, 732) = 2.00, p = .16, ηp2 = .003, or age, F(1, 732) = 3.25, p = .072, ηp2 = .004, and no interaction between sex and age, F(1, 732) = 0.016, p = .90, ηp2 < .001.

The predicted main effect of sex was not significant, F(1, 732) = 2.00, p = .16, ηp2 = .003, nor was the predicted main effect of age, F(1, 732) = 3.25, p = .072, ηp2 = .004. The interaction between sex and age were also not significant, F(1, 732) = 0.016, p = .90, ηp2 < .001.

6、相关：Preferences for femininity in male and female faces were positively correlated, Pearson’s r(1282) = .13, p < .001.

 

参考文献：

American Psychological Association. (2005). Concise Rules of APA Style. Washington, DC: APA Publications.

Field, A. P., & Hole, G. J. (2003). How to design and report experiments. London: Sage Publications.

===============================================================================================
http://mcgraw-hill.co.uk/openup/harris/b5.html

Size according to Cohen (1988)	Eta squared (% variance explained by your IV)	Cohen's d (in standard deviations)
Small	.01 (1%)	.2
Medium	.06 (6%)	.5
Large	.14 (14%)	.8

===============================================================================================

回归模型中，effect size f 2 的计算：

 

即等于拿第二层的R平方减去第一层的R平方，再除以1减第二层的R平方。

如果有三层的话，则是：拿第三层的R平方减去第二层的R平方，再除以1减第三层的R平方。

 

Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, New Jersey: Lawrence Erlbaum Associates.

如上的效应力则为：f的平方=（0.22-0.062）/(1-0.22)

三层的线性回归，第三层的效应力则为：f的平方=（0.267-0.22）/(1-0.267)