[Java] ConcurrentMap 分析和思考

预备知识：Java HashMap and HashSet 的实现机制

由预备知识可以知道hashmap 的存储结构为：

   

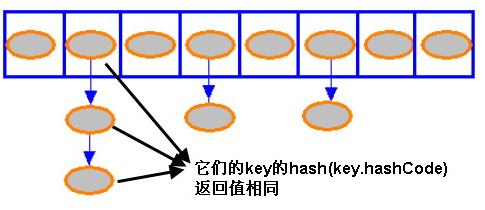
（图像来自http://www.ibm.com/developerworks/cn/java/j-lo-hash/）

也是说：一个hashmap 内部含有一个Entity 类行的数组，这个数组中的元素都是Entity。实际上我们放入map 中的key 和 value 就对应一个Entity 对象，这个Entity 对象包含一个key、value、hashcode（key 的）和一个Entity 的引用，通过这个引用，Entity 可以形成一个链表。在图中，蓝色矩形方框代表数组，橙色椭圆代表Entity 对象。

注意HashMap 类不是线程安全的。

ConcurrentMap  主要的子类是ConcurrentHashMap。

原理：一个ConcurrentHashMap 由多个segment 组成，每个segment 包含一个Entity 的数组。这里比HashMap 多了一个segment 类。该类继承了ReentrantLock 类，所以本身是一个锁。当多线程对ConcurrentHashMap 操作时，不是完全锁住map， 而是锁住相应的segment 。这样提高了并发效率。

构造函数的分析：

/**
     * Creates a new, empty map with a default initial capacity (16),
     * load factor (0.75) and concurrencyLevel (16).
     */
    public ConcurrentHashMap() {
        this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR, DEFAULT_CONCURRENCY_LEVEL);
    }

这是ConcurrentHashMap 的无参构造函数，可以看到默认大小为16，负载因子0.75，并发级别为16.

Put 函数的分析：

/**
     * Maps the specified key to the specified value in this table.
     * Neither the key nor the value can be null.
     *
     * <p> The value can be retrieved by calling the <tt>get</tt> method
     * with a key that is equal to the original key.
     *
     * @param key key with which the specified value is to be associated
     * @param value value to be associated with the specified key
     * @return the previous value associated with <tt>key</tt>, or
     *         <tt>null</tt> if there was no mapping for <tt>key</tt>
     * @throws NullPointerException if the specified key or value is null
     */
    public V put(K key, V value) {
        if (value == null)
            throw new NullPointerException();
        int hash = hash(key.hashCode());
        return segmentFor(hash).put(key, hash, value, false);
    }

可以看出通过hash() 函数得到key 的哈希值，在得到相应的segment，在通过segment 存储Entity。

同时为了避免“检测再修改”（有条件线程安全参见[2]）等并发问题，ConcurrentHashMap 提供了putIfAbsent(K key, V value)  方法，当key 不存在时，添加。（key 的存在靠两个条件，一个是key的hashcode方法，另外一个是key 的equal 方法）

优点：由于对对应segment  加锁，而不是锁定整个map，并发性得到了提高。能够直接提高插入、检索以及移除操作的可伸缩性。

缺点：当遍历map 中的元素时，需要获取所有的segment 的锁，使用遍历时慢。锁的增多，占用了系统的资源。使得对整个集合进行操作的一些方法（例如 size() 或 isEmpty() ）的实现更加困难，因为这些方法要求一次获得许多的锁，并且还存在返回不正确的结果的风险。

参考资料：

1 通过分析 JDK 源代码研究 Hash 存储机制

2 Java 理论与实践: 并发集合类

3 Java 理论与实践: 构建一个更好的 HashMap