图
图的概念
https://www.cnblogs.com/iwehdio/p/12356299.html
-
图 G = ( V ;E )。
V 是顶点集,E 是连边集。用 n 来表示顶点的数量,用 e 来表示连边的数量。在图中,两个顶点之间具对应关系则称为邻接,用两个顶点间的连边表示。而两个顶点与这条连边具的关系成为关联。
-
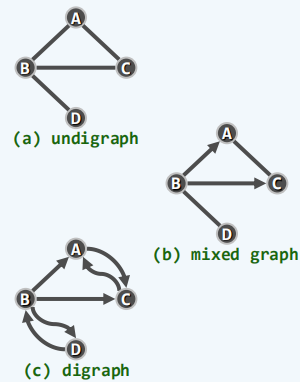
有无向
如果邻接顶点 u 和 v 的次序无所谓则( u,v )为无向边。如果邻接顶点 u 和 v 的方向被规定了,则( u,v )为有向边。所边均无方向的图,称为无向图。所边均方向的图,称为向图。向边与无向边混合的成为混合图。向图可以表示无向图和混合图。
-
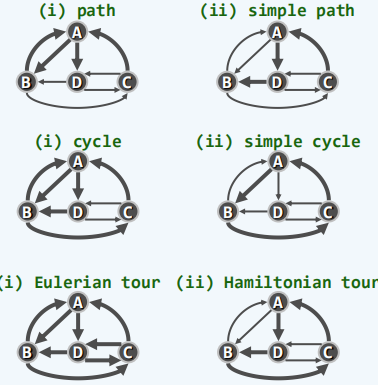
有无环
路径是,一系列的顶点按照邻接关系构成的序列。如果一条路径中不含重复的节点,则称为简单路径。如果路径的起始节点都是一个节点,则称为环路。如果一个有向图中不包含任何环路,则称为有向无环图。欧拉环路:经过所的向边恰好一次的环路。哈密尔顿环路:经过所有的顶点恰好一次的环路
-
最小支撑树
为每一边e指定一个权重,比如wt(e)
即为边e的权重。各边均带权重的图,称作带权图,时也简称网络(network,记作G(V, E, wt())。
同一网络的支撑树中权重最小的为最小支撑树

图的实现
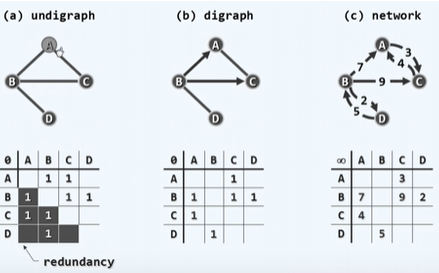
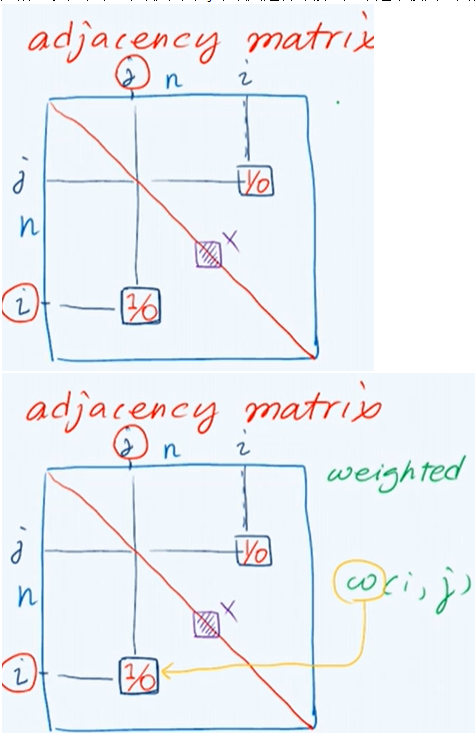
邻接矩阵
邻接矩阵:描述两个顶点之间的邻接关系。如果图中 n 个顶点,对于有向图是 n 行 n 列的方阵,第 i 行第 j 列的元素,表征了第 i 个顶点与第 j 个顶点是否邻接。如果是带权图,只需将元素的值改为权值。
package com.atguigu.prefect;
import java.util.LinkedList;
import java.util.List;
/**
* @anthor shkstart
* @create 2020-08-06 19:48
*/
public class AdjMatrixGraph<T> {
protected List<T> vertexlist;
//顺序表存储的顶底集合
protected int[][] adjmatrix;
//图的邻接矩阵,用二维数组表示
private final int MAX_WEIGHT = 99999;
//设置最大权值,设置成常量
public AdjMatrixGraph(int size){
size = size<10?10:size;
this.vertexlist = new LinkedList<>();
//构造容量为size的空顺序表
this.adjmatrix = new int[size][size];
for (int i=0;i<size;i++){
//初始化邻接矩阵
for (int j=0;j<size;j++){
this.adjmatrix[i][j] = (i==j)?0:MAX_WEIGHT;
}
}
}
public AdjMatrixGraph(T[] vertices,Edge[] edges){
this(vertices.length);
if(vertices == null)
return;
for (int i=0;i<vertices.length;i++)
insertVertex(vertices[i]);
if(edges!=null)
for (int j=0;j<edges.length;j++)
insertEdge(edges[j]);
}
public int vertexCount(){
return this.vertexlist.size();
}
//返回定点顺序表的元素个数
public T get(int i){
return this.vertexlist.get(i);
}
//返回第i个定点的元素
public int getWeight(int i,int j){
return this.adjmatrix[i][j];
}
//返<vi,vj>边的权值
public String toString(){
String str = "顶点集合:"+this.vertexlist.toString()+"n邻接矩阵:n";
int n = this.vertexCount();
for(int i=0;i<n;i++){
for(int j=0;j<n;j++)
str += this.adjmatrix[i][j] == MAX_WEIGHT?" $":" "+this.adjmatrix[i][j];
str +="n";
}
return str;
}
public int insertVertex(T x){
this.vertexlist.add(x); //顺序表追加元素,自动扩充
if(this.vertexCount()>this.adjmatrix.length){ //若二维数组不足,则扩充
int temp[][] = adjmatrix,i,j; //定义了局部变量i,j;
this.adjmatrix = new int[temp.length*2][temp.length*2]; //二维数组扩充2倍
for(i=0;i<temp.length;i++){
for(j=0;j<temp.length;j++)
this.adjmatrix[i][j] = temp[i][j];
for(j=temp.length;j<temp.length*2;j++)
this.adjmatrix[i][j] = MAX_WEIGHT;
}
for(i=temp.length;i<temp.length*2;i++)
for(j=0;j<temp.length*2;j++)
this.adjmatrix[i][j] = (i == j)?0:MAX_WEIGHT;
}
return this.vertexlist.size()-1; //返回插入顶点的序号
}
public void insertEdge(int i,int j,int weight){ //插入一条边
int n = this.vertexCount();
if(i>=0&&i<n&&j>=0&&j<n&&this.adjmatrix[i][j]==MAX_WEIGHT&&i!=j)
this.adjmatrix[i][j] = weight;
}
public void insertEdge(Edge edge){
this.insertEdge(edge.start, edge.dest, edge.weight);
}
public void removeEdge(int i,int j){ //删除一条边
if(i>=0&&i<vertexCount()&&j>=0&&j<vertexCount()&&i!=j)
this.adjmatrix[i][j] = MAX_WEIGHT;
}
public void removeVertex(int i){ //删除顶点以及和顶点有关系的边
int n = this.vertexCount();
if(i<0||i>n)
return;
this.vertexlist.remove(i);
for(int j=0;j<i;j++)
for(int k=i+1;k<n;k++)
this.adjmatrix[j][k-1] = this.adjmatrix[j][k]; //元素向左移一行
for(int j=i+1;j<n;j++)
for(int k=0;k<i;k++)
this.adjmatrix[j-1][k] = this.adjmatrix[j][k]; //元素向上移一行
for(int j=i+1;j<n;j++)
for(int k=i+1;k<n;k++)
this.adjmatrix[j-1][k-1] = this.adjmatrix[j][k];
}
static class Edge implements Comparable<Edge> {
public int start,dest,weight;
public Edge(int start,int dest,int weight){
this.start = start;
this.dest = dest;
this.weight = weight;
}
public String toString(){
return "("+start+","+dest+","+weight+")";
}
public int compareTo(Edge e) {
// TODO Auto-generated method stub
if(this.start!=e.start)
return this.start - e.start;
return this.dest - e.dest;
}
}
public static void main(String[] args){
String[] verices = {"A","B","C","D","E"};
Edge edges[] = {new Edge(0,1,5),new Edge(0,3,2),new Edge(1,0,5),
new Edge(1,2,7),new Edge(1,3,6),new Edge(2,1,7),
new Edge(2,3,8),new Edge(2,4,3),new Edge(3,0,2),
new Edge(3,1,6),new Edge(3,2,8),new Edge(3,4,9),
new Edge(4,2,3),new Edge(4,3,9)};
AdjMatrixGraph<String> graph = new AdjMatrixGraph<String>(verices,edges);
System.out.println("带权无向图"+graph.toString());
System.out.println("插入顶点F,插入边(A,F,9),删除顶点C,删除边(D,E)");
int i = graph.insertVertex("F");
graph.insertEdge(0,i,9);
graph.insertEdge(i,0,9);
graph.removeVertex(2);
graph.removeEdge(2, 3);
graph.removeEdge(3, 2);
System.out.println(graph.toString());
}
}
关联矩阵
描述顶点与边之间的关联关系。如果图中 n 个顶点、e 条边,则为 n 行 e 列的矩阵,第 i 行第 j 列的元素,表征了第 i 个顶点是否与第 j 条边关联。每一列中只有两个元素不为0。(下面代码只是表示一下什么是关联矩阵)
package com.atguigu.prefect;
import java.util.Scanner;
public class InciMatrix {
public static void main(String[] args) {
Scanner s = new Scanner(System.in);
int n = s.nextint();
int m = s.nextint();
int[][] x = new int[n+1][m+1];
for (int j = 1; j <= m; j++) {
int a = s.nextint();
int b = s.nextint();
x[a][j] = 1;
x[b][j] = -1;
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= m; j++) {
System.out.print(x[i][j] + " ");
}
System.out.println();
}
}
}
邻接表
描述每个顶点的邻接关系。如果图中 n 个顶点,则为规模为 n 的向量。向量中的元素为列表,内容为该顶点所指向的邻接顶点。
package com.atguigu.prefect.form;
import java.util.*;
/**
* @anthor shkstart
* @create 2020-08-06 17:06
*/
public class LinkGraph {
Vertex[] vertex;
int[] parent;
//有参构造器
public LinkGraph(char[] vert,Edge[] edge) {
//读入顶点,并初始化
vertex = new Vertex[vert.length];
parent = new int[vert.length];
for (int i=0;i<vertex.length;i++) {
vertex[i]=new Vertex();
vertex[i].data=vert[i];
//顶点值
vertex[i].firstEdge=null;
//还没有邻接点,当然没有边了
}
//初始化边
for (int i=0;i<edge.length;i++) {
char start=edge[i].start;
char end=edge[i].end;
//获取顶点对应的序号
int p1=getPosition(start);
int p2=getPosition(end);
//1.把p2连接在以p1为头的链表中
Node node1=new Node();
node1.index=p2;
node1.weight=edge[i].weight;
linkedLast(p1,node1);
//2.因为是无向图,所以还需要把p1连接在以p2为头的链表中
Node node2=new Node();
node2.index=p1;
node2.weight=edge[i].weight;
linkedLast(p2,node2);
}
}
//获取某个顶点对应的序号
public int getPosition(char v) {
for (int i=0;i<vertex.length;i++) {
if(vertex[i].data==v) {
return i;
}
}
//不存在这样的顶点则返回-1
return -1;
}
//尾插法,将顶点连接到链表的尾巴
public void linkedLast(int index,Node node) {
if(vertex[index].firstEdge==null) {
vertex[index].firstEdge=node;
} else {
Node tmp=vertex[index].firstEdge;
while(tmp.nextNode!=null) {
tmp=tmp.nextNode;
}
tmp.nextNode=node;
}
}
//打印图
public void print() {
System.out.println("邻接表存储的图:");
for (int i=0;i<vertex.length;i++) {
System.out.print(vertex[i].data+"-->");
//如果存在邻接点
Node tmp=vertex[i].firstEdge;
while(tmp.nextNode!=null) {
System.out.print(vertex[tmp.index].data+"-->");
tmp=tmp.nextNode;
}
System.out.print(vertex[tmp.index].data);
System.out.println();
}
}
//深度优先搜索,从第一个顶点开始遍历
public void DFS() {
Boolean[] visited=new Boolean[vertex.length];
//默认为false;
int[] path=new int[vertex.length];
//记录遍历的顶点序号
int index=0;
//path[]的索引
Stack stack=new Stack();
visited[0]=true;
stack.push(0);
path[index++]=0;
while(!stack.isEmpty()) {
int v=getUnVisitedAdjVertex((Integer) stack.peek(),visited);
//如果不存在没有访问的邻接点,就出栈,原路返回
if(v==-1) {
stack.pop();
}
//否则,存在还没有访问过的邻接点,入栈,并标注已访问 else {
path[index++]=v;
//访问邻接点
visited[v]=true;
//标志已访问
stack.push(v);
//入栈
}
}
//打印DFS路径
System.out.println("DFS路径:");
for (int i=0;i<path.length;i++) {
System.out.print(vertex[path[i]].data+" ");
}
}
//查找某个点的还没有被访问的邻接点的序号
public int getUnVisitedAdjVertex(int v,Boolean[] visited) {
Node tmp=vertex[v].firstEdge;
//如果存在邻接点
while(tmp!=null) {
//并且邻接点还没有访问过,就返回该邻接点的序号
if(visited[tmp.index]==false) {
return tmp.index;
}
tmp=tmp.nextNode;
}
//不存在没有被访问的邻接点
return -1;
}
//广度优先搜索,从第一个顶点开始遍历
public void BFS() {
Boolean[] visited=new Boolean[vertex.length];
//默认为false;
int[] path=new int[vertex.length];
//记录遍历的顶点序号
int index=0;
//path[]的索引
Queue queue=new LinkedList<Integer>();
visited[0]=true;
queue.add(0);
path[index++]=0;
while(!queue.isEmpty()) {
int v=getUnVisitedAdjVertex((Integer) queue.peek(), visited);
//如果不存在没有访问的邻接点,就出队
if(v==-1) {
queue.remove();
}
//否则,存在还没有访问过的邻接点,入队,并标注已访问 else {
path[index++]=v;
//访问邻接点
visited[v]=true;
//标志已访问
queue.add(v);
//入队
}
}
//打印BFS路径
System.out.println("BFS路径:");
for (int i=0;i<path.length;i++) {
System.out.print(vertex[path[i]].data+" ");
}
}
//作为某个点的邻接点的顶点信息
class Node{
int index;
//顶点的序号
int weight;
//以该顶点为终点的边的权值
Node nextNode;
//指向下一个顶点
}
//输入的所有顶点的类型,是任意一条链表的起点
class Vertex{
char data;
//顶点值
Node firstEdge;
//指向第一条边
}
//边的类型
static class Edge{
char start;
//起点
char end;
//终点
int weight;
//边的权值
public Edge(char start,char end,int weight) {
this.start=start;
this.end=end;
this.weight=weight;
}
}
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
//顶点
Edge[] edges = { //边
// 起点 终点 权
new Edge('A', 'B', 12),
new Edge('A', 'F', 16),
new Edge('A', 'G', 14),
new Edge('B', 'C', 10),
new Edge('B', 'F', 7),
new Edge('C', 'D', 3),
new Edge('C', 'E', 5),
new Edge('C', 'F', 6),
new Edge('D', 'E', 4),
new Edge('E', 'F', 2),
new Edge('E', 'G', 8),
new Edge('F', 'G', 9),
}
;
LinkGraph graph=new LinkGraph(vexs,edges);
//打印图的邻接表
graph.print();
//深度优先搜索
graph.DFS();
System.out.println();
//广度优先搜索
graph.BFS();
}
}
死搬c++
enum EStatus {
UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD
}
enum VStatus {
UNDISCOVERED, DISCOVERED, VISITED
}
public class Edge<Te> {
Te data;
int weight;
EStatus status;
public Edge() {
}
public Edge(Te data, int weight) {
this.data = data;
this.weight = weight;
this.status = EStatus.UNDETERMINED;
}
public Te getData() {
return data;
}
public void setData(Te data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public EStatus getStatus() {
return status;
}
public void setStatus(EStatus status) {
this.status = status;
}
}
public class Vertex<Tv> {
private Tv data;
private int inDegree,outDegree;
private VStatus status;
private int dTime,fTime;
private int parent;
/*int priority;*/
//不知道如何设置
public Vertex() {
}
public Vertex(Tv data) {
this.data = data;
this.inDegree = 0;
this.outDegree = 0;
this.status = VStatus.UNDISCOVERED;
this.dTime = -1;
this.fTime = -1;
this.parent = -1;
}
public Tv getData() {
return data;
}
public void setData(Tv data) {
this.data = data;
}
public int getInDegree() {
return inDegree;
}
public void setInDegree(int inDegree) {
this.inDegree = inDegree;
}
public int getOutDegree() {
return outDegree;
}
public void setOutDegree(int outDegree) {
this.outDegree = outDegree;
}
public VStatus getStatus() {
return status;
}
public void setStatus(VStatus status) {
this.status = status;
}
public int getdTime() {
return dTime;
}
public void setdTime(int dTime) {
this.dTime = dTime;
}
public int getfTime() {
return fTime;
}
public void setfTime(int fTime) {
this.fTime = fTime;
}
public int getParent() {
return parent;
}
public void setParent(int parent) {
this.parent = parent;
}
}
public class Graph1<Tv,Te> implements GraphImpl<Tv,Te>{
private Vertex<Tv>[] V ;
private Edge<Te>[][] E ;
private int n;
private int e;
public Graph1() {
}
public Graph1(Vertex<Tv>[] v, Edge<Te>[][] e, int n, int e1) {
V = v;
E = e;
this.n = n;
this.e = e1;
}
@Override
public Tv vertex(int i) {
return V[i].getData();
}
@Override
public int inDegree(int i) {
return V[i].getInDegree();
}
@Override
public int outDegree(int i) {
return V[i].getOutDegree();
}
@Override
public int firstNbr(int i) {
return nextNbr(i,n);
//首个邻接顶点
}
@Override
public int nextNbr(int i,int j) {
while ((-1 < j) && !exists(i , --j));
return j;
}
@Override
public VStatus status(int i) {
return V[i].getStatus();
}
@Override
public int dTime(int i) {
return V[i].getdTime();
}
@Override
public int fTime(int i) {
return V[i].getfTime();
}
@Override
public int parent(int i) {
return V[i].getParent();
}
@Override
public int insert(Tv vertex) {
//插入顶点,返回编号
V[n] = (Vertex<Tv>) vertex;
n++;
return n-1;
}
@Override
public Tv remove(int i) {
Tv vBak = vertex(i);
for (int t = i - 1;t+1 < n;t++){
for (int j = 0; j < n; j++){
E[t][j] = E[t + 1][j];
E[j][t] = E[j][t + 1];
}
V[t] = V[t+1];
}
n--;
return vBak;
}
@Override
public Boolean exists(int i, int j) {
return (0 <= i) &&(i < n) && (0 <= j)&& (j < n) && (E[i][j] != null);
}
@Override
public EStatus status(int i, int j) {
return E[i][j].getStatus();
}
@Override
public Te edge(int i, int j) {
return E[i][j].getData();
}
@Override
public int weight(int i, int j) {
return E[i][j].getWeight();
}
@Override
public void insert(Te edge, int w, int i, int j) {
if (exists(i,j)) return;
E[i][j] = new Edge<Te>(edge, w);
e++;
int a = V[i].getInDegree();
int b = V[j].getOutDegree();
V[i].setInDegree(a+1);
V[j].setInDegree(b+1);
}
@Override
public Te remove(int i, int j) {
Te eBak = edge(i,j);
E[i][j] = null;
e--;
int a = V[i].getInDegree();
int b = V[j].getOutDegree();
V[i].setInDegree(a-1);
V[j].setInDegree(b-1);
return eBak;
}
public void dfs(int s){
int clock = 0;
int v = s;
do{
if (V[v].getStatus() == VStatus.UNDISCOVERED){
DFS(v,clock);
}
}
while (s != (v = (++v % n)));
}
public void DFS(int v,int clock){
//assert: 0 <= v < n
V[v].setdTime(++clock);
System.out.print(V[v].getData());
V[v].setStatus(VStatus.DISCOVERED);
for (int u = firstNbr(v);-1 < u;u = nextNbr(v,u)){
switch (V[u].getStatus()){
case UNDISCOVERED:
E[v][u].setStatus(EStatus.TREE);
V[u].setParent(v);
DFS(u,clock);
break;
case DISCOVERED:
E[v][u].setStatus(EStatus.BACKWARD);
break;
default:
E[v][u].setStatus(dTime(v) < dTime(u)?EStatus.FORWARD:EStatus.CROSS);
break;
}
V[v].setStatus(VStatus.VISITED);
V[v].setfTime(++clock);
}
}
public void bfs(int s){
int clock = 0;
int v = s;
do {
if (status(v) == VStatus.UNDISCOVERED){
BFS(v,clock);
}
}
while (s != (v = (++v % n)));
//这里逐一的方式
}
public void BFS(int v,int clock){
Queue<Integer> Q = new LinkedList<Integer>();
//引入辅劣队列
V[v].setStatus(VStatus.DISCOVERED);
Q.add(v);
while (!Q.isEmpty()){
v = Q.poll();
System.out.print(V[v].getData());
V[v].setdTime(++clock);
for (int u = firstNbr(v); -1 < u;u = nextNbr(v,u)){
if (status(u) == VStatus.UNDISCOVERED){
V[u].setStatus(VStatus.DISCOVERED);
Q.add(u);
E[v][u].setStatus(EStatus.TREE);
V[u].setParent(v);
} else {
E[v][u].setStatus(EStatus.CROSS);
}
V[v].setStatus(VStatus.VISITED);
}
}
}
}
测试
public void test2(){
Vertex<Character>[] v = new Vertex[10];
Edge<Integer>[][] e = new Edge[10][10];
v[0] = new Vertex<>('A');
v[1] = new Vertex<>('B');
v[2] = new Vertex<>('C');
v[3] = new Vertex<>('D');
v[4] = new Vertex<>('E');
int n = 5;
//点
int m = 6;
//边
e[0][4] = new Edge<Integer>(1,6);
e[1][0] = new Edge<Integer>(1,9);
e[1][2] = new Edge<Integer>(1,3);
e[2][0] = new Edge<Integer>(1,2);
e[2][3] = new Edge<Integer>(1,5);
e[3][4] = new Edge<Integer>(1,1);
Graph1<Character,Integer> graph = new Graph1<>(v,e,n,m);
/* graph.BFS(1,0);*/
System.out.println();
graph.DFS(1,0);
/*graph.dfs(0);*/
}
- 原理
广度优先搜索
https://blog.csdn.net/hehuanchun0311/article/details/80168109
原理
数据结构的简化分析:图遍历得到树,树遍历得到向量

广度优先搜索:对于访问始自顶点为 s 的图。
- 访问顶点 s 。
- 依次访问 s 所有尚未访问的邻接顶点。
- 依次访问上述顶点尚未访问的邻接顶点。
- 如此反复直至没尚未访问的邻接顶点。
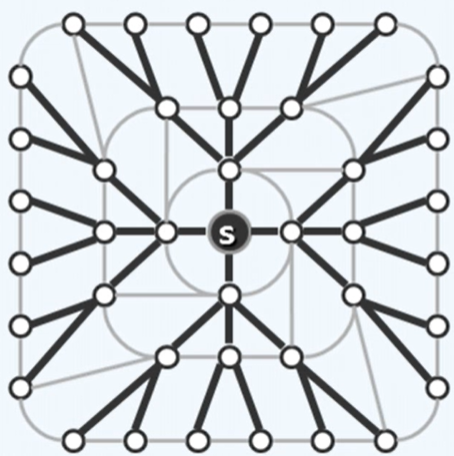
实例

实现
public void dfs(int s){
int clock = 0;
int v = s;
do{
if (V[v].getStatus() == VStatus.UNDISCOVERED){
DFS(v,clock);
}
}
while (s != (v = (++v % n)));
}
public void DFS(int v,int clock){
//assert: 0 <= v < n
V[v].setdTime(++clock);
System.out.print(V[v].getData());
V[v].setStatus(VStatus.DISCOVERED);
for (int u = firstNbr(v);-1 < u;u = nextNbr(v,u)){
switch (V[u].getStatus()){
case UNDISCOVERED:
E[v][u].setStatus(EStatus.TREE);
V[u].setParent(v);
DFS(u,clock);
break;
case DISCOVERED:
E[v][u].setStatus(EStatus.BACKWARD);
break;
default:
E[v][u].setStatus(dTime(v) < dTime(u)?EStatus.FORWARD:EStatus.CROSS);
break;
}
V[v].setStatus(VStatus.VISITED);
V[v].setfTime(++clock);
}
}
上层主函数bfs()的作用,正在于处理多个连通分量或可达分量并存的情况。具体地,在逐个 检查顶点的过程中,只要发现某一顶点尚未被发现,则意味着其所属的连通分量或可达分量尚未 触及,故可从该顶点出发再次启动BFS(),以遍历其所属的连通分量或可达分量。
深度优先搜索
原理
- 访问顶点 s 。
- 若 s 有尚未被访问的邻接,则任选其一 u ,递归执行深度优先搜索。
- 否则,返回上一顶点。

实现
public void bfs(int s){
int clock = 0;
int v = s;
do {
if (status(v) == VStatus.UNDISCOVERED){
BFS(v,clock);
}
}
while (s != (v = (++v % n)));
//这里逐一的方式
}
public void BFS(int v,int clock){
Queue<Integer> Q = new LinkedList<Integer>();
//引入辅劣队列
V[v].setStatus(VStatus.DISCOVERED);
Q.add(v);
while (!Q.isEmpty()){
v = Q.poll();
System.out.print(V[v].getData());
V[v].setdTime(++clock);
for (int u = firstNbr(v); -1 < u;u = nextNbr(v,u)){
if (status(u) == VStatus.UNDISCOVERED){
V[u].setStatus(VStatus.DISCOVERED);
Q.add(u);
E[v][u].setStatus(EStatus.TREE);
V[u].setParent(v);
} else {
E[v][u].setStatus(EStatus.CROSS);
}
V[v].setStatus(VStatus.VISITED);
}
}
}
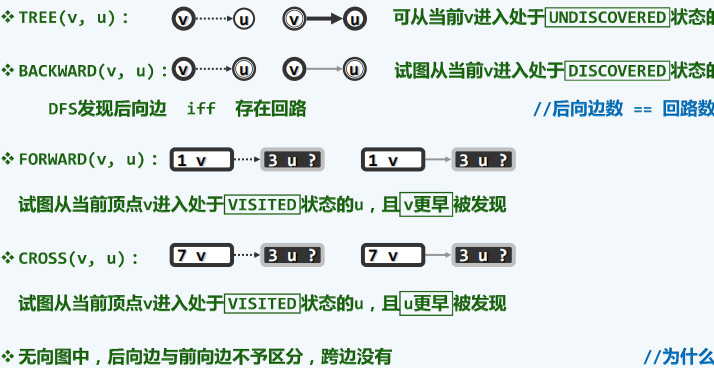
概念
-
活跃期
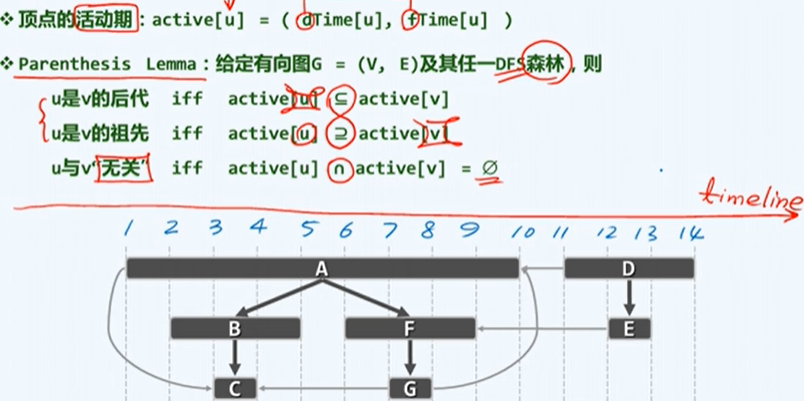
-
边的分类