树的特征
树是一种数据结构,它是n(n>=0)个节点的有限集。n=0时称为空树。n>0时,有限集的元素构成一个具有层次感的数据结构。
区别于线性表一对一的元素关系,树中的节点是一对多的关系。树具有以下特点:
- n>0时,根节点是唯一的,不可能存在多个根节点。
- 每个节点有零个至多个子节点;除了根节点外,每个节点有且仅有一个父节点。根节点没有父节点。
树的相关概念
树有许多相关的术语与概念,在学习树的结构之前,我们要熟悉这些概念:
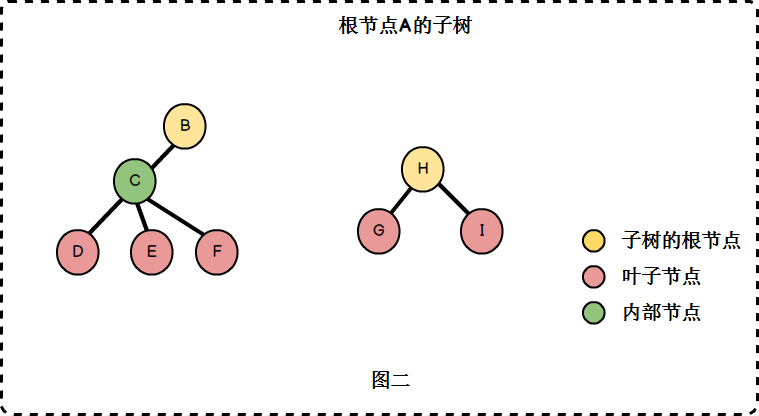
• 子树:除了根节点外,每个子节点都可以分为多个不相交的子树。(图二)
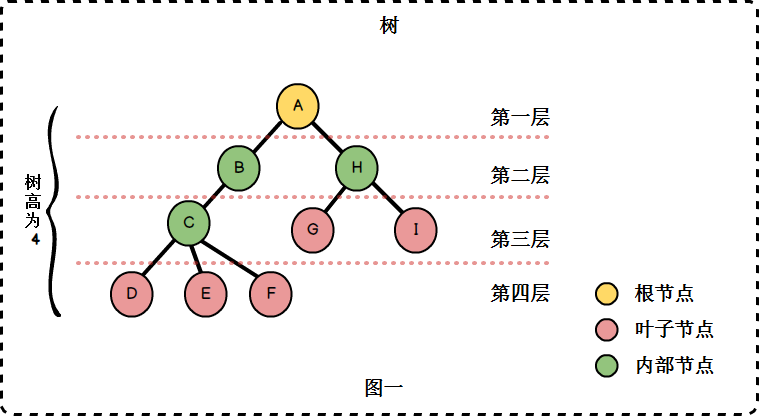
• 孩子与双亲:若一个结点有子树,那么该结点称为子树根的"双亲",子树的根是该结点的"孩子"。在图一中,B、H是A的孩子,A是B、H的双亲。
• 兄弟:具有相同双亲的节点互为兄弟,例如B与H互为兄弟。
• 节点的度:一个节点拥有子树的数目。例如A的度为2,B的度为1,C的度为3.
• 分支节点:除了叶子节点之外的节点,也即是度不为0的节点。
两种特殊的二叉树
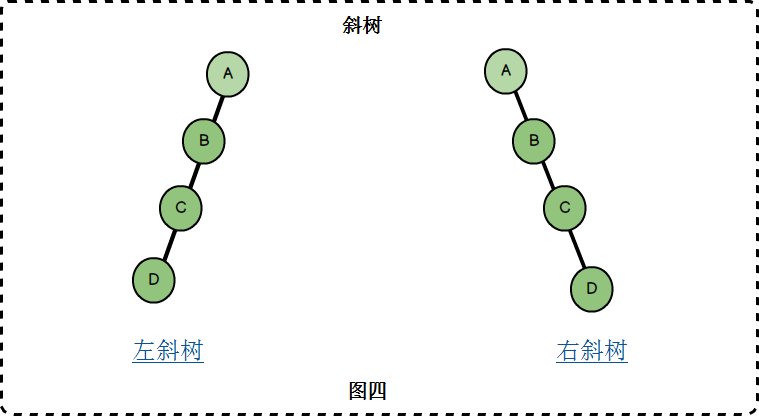
斜树
所有节点都只有左子树的二叉树叫做左斜树,所有节点都只有右子树的二叉树叫做右斜树。左斜树和右子树统称为斜树。
斜树已经退化成线性结构,二叉树在查找上表现出来优异性能在斜树得不到体现。
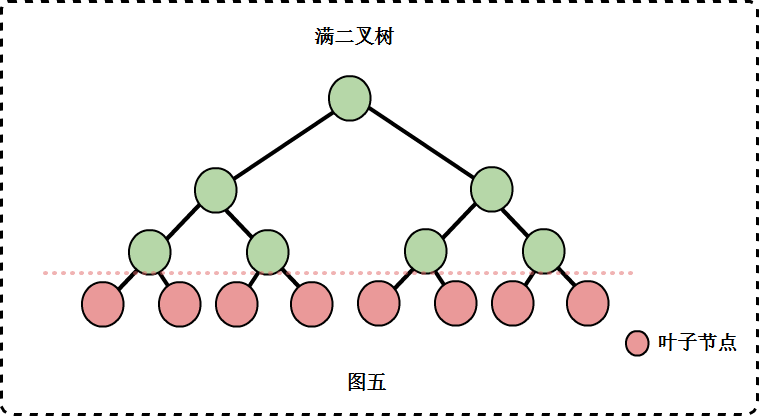
满二叉树
满二叉树要满足两个条件:
- 所有的节点都同时具有左子树和右子树。
- 所有的叶子节点都在同一层上。
在同样深度的二叉树中,满二叉树的节点数目是最多的,叶子数也是最多的。
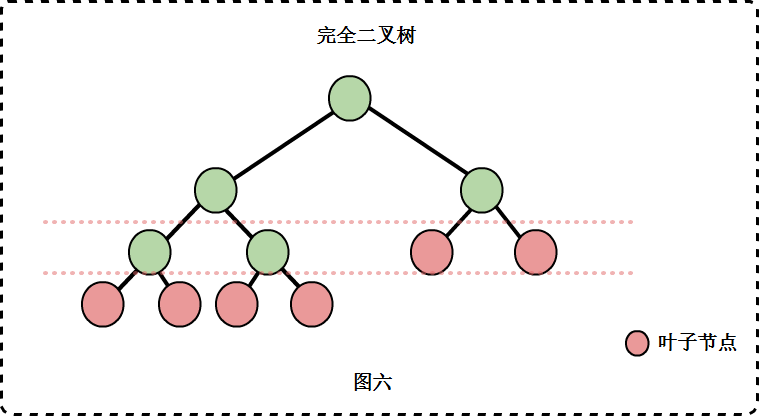
完全二叉树
完全二叉树(Complete Binary Tree) :若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
二叉树的存储结构
1. 二叉树的顺序存储

^代表不存在的结点。
对于右斜树,顺序存储结构浪费存储空间
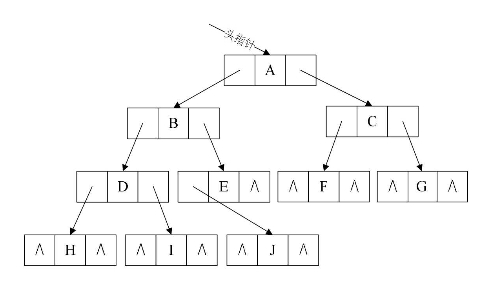
2. 二叉链表
链表每个结点包含一个数据域和两个指针域:

其中data是数据域,lchild和rchild都是指针域,分别指向左孩子和右孩子。