手动博客搬家: 本文发表于20181208 14:39:01, 原地址https://blog.csdn.net/suncongbo/article/details/84891710
哇它居然显示出图片来了……感动啊
题目链接:
https://www.lydsy.com/JudgeOnline/problem.php?id=4739
http://uoj.ac/problem/277
不难得出一个结论: 两圆之间最短路一定沿着圆的公切线走。然后得到如下算法:每两个圆之间作公切线(4条),如果一条公切线不穿过其他圆,就把这两个点(图论中的点)之间连上边,边权为切线长;同一圆上相邻两点连边,边权为圆上距离,然后S,T分别向每个圆作切线如果不和其他圆相交就连边。这样的话点数、边数是(O(n^2))级别的,使用Dijkstra算法求最短路即可。时间复杂度瓶颈在于对于一条边枚举每一个圆去check是否相交,总时间复杂度(O(n^3)). 奇迹般地能跑过。
下面重点讲解一下我是如何求两圆公切线以及点和圆的切线的:
先来说两圆公切线:因为两圆外离所以一定有(4)条公切线,(2)内(2)外。
考虑先把圆按半径从大到小排序,现在要从半径大的圆向半径小的圆作(4)条切线。
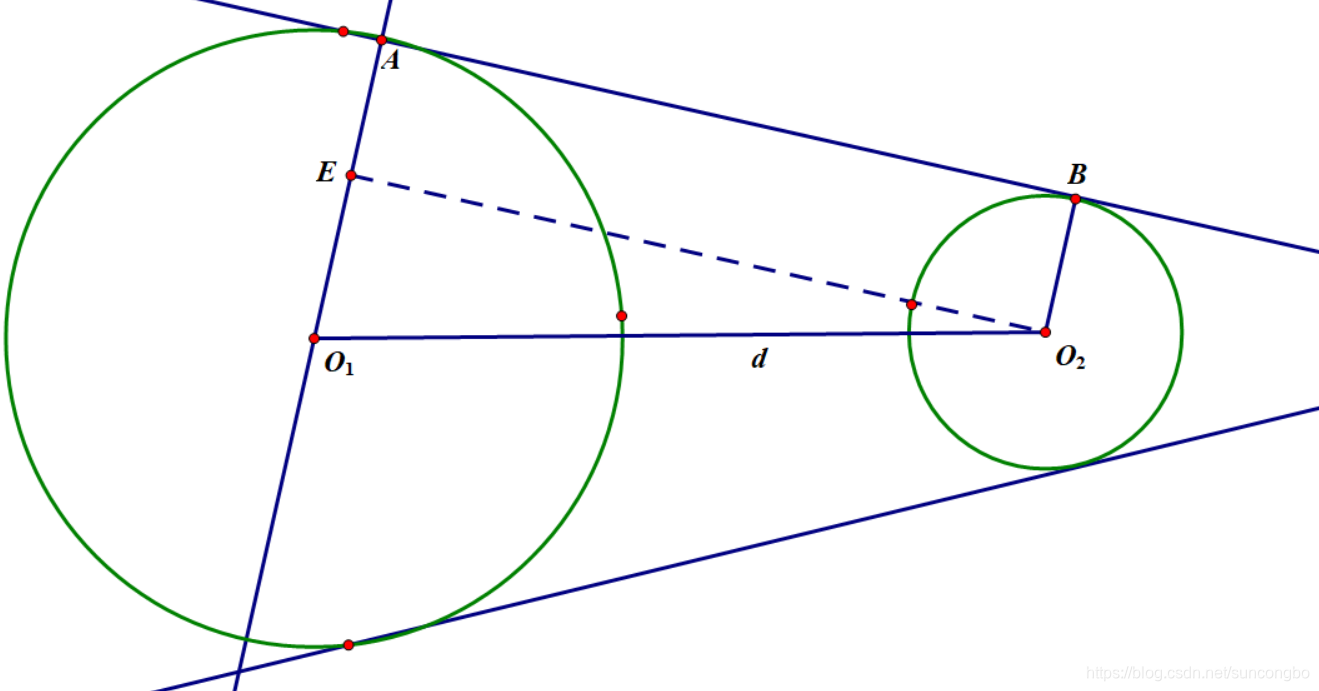
设两圆圆心(已知)分别为(O_1, O_2), 圆心的直线距离(O_1O_2=d), 半径分别为(r_1r_2), 一条外公切线为(AB)(未知)。
过(O_2)作(O_2Eperp AO_1)于(D), 则(AEO_2B)为矩形。(AE=BO_2=r_2), (EO_1=AO_1-AE=r_1-r_2), 又(O_1Eperp O_2E), 可用勾股定理算出切线长(AB=EO_2=sqrt{d^2-(r_1-r_2)^2}). 同时有(cos angle EO_1O_2=frac{r_1-r_2}{d}), 可利用acos函数算出(angle EO_1O_2)的值。然后求出向量(vec {OA}=frac{r_1}{d}vec v)即可,其中(vec v)为(vec {O_1O_2})逆时针旋转(angle EO_1O_2)的向量。
另外一条外公切线同理,把旋转度数取反即可。
代码如下:
Line tmp; double d = EuclidDist(a[i].o,a[j].o); Vector v; double ang; Point p1,p2;
//Out 1
ang = acos((a[i].r-a[j].r)/d); v = rotate(Vector(a[j].o-a[i].o),ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o+v*a[j].r;
tmp = Line(p1,p2);
//Out 2
v = rotate(Vector(a[j].o-a[i].o),-ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o+v*a[j].r;
tmp = Line(p1,p2);
对于两条内公切线,只要(EO_2=sqrt{d^2-(r_1+r_2)^2})然后计算即可。注意内公切线的向量是一加一减。
//In 1
ang = acos((a[i].r+a[j].r)/d); v = rotate(Vector(a[j].o-a[i].o),ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o-v*a[j].r;
tmp = Line(p1,p2);
//In 2
v = rotate(Vector(a[j].o-a[i].o),-ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o-v*a[j].r;
tmp = Line(p1,p2);
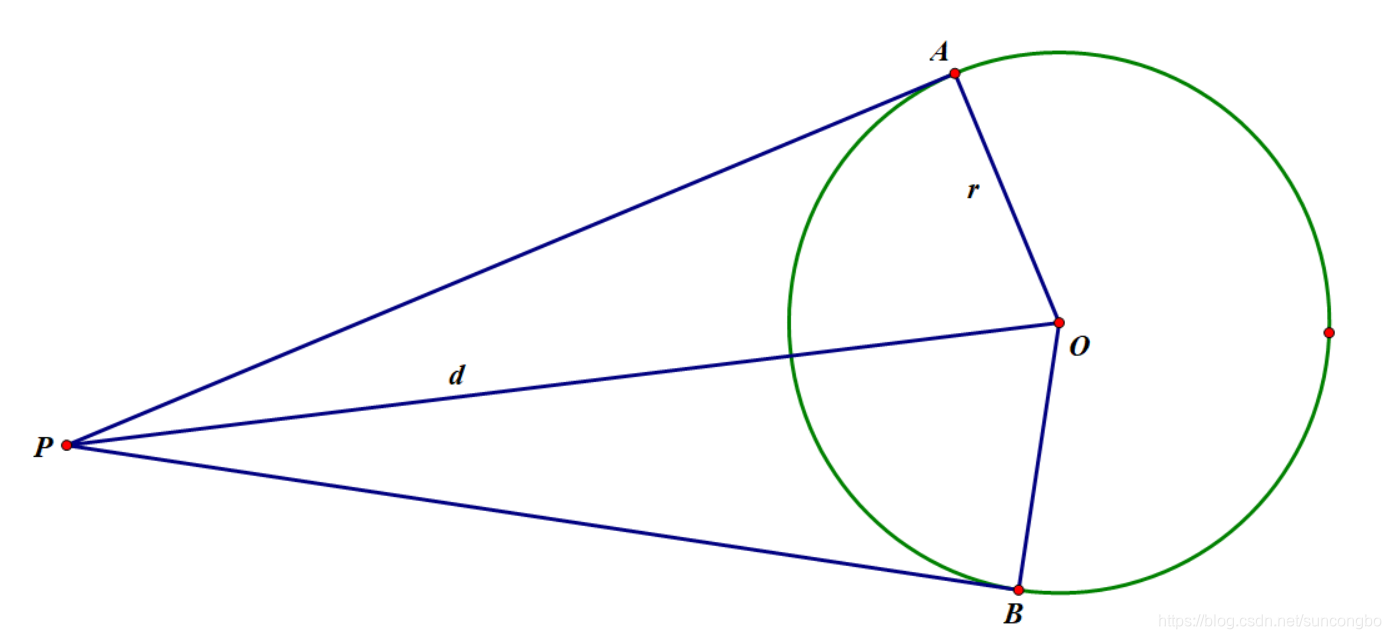
然后再来看过一点作圆的两条切线:
和刚才的做法类似,逆时针旋转向量(vec {OP}) (arcsin frac{r}{d})角即可。然后再除以(d)乘以(sqrt{d^2-r^2}).
代码如下:
Line tmp; double d; Vector v; Point p; double ang;
//1
d = EuclidDist(s1,a[i].o); ang = asin(a[i].r/d); v = rotate(Vector(a[i].o-s1),ang)/d;
p = s1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(s1,p);
//2
v = rotate(Vector(a[i].o-s1),-ang)/d;
p = s1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(s1,p);
另外的一些计算几何问题:
- 如何check: 对于一个圆判断当前线段到这个圆心的距离是否大于半径。点到线段的距离: 利用点积判断是否在端点两侧(和端点的夹角是否为钝角),如果不是利用叉积求点到直线的距离即可。
il double PointDisttoSegment(Line l,Point x)
{
Vector v1 = l.y-l.x,v2 = x-l.x,v3 = x-l.y;
if(dcmp(Dot(v1,v2))<0) return EuclidDist(x,l.x);
else if(dcmp(Dot(v1,v3))>0) return EuclidDist(x,l.y);
else return fabs(Cross(v2,v3))/EuclidDist(l.x,l.y);
}
- 如何求圆上距离
设圆半径为(r), 两点(AB)距离为(d), 则圆心角为( heta=2arcsin{frac{d}{2r}}).或者等于(arctan k_1-arctan k_2), (k_1, k_2)分别是(OA, OB)的斜率。两种计算方法均可,精度哪个更好未知。我使用了第二种。然后圆上距离就等于(r heta). (当时写成了(2pi r heta)调了好长时间) 注意特判负角度,不要走劣弧。
代码实现
7kb多一点……
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<vector>
#include<algorithm>
#include<map>
#include<queue>
#define llong long long
#define il inline
#define modinc(x) {if(x>=P) x-=P;}
using namespace std;
const int N1 = 502;
const double eps = 1e-15;
const int N = 2e6+2e3+2;
const int M = 4.25e6;
const double PI = 3.1415926535898;
const double INF = 1e9;
struct Point
{
double x,y;
Point() {}
Point(double _x,double _y) {x = _x,y = _y;}
double length() {return sqrt(x*x+y*y);}
bool operator ==(const Point &arg) const
{
return fabs(x-arg.x)<eps && fabs(y-arg.y)<eps;
}
bool operator <(const Point &arg) const
{
return x<arg.x || (x==arg.x && y<arg.y);
}
};
typedef Point Vector;
Point operator +(Point x,Vector y) {return Point(x.x+y.x,x.y+y.y);}
Point operator -(Point x,Vector y) {return Point(x.x-y.x,x.y-y.y);}
Vector operator *(Vector x,double y) {return Vector(x.x*y,x.y*y);}
Vector operator /(Vector x,double y) {return Vector(x.x/y,x.y/y);}
il double Cross(Vector x,Vector y) {return x.x*y.y-x.y*y.x;}
il double Dot(Vector x,Vector y) {return x.x*y.x+x.y*y.y;}
il int dcmp(double x) {return x<-eps ? -1 : (x>eps ? 1 : 0);}
il double EuclidDist(Point x,Point y) {return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));}
il Vector rotate(Vector x,double ang) {return Point(x.x*cos(ang)-x.y*sin(ang),x.x*sin(ang)+x.y*cos(ang));}
struct Circle
{
Point o; double r;
Circle() {}
Circle(Point _o,double _r) {o = _o,r = _r;}
bool operator <(const Circle &arg) const
{
return r<arg.r || (r==arg.r && o<arg.o);
}
};
struct Line
{
Point x,y;
Line() {}
Line(Point _x,Point _y) {x = _x,y = _y;}
};
struct Element
{
Line l; int id1,id2;
Element() {}
Element(Line _l,int _id1,int _id2) {l = _l,id1 = _id1,id2 = _id2;}
} q[M+2];
struct Edge
{
int v,nxt; double w;
} e[(M<<1)+2];
struct DijNode
{
int id; double dis;
DijNode() {}
DijNode(int _id,double _dis) {id = _id,dis = _dis;}
bool operator <(const DijNode &x) const
{
return dis>x.dis;
}
};
int fe[N+3];
double dis[N+3];
int vis[N+3];
priority_queue<DijNode> pq;
Circle a[N+3];
vector<Point> disc;
map<Point,int> mp;
vector<Point> belong[N1+3];
Point s1,t1,curo;
int n,tp,en;
il double PointDisttoSegment(Line l,Point x)
{
Vector v1 = l.y-l.x,v2 = x-l.x,v3 = x-l.y;
if(dcmp(Dot(v1,v2))<0) return EuclidDist(x,l.x);
else if(dcmp(Dot(v1,v3))>0) return EuclidDist(x,l.y);
else return fabs(Cross(v2,v3))/EuclidDist(l.x,l.y);
}
bool check(Line l,int x,int y)
{
for(int i=1; i<=n; i++)
{
if(i==x || i==y) continue;
double tmp = PointDisttoSegment(l,a[i].o);
if(dcmp(tmp-a[i].r)==-1) return false;
}
return true;
}
il void addedge(int u,int v,double w)
{
en++; e[en].v = v; e[en].w = w;
e[en].nxt = fe[u]; fe[u] = en;
}
il bool cmp(Circle x,Circle y) {return y<x;}
il bool cmp1(Point x,Point y)
{
Vector xx = x-curo,yy = y-curo;
return dcmp(atan2(xx.y,xx.x)-atan2(yy.y,yy.x))<0;
}
int getid(Point x) {return lower_bound(disc.begin(),disc.end(),x)-disc.begin()+1;}
double Dijkstra(int s,int t)
{
for(int i=1; i<=disc.size(); i++) dis[i] = INF;
pq.push(DijNode(s,0.0)); dis[s] = 0.0;
while(!pq.empty())
{
DijNode tmp = pq.top(); pq.pop(); int u = tmp.id;
if(tmp.dis!=dis[u]) continue;
if(vis[u]) continue;
vis[u] = true;
for(int i=fe[u]; i; i=e[i].nxt)
{
if(vis[e[i].v]==false && dcmp(dis[e[i].v]-dis[u]-e[i].w)==1)
{
dis[e[i].v] = dis[u]+e[i].w;
pq.push(DijNode(e[i].v,dis[e[i].v]));
}
}
}
return dis[t];
}
int main()
{
scanf("%lf%lf%lf%lf",&s1.x,&s1.y,&t1.x,&t1.y);
scanf("%d",&n);
for(int i=1; i<=n; i++)
{
scanf("%lf%lf%lf",&a[i].o.x,&a[i].o.y,&a[i].r);
}
sort(a+1,a+n+1,cmp);
tp = 0;
for(int i=1; i<=n; i++)
{
for(int j=i+1; j<=n; j++)
{
Line tmp; double d = EuclidDist(a[i].o,a[j].o); Vector v; double ang; Point p1,p2;
ang = acos((a[i].r-a[j].r)/d); v = rotate(Vector(a[j].o-a[i].o),ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o+v*a[j].r;
tmp = Line(p1,p2);
bool ok = check(tmp,i,j);
if(ok) {tp++; q[tp] = Element(tmp,i,j); belong[i].push_back(p1); belong[j].push_back(p2);}
v = rotate(Vector(a[j].o-a[i].o),-ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o+v*a[j].r;
tmp = Line(p1,p2);
ok = check(tmp,i,j);
if(ok) {tp++; q[tp] = Element(tmp,i,j); belong[i].push_back(p1); belong[j].push_back(p2);}
ang = acos((a[i].r+a[j].r)/d); v = rotate(Vector(a[j].o-a[i].o),ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o-v*a[j].r;
tmp = Line(p1,p2);
ok = check(tmp,i,j);
if(ok) {tp++; q[tp] = Element(tmp,i,j); belong[i].push_back(p1); belong[j].push_back(p2);}
v = rotate(Vector(a[j].o-a[i].o),-ang)/d;
p1 = a[i].o+v*a[i].r,p2 = a[j].o-v*a[j].r;
tmp = Line(p1,p2);
ok = check(tmp,i,j);
if(ok) {tp++; q[tp] = Element(tmp,i,j); belong[i].push_back(p1); belong[j].push_back(p2);}
}
}
for(int i=1; i<=n; i++)
{
Line tmp; double d; Vector v; Point p; double ang;
d = EuclidDist(s1,a[i].o); ang = asin(a[i].r/d); v = rotate(Vector(a[i].o-s1),ang)/d;
p = s1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(s1,p);
bool ok = check(tmp,0,i);
if(ok) {tp++; q[tp] = Element(tmp,0,i); belong[i].push_back(p);}
v = rotate(Vector(a[i].o-s1),-ang)/d;
p = s1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(s1,p);
ok = check(tmp,0,i);
if(ok) {tp++; q[tp] = Element(tmp,0,i); belong[i].push_back(p);}
d = EuclidDist(t1,a[i].o); ang = asin(a[i].r/d); v = rotate(Vector(a[i].o-t1),ang)/d;
p = t1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(p,t1);
ok = check(tmp,i,0);
if(ok) {tp++; q[tp] = Element(tmp,i,0); belong[i].push_back(p);}
v = rotate(Vector(a[i].o-t1),-ang)/d;
p = t1+v*sqrt(d*d-a[i].r*a[i].r);
tmp = Line(p,t1);
ok = check(tmp,i,0);
if(ok) {tp++; q[tp] = Element(tmp,i,0); belong[i].push_back(p);}
}
for(int i=1; i<=tp; i++)
{
disc.push_back(q[i].l.x); disc.push_back(q[i].l.y);
}
disc.push_back(s1); disc.push_back(t1);
sort(disc.begin(),disc.end());
disc.erase(unique(disc.begin(),disc.end()),disc.end());
for(int i=0; i<disc.size(); i++)
{
mp[disc[i]] = i+1;
}
for(int i=1; i<=n; i++)
{
curo = a[i].o;
sort(belong[i].begin(),belong[i].end(),cmp1);
belong[i].erase(unique(belong[i].begin(),belong[i].end()),belong[i].end());
if(belong[i].size()==1) continue;
for(int j=0; j<belong[i].size(); j++)
{
int prv = j-1; if(prv==-1) prv = belong[i].size()-1;
Vector v1 = belong[i][j]-a[i].o,v2 = belong[i][prv]-a[i].o;
double ang = fabs(atan2(v1.y,v1.x)-atan2(v2.y,v2.x));
if(dcmp(ang-PI)==1) ang = 2.0*PI-ang;
addedge(mp[belong[i][j]],mp[belong[i][prv]],ang*a[i].r);
addedge(mp[belong[i][prv]],mp[belong[i][j]],ang*a[i].r);
}
}
for(int i=1; i<=tp; i++)
{
addedge(mp[q[i].l.x],mp[q[i].l.y],EuclidDist(q[i].l.x,q[i].l.y));
addedge(mp[q[i].l.y],mp[q[i].l.x],EuclidDist(q[i].l.x,q[i].l.y));
}
if(check(Line(s1,t1),0,0))
{
addedge(mp[s1],mp[t1],EuclidDist(s1,t1));
addedge(mp[t1],mp[s1],EuclidDist(s1,t1));
}
double ans = Dijkstra(mp[s1],mp[t1]);
printf("%.1lf
",ans);
return 0;
}