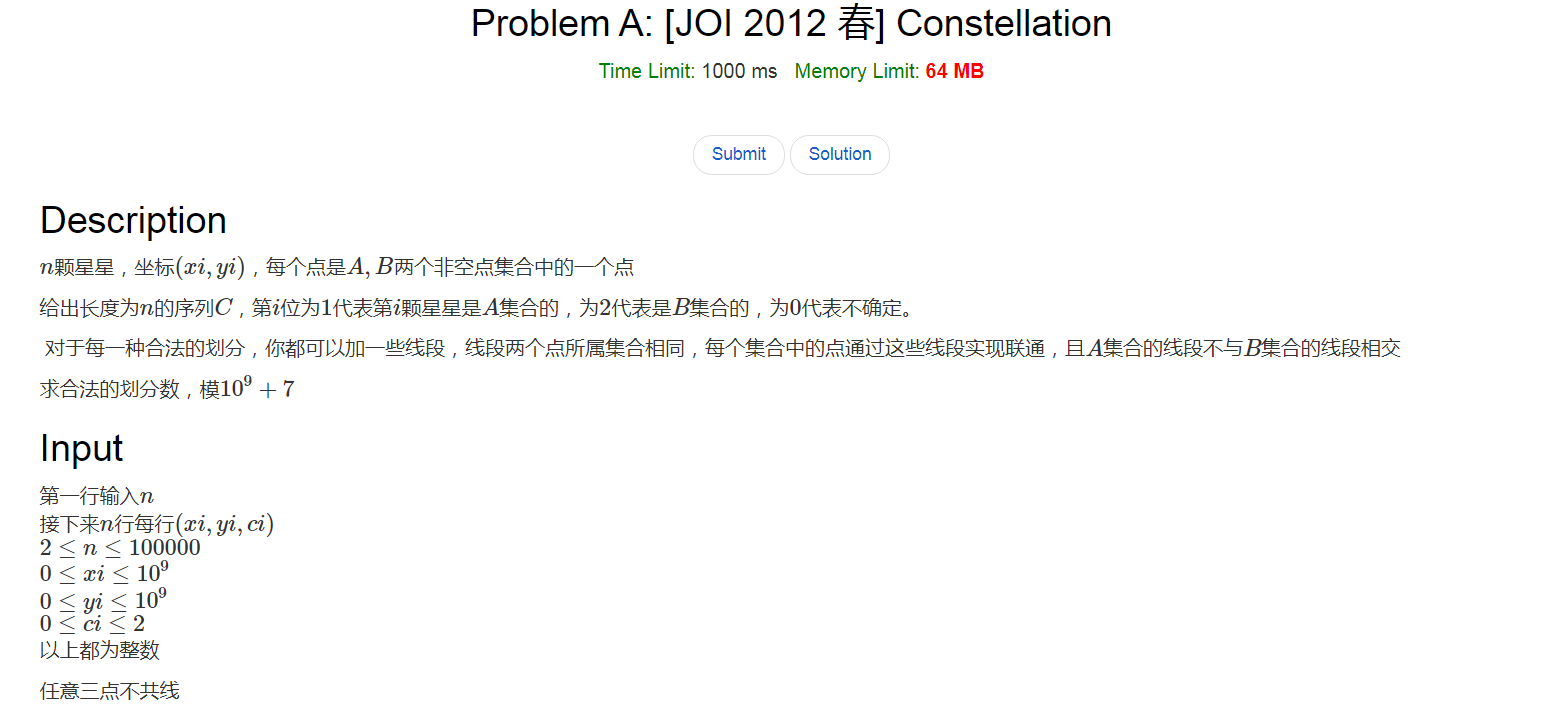
题意

题解
神仙结论题。
结论: 一个点集合法当且仅当其凸包上的两种颜色点分别连续。
证明:
必要性显然。
充分性: 考虑对于一个不同色三角形(ABC),不妨设点(A)为白点,点(B,C)为黑点。若形内无白点,则随便连,显然成立。若形内有白点,则任取一白点(S), 对三角形(SBC,BAS,CAS)内部的点分别连边(递归构造),最后连接(SA).
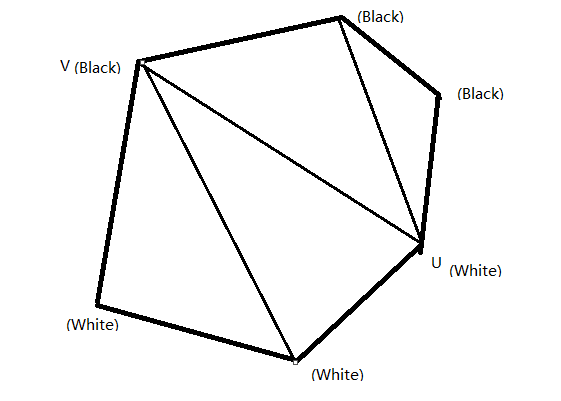
再考虑一个凸包,设在逆时针方向上最后一个白点是(U), 最后一个黑点是(V), 则连接(UV), 把凸包剖成两个部分,一部分只有(V)是黑,一部分只有(U)是白。然后进行如图所示三角剖分,每个三角形内连上即可。
知道了结论,这题就很简单了。
勿忘非空。
代码
#include<bits/stdc++.h>
#define llong long long
using namespace std;
const int N = 1e5;
const int P = 1e9+7;
struct Point
{
llong x,y; int c,id;
Point() {}
Point(int _x,int _y) {x = _x,y = _y;}
} a[N+3],ch[N+3];
bool f[N+3];
Point operator -(Point x,Point y) {return Point(x.x-y.x,x.y-y.y);}
llong Cross(Point x,Point y) {return x.x*y.y-x.y*y.x;}
int n,sz;
bool cmp_ang(Point x,Point y) {return Cross(x-a[1],y-a[1])>0;}
int main()
{
scanf("%d",&n);
for(int i=1; i<=n; i++) scanf("%lld%lld%d",&a[i].x,&a[i].y,&a[i].c);
for(int i=2; i<=n; i++) {if(a[i].x<a[1].x||(a[i].x==a[1].x&&a[i].y<a[1].y)) {swap(a[i],a[1]);}}
sort(a+2,a+n+1,cmp_ang);
for(int i=1; i<=n; i++) a[i].id = i;
sz = 1; ch[1] = a[1];
for(int i=2; i<=n; i++)
{
while(sz>=2 && Cross(ch[sz]-ch[sz-1],a[i]-ch[sz-1])<0) {sz--;}
sz++; ch[sz] = a[i];
}
// printf("ch: "); for(int i=1; i<=sz; i++) printf("(%lld,%lld) ",ch[i].x,ch[i].y); puts("");
int mx1 = 0,mn1 = n,mx2 = 0,mn2 = n; llong ans;
for(int i=1; i<=sz; i++)
{
if(ch[i].c==1) {mx1 = max(mx1,i),mn1 = min(mn1,i);}
else if(ch[i].c==2) {mx2 = max(mx2,i),mn2 = min(mn2,i);}
}
// printf("sz=%d mn1=%d mx1=%d mn2=%d mx2=%d
",sz,mn1,mx1,mn2,mx2);
if(mx1<mn1 && mx2<mn2)
{
ans = (1ll*sz*sz-sz+2ll)%P;
}
else if(mx1<mn1) //only 2
{
ans = 1ll;
for(int i=mn2+1,j=0; i<=mn2+sz; i++)
{
int ii = i>sz?i-sz:i;
if(ch[ii].c==0) {j++;}
else {ans += 1ll*j*(j+1ll)/2ll; j = 0;}
}
ans %= P;
}
else if(mx2<mn2) //only 1
{
ans = 1ll;
for(int i=mn1+1,j=0; i<=mn1+sz; i++)
{
int ii = i>sz?i-sz:i;
if(ch[ii].c==0) {j++;}
else {ans += 1ll*j*(j+1ll)/2ll; j = 0;}
}
ans %= P;
}
else
{
if(mn1>mn2)
{
for(int i=mn1; i<=mx1; i++)
{
if(ch[i].c==2) {puts("0"); return 0;}
}
int l = -1,r = -1;
for(int i=mx1; ch[i].c!=2; i=(i==sz?1:i+1))
{
l++;
}
for(int i=mn1; ch[i].c!=2; i=(i==1?sz:i-1))
{
r++;
}
ans = 1ll*(l+1ll)*(r+1ll)%P;
}
else
{
for(int i=mn2; i<=mx2; i++)
{
if(ch[i].c==1) {puts("0"); return 0;}
}
int l = -1,r = -1;
for(int i=mx2; ch[i].c!=1; i=(i==sz?1:i+1))
{
l++;
}
for(int i=mn2; ch[i].c!=1; i=(i==1?sz:i-1))
{
r++;
}
ans = 1ll*(l+1ll)*(r+1ll)%P;
}
}
for(int i=1; i<=sz; i++)
{
f[ch[i].id] = true;
}
int cnt1 = 0,cnt2 = 0;
for(int i=1; i<=n; i++)
{
if(f[i]==false && a[i].c==0) {ans=(ans<<1)%P;}
if(a[i].c==1) cnt1++;
if(a[i].c==2) cnt2++;
}
if(cnt1==0) {ans--;} if(cnt2==0) {ans--;}
ans = (ans+P)%P;
printf("%lld
",ans);
return 0;
}