题目地址:https://www.acwing.com/problem/content/244/
题目描述:
给定一个长度为N的数列A,以及M条指令,每条指令可能是以下两种之一:
1、“C l r d”,表示把 A[l],A[l+1],…,A[r] 都加上 d。
2、“Q l r”,表示询问 数列中第 l~r 个数的和。
对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数N,M。
第二行N个整数A[i]。
接下来M行表示M条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤1e5,
|d|≤10000,
|A[i]|≤1000000000
题解:这是对树状数组的更深一步的扩展:区间加、区间求和。所以需要解决两个问题:区间加、区间和。区间加比较容易,直接差分就可以。至于区间和我们可以想办法求出原序列a的前缀和表示方法,b是原序列的差分数组
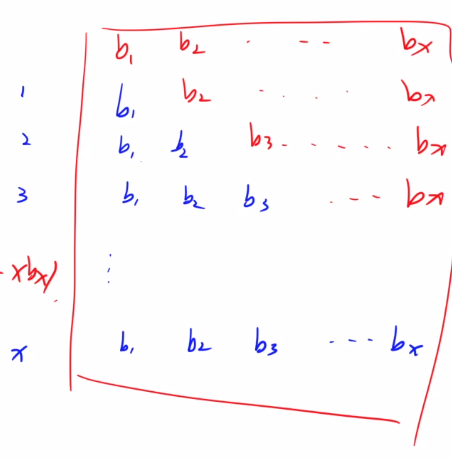
这张图片中的蓝色的,每一行蓝色的和都是一个元素a,分别表示a[1].....a[x].所以我们只需要求出a的前缀和,那么对于区间的和就显而易见了。至于图中的红色是一个填补的作用,我们可以知道a的前缀和就是蓝色+红色再减去红色。首先,蓝色+红色=a[x]*(x+1),而a[x]可以由差分数组b的前缀和求出。红色其实是i*b[i]的前缀和。所以a的前x的和S[x]=b[i]的前缀和*(x+1)-i*b[i]的前缀和。所以查询[l,r]=S[r]-S[l-1]
AC代码:
#include<iostream> #include<cstring> using namespace std; const int N=1e5+10; #define lowbit(x) (x&(-x)) #define ll long long int ll a[N]={0},b[N]={0},c[2][N]={0},n,m; void add(int k,int x,ll d){ while(x<=n){ c[k][x]+=d; x+=lowbit(x); } } ll sum(int k,int x){ ll sum=0; while(x>0){ sum+=c[k][x]; x-=lowbit(x); } return sum; } ll prefix_sum(int x){ return sum(0,x)*(x+1)-sum(1,x); } int main(){ cin>>n>>m; memset(c,0,sizeof(c)); ll now=0,x; for(int i=1;i<=n;i++){ cin>>x; a[i]=x-now; now=x; } for(int i=1;i<=n;i++){ add(0,i,a[i]);//差分数组a[i] add(1,i,i*a[i]);//差分数组i*a[i] } char ch; ll l,r,d; while(m--){ cin>>ch; if(ch=='C'){ cin>>l>>r>>d; add(0,l,d); add(0,r+1,-d); add(1,l,l*d); add(1,r+1,(r+1)*(-d)); } else { cin>>l>>r; cout<<(prefix_sum(r)-prefix_sum(l-1))<<endl; } } return 0; }
写于:2020/8/26 17:27