2.6逻辑回归与交叉熵
之前的线性回归预测的是一个连续值,而逻辑回归预测的是“是”和“否”的回答。
需要用到一个sigmoid激活函数,系那个结果映射到0到1之间,就可以将结果堪称一个概率值,当小于0.5认为是一个负面回答,否则认为是一个正面回答。
逻辑回归的损失函数不能使用线性回归的损失函数均方差,这是因为如果真实结果是正面回答也就是1,而预测的是0.3,这样所得到的均方差都是比较小的,因为每次的差值都是小于1,那么导致最后的训练次数需要增多,毕竟,损失函数的结果非常小。
对于分类问题,一般使用交叉熵巡视函数,交叉熵会给出一个更大的“损失”。
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。假设概率分布p为期望输出,概率分布q为实际输出,H(p.q)为交叉熵
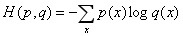
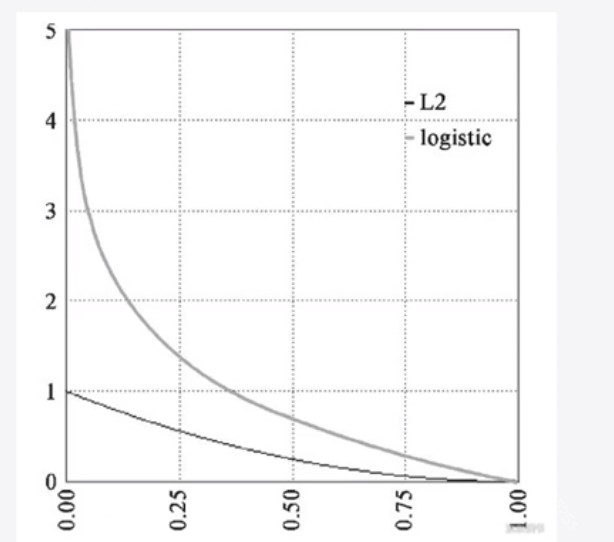
图22-14
从图2-14中我们可以看出当靠近0的时候,L2也即是最小二乘法损失比较小,而sigmoid的损失比较大。交叉熵损失放大了这种概率分布之间的损失。