希尔排序法及其js实现

希尔(Shell)排序又称为缩小增量排序，它是一种插入排序。它是直接插入排序算法的加强版。

希尔增量：

　　希尔增量是指希尔提出了一种冲破二次时间屏障的算法。

　　Donald Shell 提出了一种冲破二次时间屏障的算法Shellsort（希尔排序），在希尔排序中希尔给出了一组增量序列：ht = N / 2, h[k] = h[k+1] / 2，即 {N/2, (N / 2)/2, ..., 1}，这个序列就叫做希尔增量。这个是编写希尔排序时最常用的序列，但却不是最好的。其余的增量序列还有Hibbard：{1, 3, ..., 2^k-1}，Sedgewick：{1, 5, 19, 41, 109...}该序列中的项或者是9*4^i - 9*2^i + 1或者是4^i - 3*2^i + 1。使用不同的增量对希尔排序的时间复杂度的改进将不一样，甚至一点小的改变都将引起算法性能剧烈的改变。

希尔排序的基本思想是：

把记录按步长 gap 分组，对每组记录采用直接插入排序方法进行排序。
随着步长逐渐减小，所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

我们来通过演示图，更深入的理解一下这个过程。

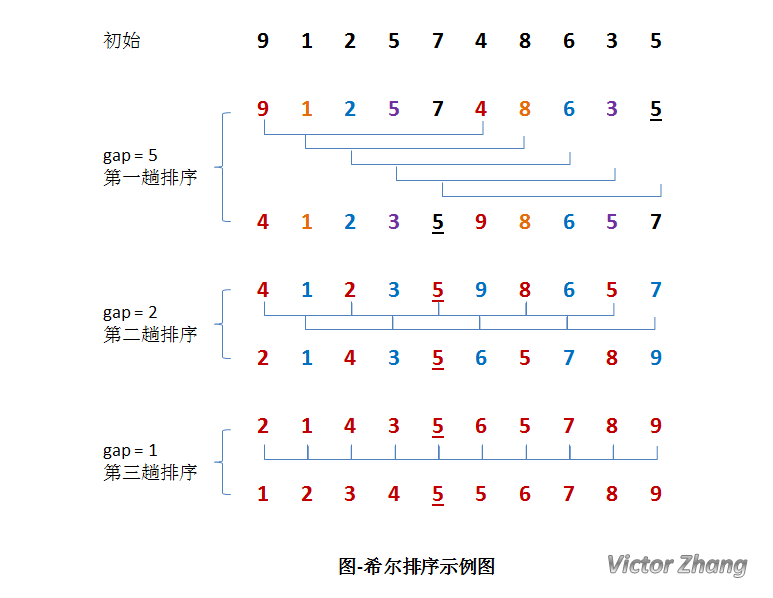
在上面这幅图中：

初始时，有一个大小为 10 的无序序列。

在第一趟排序中，我们不妨设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。

接下来，按照直接插入排序的方法对每个组进行排序。

在第二趟排序中，我们把上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为 2 组。

按照直接插入排序的方法对每个组进行排序。

在第三趟排序中，再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为 1 的元素组成一组，即只有一组。

按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

需要注意一下的是，图中有两个相等数值的元素 5 和 5 。我们可以清楚的看到，在排序过程中，两个元素位置交换了。

所以，希尔排序是不稳定的算法。

js实现

        let dat=[5, 8, 10, 3, 2, 18, 17, 9];
        function insertSort(data) {
            var gap=Math.floor(data.length/2);
        var  temp;//用于存储需要插入的数据
        //注意i从gap开始，因为以data[0]为基准数,j=i-1
        while(gap>=1){
            for(let i=gap;i<data.length;i++){
            temp=data[i]; //将第i个数保存，以供之后插入合适位置使用
            // 因为前i-1个数都是从小到大的有序序列，只要当前比较的数(data[j-1])比temp大，就把这个数后移一位
            for(var j=i-gap;j>=0&&data[j]>temp;j=j-gap){   //这块j得用var声明，因为在for循环之外的作用域还要用j
                data[j+gap]=data[j];
            }
            data[j+gap]=temp;//将temp插入合适的位置
        }
        gap=Math.floor(gap/2);
    } 
    return data;  
}  

var sortedData=insertSort(dat);
console.log(sortedData);