| 组员 | 任务分配 |
|---|---|
| 孙晴晴 | 原型设计,游戏路线输出等 |
| 李佳乐 | AI设计,图片分割,调换图片等 |
GitHub链接:https://github.com/031804126/pairWork
队友的博客链接:https://www.cnblogs.com/Jelor/p/13836371.html
队友的GitHub链接:https://github.com/031804120/huarongdao
part one:原型设计
(一): 设计说明
1、html 文件用于整个游戏界面的布局;整个布局分为两个部分,一个是游戏菜单部分,就是最上面蓝色背景部分;另一部分是游戏内容区域,包含左右两个部分,左边是进行游戏的区域,右边是提示图片;
2、整个html文件采用flex布局,所以css文件里需要使用flex布局实现html文件的界面需求;总体布局采用列方向排列子元素;然后每一列中采用行方向排列子元素;总体布局示意图如下:
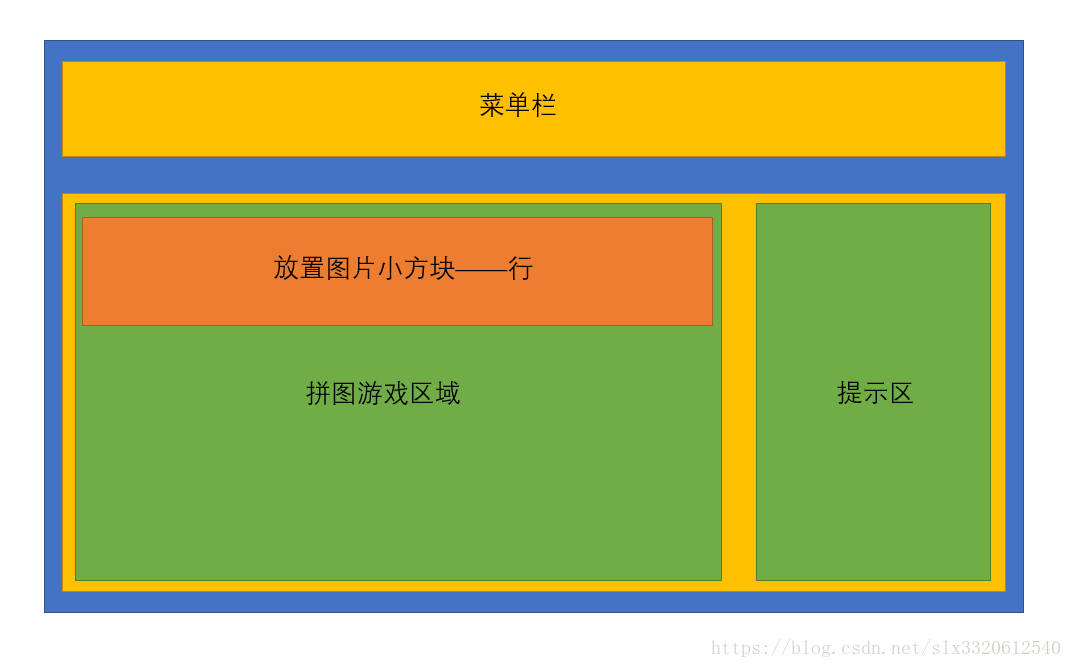
模型图:

当点击提示的时候,程序会自动进行操作,直到完成拼图。
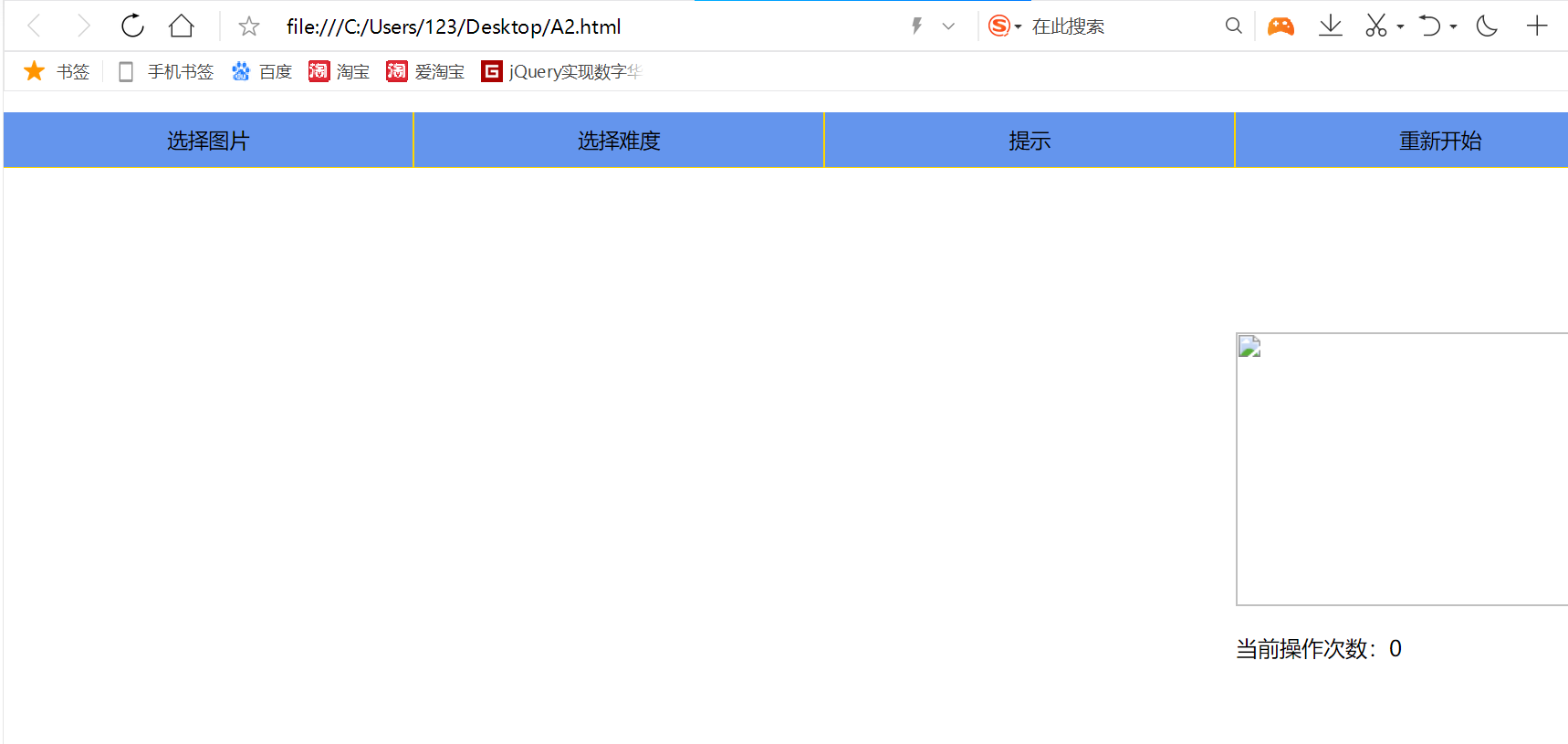
实际开发时的效果如图:
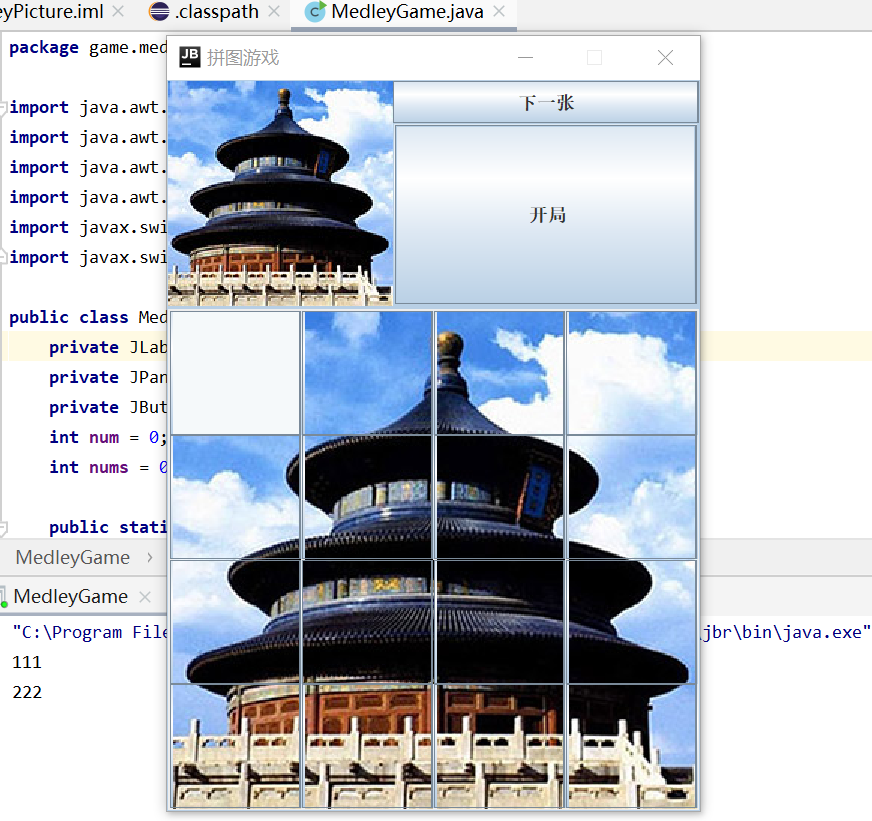
点击开局即可开始游戏,点击下一张更换图片
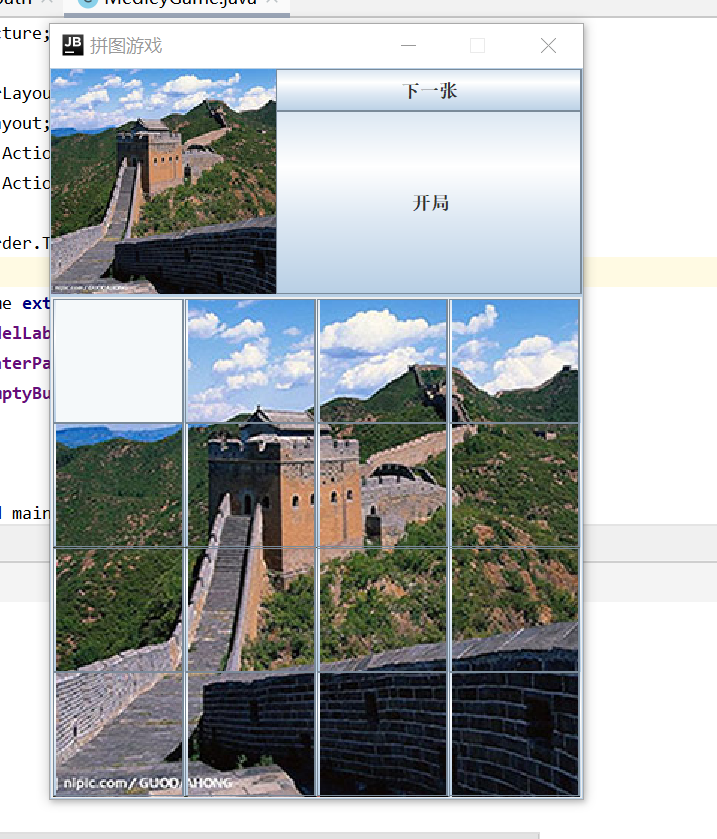
操作时在下面即时输出操作路径
(二):开发工具:JavaScript、prototype
(三):结对的初衷是我们两个在同一宿舍,这样有问题方便即时交流。

(四)遇到的困难;模型图不太稳定,有时候会加载不出来,如图所示
或者是图片的按钮功能实现不了。
解决尝试:曾尝试修改部分代码或是更换打开的浏览器,以及重启电脑,但是问题还是没有解决。
收获:刚开始都不太懂原型设计是什么意思,以为只是描绘出游戏界面,走了很多弯路,弄懂真正的要求后,赶紧学习了JavaScript相关知识,也算是又掌握了新的知识吧。
part two:AI与原型设计实现
(一)AI部分
网络接口我们是直接用postman,比较方便,不用再编码。
AI部分我们采用了BFS广度优先搜索与A*算法
1、BFS广度优先搜索:其基本思想是优先从当前节点的邻居节点开始搜索,如果搜索不到,再搜索邻居的邻居。其在算法设计的时候,主要考虑节点的标记和邻居的保存。

2、A算法
A算法最为核心的部分,就在于它的一个估值函数的设计上:f(n)=g(n)+h(n)
其中f(n)是每个可能试探点的估值,它有两部分组成:一部分,为g(n),它表示从起始搜索点到当前点的代价(通常用某结点在搜索树中的深度来表示),另一部分,即h(n),它表示启发式搜索中最为重要的一部分,即当前结点到目标结点的估值。
用一个实例来说明:

过程:
①.初始化列表open和close,将起点元素存入open中,其中open用来保存探索列表而close则保存访问列表
②.如果open不为空,则取出open的第一个元素,并转到2;如果open为空,则结束
③.取出第一个元素后,删除open中和第一个元素有相同目的节点的元素,并且对其邻居进行遍历,如果该邻居不在close中,则存入open中
④.对open中的节点按照f(n)大小进行升序排序,并转到2
代码实现:

关键代码
`
# 计算当前点到目标点的距离, 即A*算法的估计函数
def cal_distance(idxs):
distance = 0
for i in range(len(idxs)):
if idxs[i] == 0:
continue
distance += abs(i // width - (idxs[i] - 1) // width) + abs(i % width - (idxs[i] - 1) % width)
return distance
`
`
# BFS搜索
while not pq.empty():
# 获取中间值
_, board, position, step, move_str, board_roads = pq.get()
# 最终结果返回, 循环停止条件
if board == board_end:
return step, move_str, board_roads
# BFS遍历上下左右的相邻结点
for idx in (-width, width, -1, 1):
# wsad字母 对应 上下左右 的按钮
id2button = {-1:"a", 1:"d", -"w", "s"}
# 下一个需要遍历的点
neighbor = position + idx
# 不是相邻点的跳过
if abs(neighbor // width - position // width) + abs(neighbor % width - position % width) != 1:
continue
# 遍历上下左右符合边界条件的相邻数字(图片)
if 0 <= neighbor < width * hight:
board_mid = list(board)
# 交换, 即移动0(即空图片)
board_mid[position], board_mid[neighbor] = board_mid[neighbor], board_mid[position]
board_new = tuple(board_mid)
if board_new not in visited:
visited.add(board_new)
pq.put([cal_distance(board_new) + step + 1, board_new, neighbor, step + 1,
move_str + id2button[idx], board_roads + [board_mid]])
# 遍历整个循环都没有,则无解,返回-1
return -1, None, None
`
路线输出:
`
for idx in (-width, width, -1, 1):
# wsad字母 对应 上下左右 的按钮
id2button = {-1: "a", 1: "d", - "w", "s"}
# 下一个需要遍历的点
neighbor = position + idx
# 不是相邻点的跳过
if abs(neighbor // width - position // width) + abs(neighbor % width - position % width) != 1:
continue
# 遍历上下左右符合边界条件的相邻数字(图片)
if 0 <= neighbor < width * hight:
board_mid = list(board)
# 交换, 即移动0(即空图片)
board_mid[position], board_mid[neighbor] = board_mid[neighbor], board_mid[position]
board_new = tuple(board_mid)
if board_new not in visited:
visited.add(board_new)
pq.put([cal_distance(board_new) + step + 1, board_new, neighbor, step + 1,
move_str + id2button[idx], board_roads + [board_mid]])
# 遍历整个循环都没有,则无解,返回-1
return -1, None, None
`
类图:


原型设计部分分为更换游戏图片、难度选择、记录操作步数、小方块的填充、判断游戏结束、交换小方块图片、数据存储、重新开局以及提示功能几个模块,每个模块都构造了相应地函数实现。
重要代码:
`
/**
* 提示的点击函数,从操作栈里弹出一个函数,然后调用即可复原
*/
function onTips(){
let doFunction=operateStack.pop();
if(doFunction){
doFunction();
}//实际上,操作栈为空的时候,游戏也就结束了
}
`
`
/**
* 该函数起到洗牌操作,但是不展示“特效”,仅仅在数据上实现洗牌;
* 该洗牌算法保证了游戏一定有解,但是比较愚蠢,有可能左移晚就右移,实际上也应该可以处理
* 但是由于尚未实现
* @returns {Array}图片位置信息数组
*/
function getOpeningPositions(){
let positions=[];
operateStack=[];
for(let y=0;y<difficulty;y++){
for(let x=0;x<difficulty;x++){
positions[y*difficulty+x]=new Position(x,y);
}
}//完成顺序填充
let currentEmptyX=difficulty-1;
let currentEmptyY=difficulty-1;//记录空块位置信息
let emptyPositionId=currentEmptyX+currentEmptyY*difficulty;
let moveNum=5*difficulty;//生成移动次数
let tempPosition;
let targetPositionId;
let directionNum;
let doExchange=false;//是否需要执行交换
for(let i=0;i<moveNum;i++){
directionNum=Math.floor(Math.random()*4+1);//产生随机方向数,上下左右四个
//检查是否可以移动
switch(directionNum){
case 1://上
if(currentEmptyY-1>=0){
currentEmptyY--;
operateStack.push(emptyMoveDown);
doExchange=true;
}else{
doExchange=false;
}
break;
case 2://下
if(currentEmptyY+1<difficulty){
currentEmptyY++;
operateStack.push(emptyMoveUp);
doExchange=true;
}else{
doExchange=false;
}
break;
case 3://左
if(currentEmptyX-1>=0){
currentEmptyX--;
operateStack.push(emptyMoveRight);
doExchange=true;
}else{
doExchange=false;
}
break;
case 4://右
if(currentEmptyX+1<difficulty){
currentEmptyX++;
operateStack.push(emptyMoveLeft);
doExchange=true;
}else{
doExchange=false;
}
break;
}
if(doExchange){//执行交换
targetPositionId=currentEmptyX+currentEmptyY*difficulty;
tempPosition=positions[targetPositionId];
positions[targetPositionId]=positions[emptyPositionId];
positions[emptyPositionId]=tempPosition;
emptyPositionId=targetPositionId;
}
}
emptyBlockId=emptyPositionId;//记录空块id
return positions;
}
`
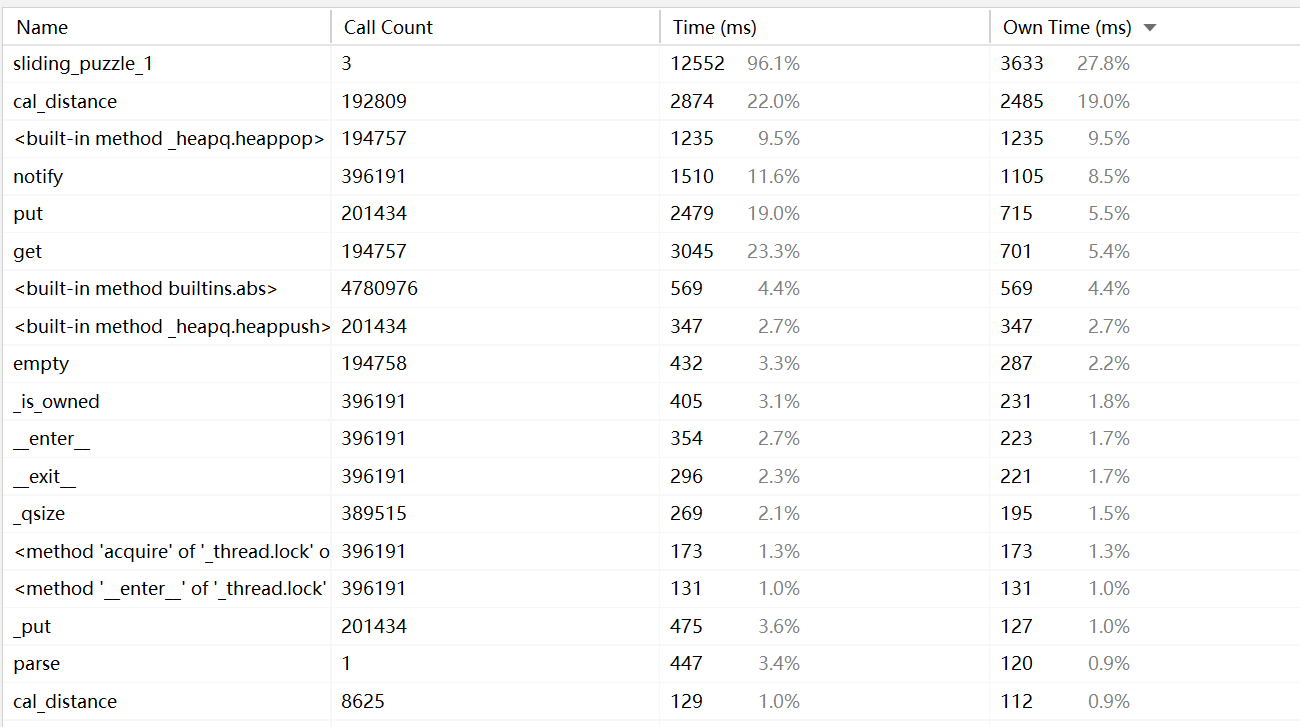
AI性能

游戏部分性能

单元测试:
`
import unittest
from AI import sliding_puzzle_2
class MyTestCase(unittest.TestCase):
def test_something(self):
swap_res = []
# 第二个条件, step步时则替换图片
step = 10
swap = [3, 5]
# board = [[1, 8, 0],
# [6, 5, 4],
# [2, 7, 3]]
board = [[2, 1, 0],
[6, 5, 4],
[8, 7, 3]]
res = sliding_puzzle_2(board, step, swap)
if res[0] != -1:
# print(res)
print(res[0])
print(res[1])
if __name__ == '__main__':
unittest.main()
`
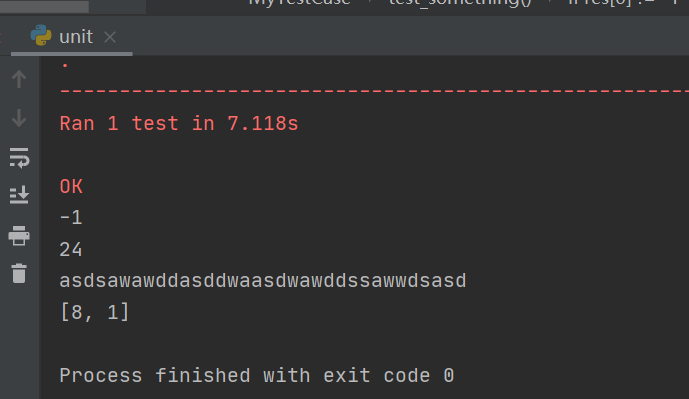
表示一共用了24步完成拼图,其中在第10步的时候交换了第8张跟第1张图片。
(三)遇到的问题:
不知道该怎么用wasd字符输出路线,,,这是困扰我们最大的问题,询问大佬后,大佬说可以采用数组回溯的方法,再用wasd字符表示,经过无数次尝试之后,发现还可以,不愧是大佬。所以有时候遇到问题,自己埋头苦干也许并不是一件好事,询问一下有能力的人,可以节省很多时间与精力。
(四)评价我的队友:
值得学习的地方:佳乐很有耐心,做事比较细致,遇到不好解决的问题,她会很耐心地去查找解决办法,或者去问同学或者去网上找相关资料,遇事不急躁,这一点我必须要向她学习。
需要改进的地方:对代码的解读能力还需要加强。
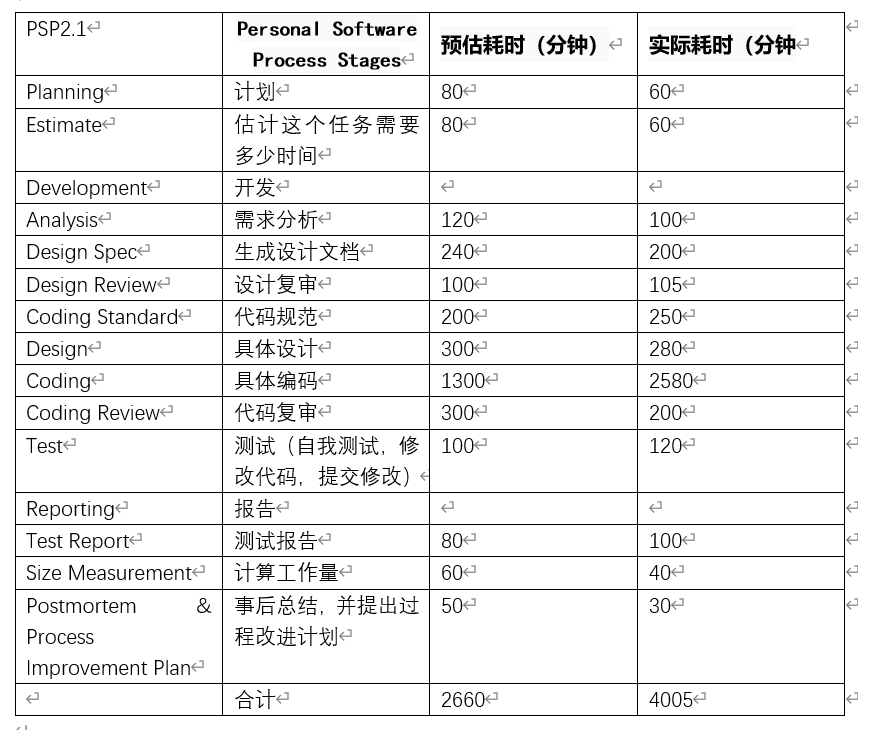
PSP和学习进度条
| 第N周 | 新增代码(行) | 累计代码(行) | 本周学习耗时(小时) | 累计学习耗时(小时) | 重要成长 |
|---|---|---|---|---|---|
| 1 | 111 | 111 | 10 | 10 | 熟悉了用JavaScript创建原型,并且用语言切割图片及处理 |
| 2 | 36 | 147 | 8 | 18 | 用JSON连接原型配置文件,并添加了键盘操作功能,学习到了对键盘事件的监听 |
| 3 | 56 | 203 | 18 | 36 | 实现了游戏中的提示功能 |
| 4 | 74 | 277 | 25 | 61 | 通过了解数组的回溯功能,实现了玩家操作的路线输出 |