生存分析 三大块内容:
1,描述性的
生存率、中位生存期、生存曲线等,常用Kaplan-meier法
2,比较分析
两组的生存曲线是否有差别,log-rank检验(单个因素)
3,cox比例风险回归
类似logistic回归,多个变量对Y的影响,得到一个概率值,只不过加了时间
多花点时间聊聊cox的感受
首先理解一个概念
风险函数(hazard function)h(t)=f(t)/S(t)
f(t)为瞬时死亡率,其实就是时间趋近于零时刻的死亡率,又称死亡概率密度函数,曲线下面积为1.
S(t)为生存率:a, 若无删失,表示为t时刻存活人数/总观察人数
b,若有删失,计算为各个时段下生存概率的乘积( 生存概率:活过该年的人数/年初人数)
象形的理解,瞬时死亡率只受到某时刻,死亡人数的影响,若t时刻死亡10人,瞬时死亡率肯定高于t+1时刻死亡1人
而,生存率,会越来越低。
对于COX风险比例模型,h(t,x)=h0(t)exp(βX)=h0(t)exp(β1x1+β2x2+```+βx)
前半部分为基线风险函数,不需要特定分布,为非参
后半部分相当于对多重线性回归的输出进行了次方变换,保证了 正值和 单调性 (参数模型)
两者相乘即为COX,(半参)
那么聊聊参数估计
对偏似然函数 ,采用极大似然估计
先不管这个所谓偏似然函数,极大似然估计,思想是使得当前样本出现的概率最大。
比如,有三个人X1,X2,X3,分别在t=1,2,3时刻 死去
当t=1时,我们希望模型的似然函数最大,起码有max(1,X1) min(1,X2) min(1,X3)
我们可以构建这样的似然函数:
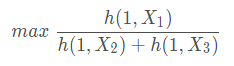
当t=2,

但是t=3时,没有分母可以使用。
所以我们在分母加入了分子本身作为平滑,但是不影响整个分数值得大小趋势。
最后将这三个似然函数连乘:
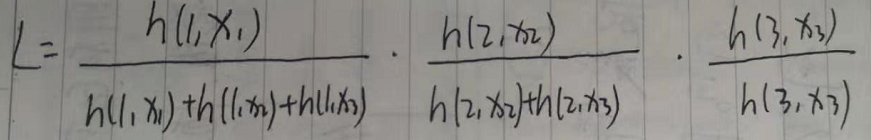
消去h0(t),就可以理解课本上得公式了
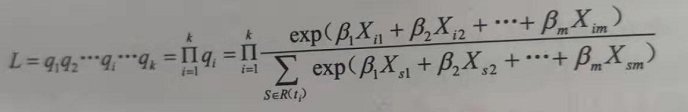
对于PH(比例风险(Proportional hazards)假设,即协变量对生存率的影响不随时间的改变而改变
对协变量检验是否满足PH假设
1,分类变量,图示法:生存曲线是否交叉,log minus log是否交叉(在cox regression中将分类变量放入 层(stata)中,save  )
)
2,连续性变量,Schoenfeld残差法,协变量偏残差(cox--save)与时间秩次(transform--rank case)是否有相关关系,散点图拟合平滑曲线是否有上升下降趋势。
若协变量不满足PH假设,采用时依系数法,即拟合cox函数时,加入一项 x·ln(time)协变量与时间的对数乘积作为交互项,看该项系数是否有统计学差异,若有解释HR应该这样

参考:https://www.cnblogs.com/hapjin/p/6623431.html
https://blog.csdn.net/qq_37523061/article/details/84635614
https://www.mediecogroup.com/method_topic_article_detail/318/?ty=methods
https://www.mediecogroup.com/method_topic_article_detail/320/?ty=methods
https://www.mediecogroup.com/method_topic_article_detail/364/