最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。
示例 2：

输入：s = "cbbd"
输出："bb"
示例 3：

输入：s = "a"
输出："a"
示例 4：

输入：s = "ac"
输出："a"
 

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母（大写和/或小写）组成

解法一：

对于字符串abccba或者abcdcba，满足s[i]==s[len(s)-1-i]时，字符串被称为回文字符串。

这个解法的缺点是运行时间很长。

def longestPalindrome(s):
    length =  len(s)
    max_palindrome = None
    max_length = 0
    for i in range(length):
        if (length-i)<=max_length:
            break
        for j in range(length-i):
            length_palindrome = (length - i) - j
            if length_palindrome<=max_length:
                break
            for k in range(length_palindrome):
                if s[i+k]==s[(length-1-j)-k]:
                    if (((length-1-j)-k)-(i+k)) in [0,1]:
                        if length_palindrome > max_length:
                            max_palindrome = s[i:(i+length_palindrome)]
                            max_length = length_palindrome
                        break
                else:
                    break
    return max_palindrome

解法二：

动态规划
思路与算法

对于一个子串而言，如果它是回文串，并且长度大于 22，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串 \textrm{``ababa''}“ababa”，如果我们已经知道 \textrm{``bab''}“bab” 是回文串，那么 \textrm{``ababa''}“ababa” 一定是回文串，这是因为它的首尾两个字母都是 \textrm{``a''}“a”。

根据这样的思路，我们就可以用动态规划的方法解决本题。我们用 P(i,j)P(i,j) 表示字符串 ss 的第 ii 到 jj 个字母组成的串（下文表示成 s[i:j]s[i:j]）是否为回文串：

这里的「其它情况」包含两种可能性：

那么我们就可以写出动态规划的状态转移方程：

也就是说，只有 s[i+1:j-1]s[i+1:j−1] 是回文串，并且 ss 的第 ii 和 jj 个字母相同时，s[i:j]s[i:j] 才会是回文串。

上文的所有讨论是建立在子串长度大于 22 的前提之上的，我们还需要考虑动态规划中的边界条件，即子串的长度为 11 或 22。对于长度为 11 的子串，它显然是个回文串；对于长度为 22 的子串，只要它的两个字母相同，它就是一个回文串。因此我们就可以写出动态规划的边界条件：

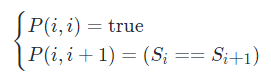
根据这个思路，我们就可以完成动态规划了，最终的答案即为所有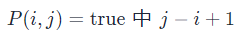（即子串长度）的最大值。注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

​

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        if n < 2:
            return s
        
        max_len = 1
        begin = 0
        # dp[i][j] 表示 s[i..j] 是否是回文串
        dp = [[False] * n for _ in range(n)]
        for i in range(n):
            dp[i][i] = True
        
        # 递推开始
        # 先枚举子串长度
        for L in range(2, n + 1):
            # 枚举左边界，左边界的上限设置可以宽松一些
            for i in range(n):
                # 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                j = L + i - 1
                # 如果右边界越界，就可以退出当前循环
                if j >= n:
                    break
                    
                if s[i] != s[j]:
                    dp[i][j] = False 
                else:
                    if j - i < 3:
                        dp[i][j] = True
                    else:
                        dp[i][j] = dp[i + 1][j - 1]
                
                # 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if dp[i][j] and j - i + 1 > max_len:
                    max_len = j - i + 1
                    begin = i
        return s[begin:begin + max_len]

解法原文：

https://leetcode-cn.com/problems/longest-palindromic-substring/solution/zui-chang-hui-wen-zi-chuan-by-leetcode-solution/