zoukankan html css js c++ java

算法与数据结构

算法引入

import time

start_time = time.time()
for a in range(0, 1001):
    for b in range(0, 1001):
        for c in range(0, 1001):
            if a+b+c == 1000 and a**2 + b**2 == c**2:
                print("a, b, c:%d, %d, %d" % (a, b, c))

end_time = time.time()
print("times:%d" % (end_time -start_time))
print("finished")

执行结果

a, b, c:0, 500, 500
a, b, c:200, 375, 425
a, b, c:375, 200, 425
a, b, c:500, 0, 500
times:286
finished

另一种算法

import time

start_time = time.time()
for a in range(0, 1001):
    for b in range(0, 1001):
        c = 1000 - a - b
        if a**2 + b**2 == c**2:
            print("a, b, c:%d, %d, %d" % (a, b, c))

end_time = time.time()
print("times:%d" % (end_time -start_time))
print("finished")

执行结果

a, b, c:0, 500, 500
a, b, c:200, 375, 425
a, b, c:375, 200, 425
a, b, c:500, 0, 500
times:1
finished

算法的概念

算法是独立存在的一种解决问题的方法和思想

算法的特性:

输入
输出
有穷性
确定性
可行性

算法效率衡量

时间复杂度
基本运算数量个数

T1 = O(n^3)
T2 = O(n^2)
只考虑与n相关的数量级,忽略常量系数(最后的循环中有2个还是10个操作)

最优时间复杂度
最坏时间复杂度
平均时间复杂度

一般时间复杂度指最坏时间复杂度

时间复杂度计算规则:

常见时间复杂度

Python内置类型性能分析

from timeit import Timer

def test1():
    li = []
    for i in range(10000):
        # li += [i]  不完全等于以下语句, 有优化
        li = li + [i]

def test2():
    li = []
    for i in range(10000):
        li.append(i)

def test3():
    li = [i for i in range(10000)]

def test4():
    li = list(range(10000))

def test5():
    li = []
    for i in range(10000):
        li.extend([i])

def test6():
    li = []
    for i in range(10000):
        li.insert(0, i)

timer1 = Timer("test1()", "from __main__ import test1")
print("+:", timer1.timeit(number=1000))

timer2 = Timer("test2()", "from __main__ import test2")
print("append:", timer2.timeit(number=1000))

timer3 = Timer("test3()", "from __main__ import test3")
print("构造器:", timer3.timeit(number=1000))

timer4 = Timer("test4()", "from __main__ import test4")
print("类型转换:", timer4.timeit(number=1000))

timer5 = Timer("test5()", "from __main__ import test5")
print("extend:", timer5.timeit(number=1000))

timer6 = Timer("test6()", "from __main__ import test6")
print("insert:", timer6.timeit(number=1000))

执行结果

+: 1.9438251314738715
append: 2.0546681004856353
构造器: 0.9054245635968021
类型转换: 0.5199876041759088
extend: 2.7770162085994707
insert: 42.24719570966755

数据结构

静态的描述了数据元素之间的关系

程序 = 数据结构+算法

抽象数据类型 ADT
数据组装方式 + 所支持的操作

顺序表

用连续单元存储数据(地址连续)

变量名指向起始地址

索引实际是从起始位置的偏移量

一体存储元素内置
分离存储元素外置
动态顺序表(可以数据扩充)

顺序表的操作

添加元素末尾添加 O(1) 中间插入O(n) 插入非保序O(1)
删除元素末尾删除 O(1) 中间删除O(n)

Python的list的基本实现

链表

一个节点分为两部分,数据区和链接区, 链接区指向下一个节点
单项链表

a, b = b, a的本质
python中变量是一块单独的空间, 其中保存的是所代表对象的地址

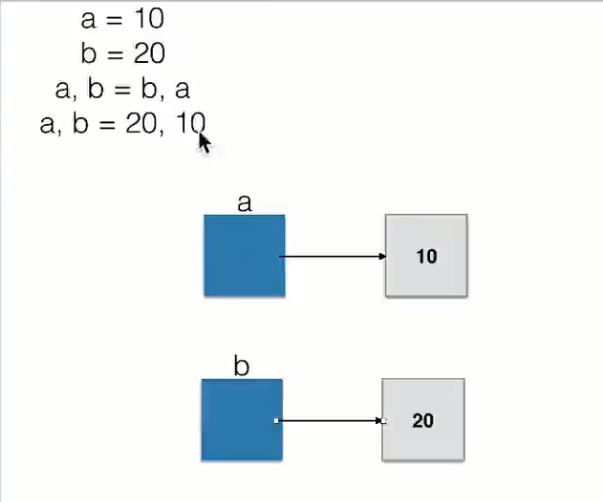
单项链表的实现

"""单项链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class SingleLinkList(object):
    def __init__(self, node=None):
        self.__head = node

    def add(self, item):
        node = Node(item)
        if self.__head:
            self.__head, node.next = node, self.__head
        else:
            self.__head = node

    def append(self, item):
        node = Node(item)
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        else:
            self.__head = node
        
    def travel(self):
        if self.__head:
            cur = self.__head
            while cur is not None:
                print(cur.elem)
                cur = cur.next

    def remove(self, item):
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                if cur.next.elem == item:
                    cur.next = cur.next.next
                    break
                cur = cur.next
            else:
                print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item):
        i = 0
        cur = self.__head
        if pos == 0:
            self.add(item)
        elif pos + 1 > self.length:
            raise ValueError
        else:
            while cur.next is not None:
                i += 1
                if i == pos:
                    new_node = Node(item)
                    cur.next, new_node.next = new_node, cur.next
                    break
                elif i > pos:
                    raise ValueError
                cur = cur.next

    def search(self, item):
        if self.__head:
            cur = self.__head
            while cur is not None:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next

    @property
    def length(self):
        count = 0
        if self.__head:
            cur = self.__head
            while cur is not None:
                count += 1
                cur = cur.next
        return count

    def is_empty(self):
        return self.__head is None

循环链表
循环链表的实现


"""循环链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class CircleLinkList(object):
    def __init__(self, node=None):
        if node is None:
            self._head = None
        else:
            self._head = node.next = node

    def add(self, item):
        node = Node(item)
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur
            node.next, self._head = self._head, node
            last.next = self._head
        else:
            self._head = node.next = node

    def append(self, item):
        node = Node(item)
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur
            last.next, node.next = node, self._head
        else:
            self._head = node.next = node
        
    def travel(self):
        if self._head:
            cur = self._head
            while cur.next != self._head:
                print(cur.elem, end=" ")
                cur = cur.next
            print(cur.elem)

    def remove(self, item):   # 单节点remove
        if self._head:
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            last = cur

            cur = self._head
            if cur.elem == item:
                self._head = last.next = cur.next
            else:
                while cur.next != self._head:
                    if cur.next.elem == item:
                        cur.next = cur.next.next
                        break
                    cur = cur.next 
                else:
                    print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item): 
        length = self.length
        if pos == 0:
            self.add(item)
        elif pos == length:
            self.append(item)
        elif pos > length:
            raise ValueError
        else:
            i = 0
            cur = self._head
            while cur.next != self._head :
                i += 1
                if i == pos:
                    node = Node(item)
                    cur.next, node.next = node, cur.next
                    break
                cur = cur.next

    def search(self, item):
        if self._head:
            cur = self._head
            while cur.next != self._head:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next
            else:
                if cur.elem == item:
                    print(cur.elem)

    @property
    def length(self):
        count = 0
        if self._head:
            cur = self._head
            while cur.next != self._head:
                count += 1
                cur = cur.next
            count += 1
        return count

    def is_empty(self):
        return self._head is None

if __name__ == '__main__':
    s = CircleLinkList()
    s.append(0)
    s.append(1)
    s.append(2)
    s.append(3)
    s.remove(0)
    s.insert(3, 4)
    s.search(1)
    s.travel()

双向链表
双向链表的实现

"""双项链表的实现"""
class Node(object):
    def __init__(self, elem):
        self.pre = None
        self.elem = elem
        self.next = None
    def __repr__(self):
        return "<Node: {}>".format(self.elem)

class DoubleLinkList(object):
    def __init__(self, node=None):
        self.__head = node

    def add(self, item):
        node = Node(item)
        if self.__head:
            self.__head, self.__head.pre, node.next = node, node, self.__head
        else:
            self.__head = node

    def append(self, item):
        node = Node(item)
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            cur.next, node.pre = node, cur
        else:
            self.__head = node
        
    def travel(self):
        if self.__head:
            cur = self.__head
            while cur is not None:
                print(cur.elem, end=" ")
                cur = cur.next

    def remove(self, item):
        if self.__head:
            cur = self.__head
            while cur.next is not None:
                if cur.next.elem == item:
                    cur.next, cur.next.next.pre = cur.next.next, cur
                    break
                cur = cur.next
            else:
                print("Not Exist")
        else:
            print("Not Exist")

    def insert(self, pos, item):
        i = 0
        cur = self.__head
        if pos == 0:
            self.add(item)
        elif pos + 1 > self.length:
            raise ValueError
        else:
            while cur.next is not None:
                i += 1
                if i == pos:
                    new_node = Node(item)
                    cur.next, new_node.next, new_node.pre = new_node, cur.next, cur
                    break
                elif i > pos:
                    raise ValueError
                cur = cur.next

    def search(self, item):
        if self.__head:
            cur = self.__head
            while cur is not None:
                if cur.elem == item:
                    print(cur.elem)
                    break
                cur = cur.next

    @property
    def length(self):
        count = 0
        if self.__head:
            cur = self.__head
            while cur is not None:
                count += 1
                cur = cur.next
        return count

    def is_empty(self):
        return self.__head is None

顺序表和链表统称线性表

栈

堆和栈一样吗?
栈(stack)一般编译器自动分配释放
堆(heap)一般由程序员分配释放,或程序结束后OS释放
LIFO 后进先出

栈的实现

class Stack(object):
    def __init__(self):
        self.__list = []
    def push(self, item):
        self.__list.append(item)

    def pop(self):
        return self.__list.pop()

    def peek(self):
        if self.__list:
            return self.__list[-1]
        else:
            return None

    def is_empoty(self):
        return self.__list == []

    def size(self):
        return len(self.__list)

if __name__ == '__main__':
    s = Stack()
    a = "({[({{abc}})][{1}]})2([]){({[]})}[]"
    m = {')':'(',']':'[','}':'{'}
    for i in a:
        if i in '([{':
            s.push(i)
        elif i in m:
            if m[i] != s.pop():
                print("fail")
                break
    else:
        print("ok")

队列

FIFO 先进先出

队列与双端队列的实现

class Queue(object):
    def __init__(self):
        self.__list = []

    def enqueue(self, item):
        self.__list.append(item)

    def dequeue(self):
        return self.__list.pop(0)

    def is_empty():
        return self.__list == []

    def size():
        return len(self.__list)

if __name__ == '__main__':
    q = Queue()
    q.enqueue(1)


class Dqueue(object):
    def __init__(self):
        self.__list = []

    def add_front(self, item):
        self.__list.insert(0, item)

    def add_rear(item):
        self.__list.append(item)

    def pop_front(self):
        return self.__list.pop(0)

    def pop_rear(self):
        return self.__list.pop()

    def is_empty():
        return self.__list == []

    def size():
        return len(self.__list)

if __name__ == '__main__':
    d = Dqueue()

排序与搜索

排序算法的稳定性: [2, 1, 1 , 3], 如果其中有相同元素, 算法不应破坏原有顺序

排序算法

l = [4, 2, 1, 8, 5, 2, 3, 0, 9, 8, 10, 4, 3, 2]


def buddle_sort(l):
    length = len(l)
    for i in range(length-1):
        for j in range(length-i-1):
            if l[j] > l[j+1]:
                l[j], l[j+1] = l[j+1], l[j]


def select_sort(l):
    length = len(l)
    for j in range(length):
        max_index = 0
        for i in range(length-j):
            if l[i] > l[max_index]:
                max_index = i
        l[max_index], l[length-j-1] = l[length-j-1], l[max_index]


def quick_sort(l):
    length = len(l)
    if length < 2:
        return l

    mid = length // 2
    low_part = [i for i in l[1:] if i < l[mid]]
    eq_part = [i for i in l[1:] if i == l[mid]]
    high_part = [i for i in l[1:] if i > l[mid]]
    return quick_sort(low_part) + eq_part + quick_sort(high_part)


def quick_sort2(l, start, end):
    low, high = start, end
    if low >= high:
        return
    mid = l[low]
    while low < high:
        while low < high and l[high] > mid:
            high -= 1
        l[low] = l[high]
        while low< high and l[low] <= mid:
            low += 1
        l[high] = l[low]
    l[low] = mid

    quick_sort2(l, start, low-1)
    quick_sort2(l, low+1, end)


def insert_sort(l):
    for i in range(1, len(l)):
        for j in range(i, 0, -1):
            if l[j] < l[j-1]:
                l[j-1], l[j] = l[j], l[j-1]  
    # 感觉类似冒泡, 冒泡每次从底层开始冒, 插入每次从有序的后一个往前

# 希尔排序
def shell_sort(l):
    n = len(l)
    gap = n//2
    while gap > 0:
        for i in range(gap, n):
            j = i
            # 插入排序
            while j>=gap and l[j-gap] > l[j]:
                l[j-gap], l[j] = l[j], l[j-gap]
                j -= gap
        gap =gap//2
     
# 归并排序
def merge(left, right):
    '''合并操作'''
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]  # 加上剩余的元素
    result += right[r:] # 加上剩余的元素
    return result
    
def merge_sort(l):
    if len(l) <=1:
        return l
    num = len(l) // 2
    left = merge_sort(l[:num])
    right = merge_sort(l[num:])
    return merge(left, right)


if __name__ == '__main__':
    # buddle_sort(l)
    # print(l)
    # select_sort(l)
    # print(l)
    # quick_sort(l)
    # print(l)
    # quick_sort2(l, 0, len(l)-1)
    insert_sort(l)
    print(l)

冒泡排序: 依次比较相邻两个位置,将大的交换到最后, 重复剩余部分
选择排序: 先找到最大(最小)值的索引, 将最大数(最小输)和最后(最前)一个交换, 重复剩余部分
快速排序: 选一个基准数,将小于基准数和大于基准数的分为两部分,递归左右两部分直到长度小于2
插入排序: 从第二位依次向前比较交换,保持前半部分有序
希尔排序: 按不同间隔(间隔从n/2到1)进行插入排序
归并排序: 递归将两个有序序列合并成一个新的有序序列

冒泡,插入,归并是稳定的

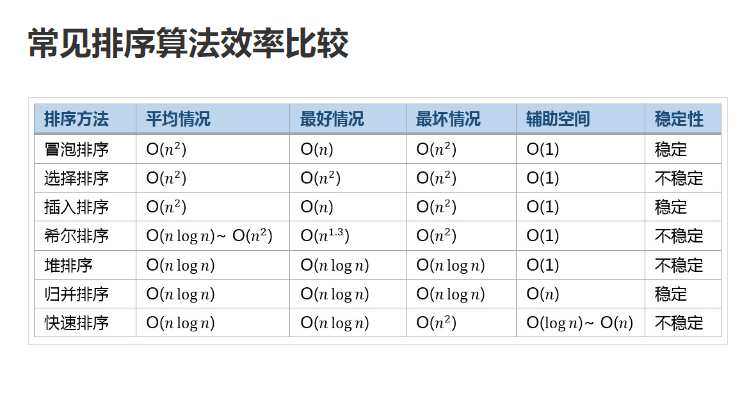
树和二叉树

完全二叉树: 除了最下层,每一层都满了
满二叉树: 每一层都满了
平衡二叉树: 任意两个节点的高度差不大于1
排序二叉树:

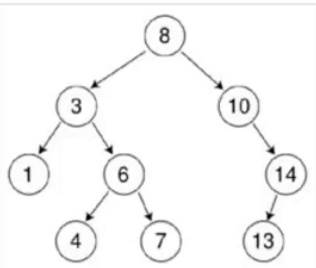
链式存储

常见应用场景

xml/html解析
路由协议
mysql数据库索引
文件系统结构

二叉树

在二叉树的第i层上至多有2^(i-1)个结点
深度为k的二叉树至多有2^k-1个结点
对于任意一颗二叉树, 如果其叶结点数为N, 则度数为2的节点总数为N+1
具有n个节点的完全二叉树的深度必为log2(n+1)
对于完全二叉树, i节点的左孩子变化为2i, 右孩子为2i+1

二叉树的节点表示和树的创建

节点

class Node(object):
    def __init__(self, item):
        self.elem = item
        self.lchild = lchild
        self.rchild = rchild

树

class Tree(object):
    def __init__(self, root=None):
        self.root = root
        
    def add(self, item):
        node = Node(item)
        if self.root is None
            self.root = node
            return
        else:
        queue = [self.root]
        while queue:
            cur_node = queue.pop(0)
            if cur_node.lchild is None:
                cur_node.lchild = node
                return
            else:
                queue.append(cur_node.lchild)
            if cur_node.rchild is None:
                cur_node.rchild = node
                return
            else:
                queue.append(cur_node.rchild)
                
    # 广度优先遍历
    def breadth_travel(self):
        if self.root is None:
            return
        queue = [self.root]
        while queue:
            cur_node = queuq.pop(0)
            print(cur_node.elem)
            if cur_node.lchild is not None:
                quequ.append(cur_node.lchild)
            if cur_node.rchild is not None:
                queue.append(rchild)
                
    # 先序遍历
    def preorder(self, node):
        if node is None:
            return
        print(node.elem)
        self.preorder(node.lchild)
        self.preorder(node.rchild)
        
    # 中序遍历
    def inorder(self, node):
        if node is None:
            return
        self.inorder(node.lchild)
        print(node.elem)
        self.inorder(node.rchild)
        
    # 后序遍历
    def postorder(self, node):
        if node is None:
            return
        self.postorder(node.lchild)
        self.postorder(node.rchild)
        print(self.elem)

根据先序遍历+中序遍历或后序+中序推导出一颗树

先从先序/后序中找出root节点
在中序中找到root节点分成两半
先序中安装中序中的两半分开
左右子树分别重复前三步操作

查看全文

相关阅读:
myeclipse-9.0安装svn客户端插件
 jquery中lhgdialog插件（一）
Jquery之ShowLoading遮罩组件
 git 命令
 org.apache.ibatis.builder.IncompleteElementException: Could not find parameter map
在线压缩图片网址
 如何在知网下载外文文献
 Linux 常见命令
 在VIM 里面编辑和保存
 vi a.sh ABCD

原文地址：https://www.cnblogs.com/superhin/p/12294891.html

最新文章
150.关系
 149.集合论
 148.离散数学_谓词逻辑
 克隆模式
 单例模式
 抽象工厂
 工厂方法
 简单工厂，静态工厂
 设计模式原则概述
 构造函数笔试题