[题解]luogu_P3304直径（直径必经边

这题做法好多好多啊

首先我们发现直径的重合部分一定是类似于

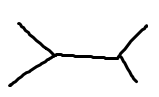这样的

然后考虑产生多条直径的条件，一定是某点走到底和它走到直径的一端长度相同

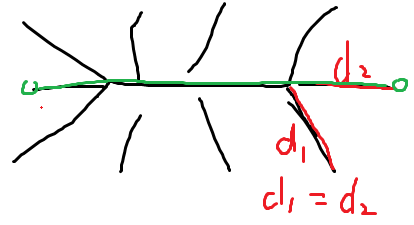
这里的每条线其实可以看做每个点子树最深的地方了，那么我们处理出直径上每个点最深能到达的地方，扫一遍，找到两个端点，这两个端点之间就是必经边了

dis数组用的比较乱，但是是对的

#include<bits/stdc++.h>
using namespace std;
const int maxn=200009;
int n;
struct node{
    int v,nxt,w;
}e[maxn<<1];
int head[maxn],cnt;
inline void add(int u,int v,int w){
    e[++cnt].v=v;e[cnt].w=w;e[cnt].nxt=head[u];head[u]=cnt;
}
int fa[maxn],far;
long long dis[maxn];
bool dia[maxn];
void dfs(int x,int f){
    fa[x]=f;
    if(dis[x]>dis[far])far=x;
    for(int i=head[x];i;i=e[i].nxt){
        int y=e[i].v;
        if(y==f||dia[y])continue;
        dis[y]=dis[x]+e[i].w;
        dfs(y,x);
    }
}
int main(){
    scanf("%d",&n);
    for(int i=1,u,v,w;i<n;i++){
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);add(v,u,w);
    }
    dfs(1,0);int l=far;
    dis[far]=0;dfs(far,0);
    printf("%lld
",dis[far]);
    int r=far;
    for(int i=r;i;i=fa[i])dia[i]=1;
    bool flg=0;
    int ll=l,rr=r;
    for(int i=fa[rr];i!=ll;i=fa[i]){
        int ld=dis[i],rd=dis[rr]-dis[i];//到左右端点距离 
        dis[i]=0;far=i;
        dfs(i,fa[i]);
        if(dis[far]==rd)r=i;//子树深度和右端点距离相同，有其他直径 
        if(dis[far]==ld&&!flg)flg=1,l=i;//第一次最优 
    }
    int ans=1;
    for(int i=fa[r];i!=l;i=fa[i])ans++;
    printf("%d
",ans);
}