AVL Tree
An AVL tree is a kind of balanced binary search tree. Named after their inventors, Adelson-Velskii and Landis, they were the first dynamically balanced trees to be proposed. Like red-black trees, they are not perfectly balanced, but pairs of sub-trees differ in height by at most 1, maintaining an O(logn) search time. Addition and deletion operations also take O(logn) time.
Definition of an AVL tree
An AVL tree is a binary search tree which has the following properties:
1. The sub-trees of every node differ in height by at most one.
2. Every sub-tree is an AVL tree.
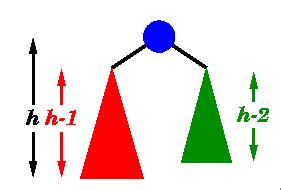
Balance requirement for an AVL tree: the left and right sub-trees differ by at most 1 in height.An AVL tree of n nodes can have different height.
For example, n = 7:
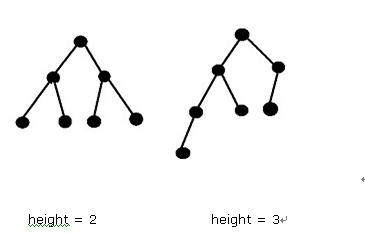
So the maximal height of the AVL Tree with 7 nodes is 3.
Given n,the number of vertices, you are to calculate the maximal hight of the AVL tree with n nodes.
Definition of an AVL tree
An AVL tree is a binary search tree which has the following properties:
1. The sub-trees of every node differ in height by at most one.
2. Every sub-tree is an AVL tree.

Balance requirement for an AVL tree: the left and right sub-trees differ by at most 1 in height.An AVL tree of n nodes can have different height.
For example, n = 7:

So the maximal height of the AVL Tree with 7 nodes is 3.
Given n,the number of vertices, you are to calculate the maximal hight of the AVL tree with n nodes.
Input
Input file contains multiple test cases. Each line of the input is an integer n(0<n<=10^9).
A line with a zero ends the input.
Output
An integer each line representing the maximal height of the AVL tree with n nodes.Sample Input
1 2 0
Sample Output
0 1
解题思路:
本题给出一个整数,要求输出其能建立的最高的平衡二叉树的高度。
关于平衡二叉树最小节点最大高度有一个公式,设height[i]为高度为i的平衡二叉树的最小结点数,则height[i] = height[i - 1] + height[i - 2] + 1;
因为高度为0时平衡二叉树:
#
高度为1时平衡二叉树:
0 # 或 #
/
1 # #
高度为2时平衡二叉树:
0 # 或 #
/ /
1 # # # #
/
2 # #
高度为i时平衡二叉树:
# 或 #
/ /
i - 2 i - 1 i - 1 i - 2
所以只需要将10^9内的数据记录后让输入的数据与之比较就可得到答案。(高度不会超过46)
1 #include <cstdio> 2 using namespace std; 3 const int maxn = 50; 4 int height[maxn]; 5 int main(){ 6 height[0] = 1; 7 height[1] = 2; 8 for(int i = 2; i < maxn; i++){ //记录1 - 50层最小需要多少节点 9 height[i] = height[i - 1] + height[i - 2] + 1; 10 } 11 int n; 12 while(scanf("%d", &n) != EOF){ //输入数据 13 if(n == 0) //如果为0结束程序 14 break; 15 int ans = -1; 16 for(int i = 0; i < maxn; i++){ //从第0层开始比较 17 if(n >= height[i]) //只要输入的数据大于等于该点的最小需求答案高度加一 18 ans++; 19 else 20 break; //否则结束循环 21 } 22 printf("%d ", ans); //输出答案 23 } 24 return 0; 25 }