zoukankan html css js c++ java

PTA (Advanced Level) 1066 Root of AVL Tree

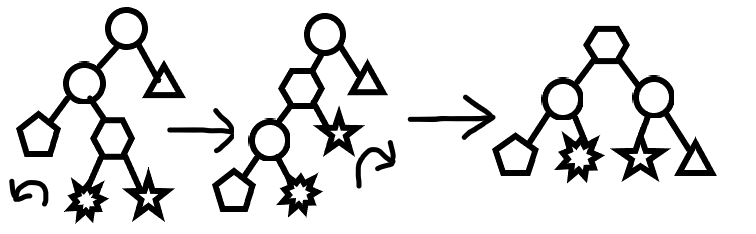
Root of AVL Tree

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

AVL树作用：
　　对于正常二叉搜索树建立过程，以第一个结点为根结点，若输入的结点权值大于第一个结点则插入右子树，小于第一个结点则插入左子树。若遇到出入数据为有序的情况，普通二叉搜索树就会建立一个长链式的树，其查询复杂度就会达到O(n)，如以{1， 2， 3， 4 ，5 ，6， 7， 8， 9， 10}建立的二叉搜索树：

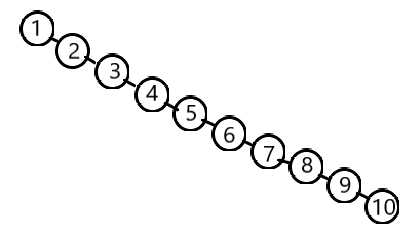
若要保持查询复杂度为O(logn)则需要建立AVL树，只需在插入过程中通过左旋右旋操作保证叶子结点的最大高度差不超过1，以{1， 2， 3， 4 ，5 ，6， 7， 8， 9， 10}建立AVL树：

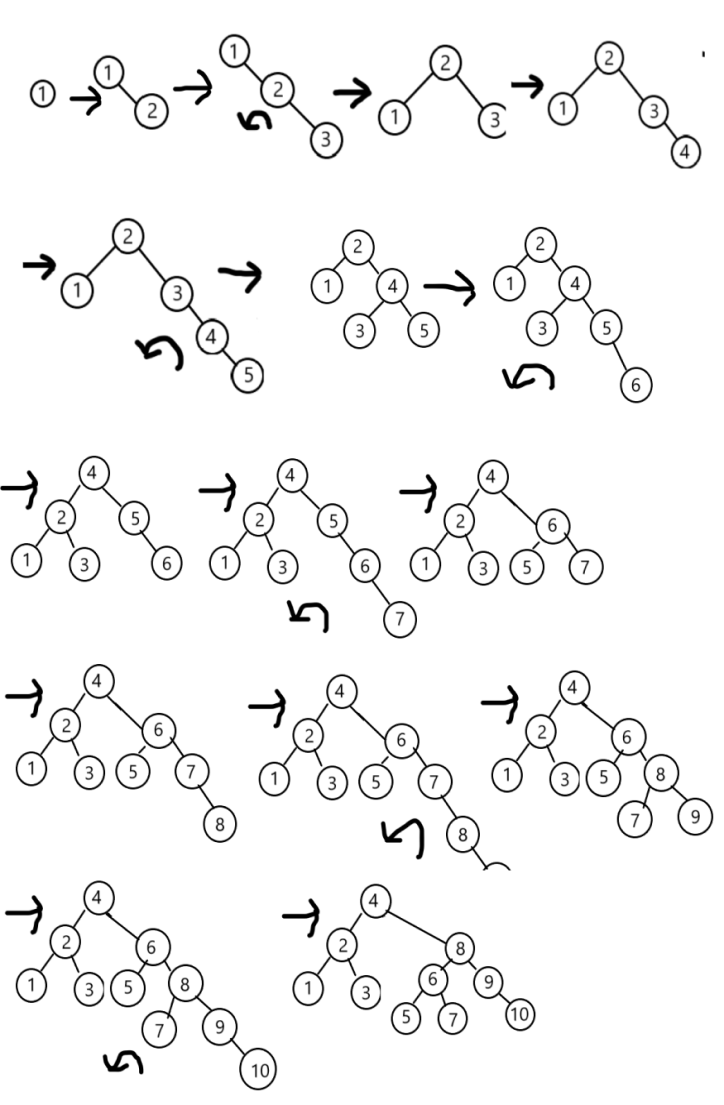
解题思路：
　　AVL树模板题要求按输入建立AVL树即在二叉搜索树叶子结点最大高度差大于等于二的时候进行左旋或右旋进行结构优化使结点深度保持在O(logn)的级别,输出AVL树根结点。

  1 #include <bits/stdc++.h>
  2 using namespace std;
  3 typedef int dataType;
  4 vector<dataType> data;
  5 struct node{
  6     dataType data;
  7     int height; //AVL树结点比起普通二叉搜索树需要记录height
  8     node *leftChild;
  9     node * rightChild;
 10     node(){
 11         height = 1;
 12         leftChild = NULL;
 13         rightChild = NULL;
 14     }
 15 };
 16 int getHeight(node *root){  //获取高度
 17     if(root == NULL)  
 18         return 0;
 19     else
 20         return root->height;
 21 }
 22 int getBalanceFactor(node *root){   //获取树的叶子结点高度差左高为正右高为负
 23     return getHeight(root->leftChild) - getHeight(root->rightChild);
 24 }
 25 int updateHeight(node *root){   //更新高度
 26     root->height = max(getHeight(root->leftChild),getHeight(root->rightChild)) + 1;
 27 }
 28 void leftRotation(node *&root){ //左旋
 29     node *temp = root->rightChild;      //root指向先前根结点temp指向右子树根结点
 30     root->rightChild = temp->leftChild; //temp指向根结点的右子树，所以其所有结点都大于根结点
 31     //由于在左旋中需要使temp成为新的根结点，所以将root右子树指向temp左子树，再让temp左子树指向root
 32     temp->leftChild = root;
 33     //更新root与temp的树高
 34     updateHeight(root);
 35     updateHeight(temp);
 36     root = temp;    //temp成为新的根结点
 37 }
 38 void rightRotation(node *&root){    //右旋思路同左旋
 39     node *temp = root->leftChild;
 40     root->leftChild = temp->rightChild;
 41     temp->rightChild = root;
 42     updateHeight(root);
 43     updateHeight(temp);
 44     root = temp;
 45 }
 46 void insertAVLTree(node *&root, int x){ //插入结点
 47     if(root == NULL){   //找到插入位置
 48         root = new node();
 49         root->data = x;
 50         return;
 51     }
 52     if(root->data == x){    //结点已存在
 53         return;
 54     }else if(root->data > x){   //要插入的数据比根结点权值小
 55         insertAVLTree(root->leftChild, x);  //插入左子树
 56         updateHeight(root);
 57         if(getBalanceFactor(root) == 2){　　//插入左子树时只可能出现左子树比右子树高的情况
 58             if(getBalanceFactor(root->leftChild) == 1){　　//若左子树的左子树较高直接右旋
 59                 rightRotation(root);
 60             }else if(getBalanceFactor(root->leftChild) == -1){　　//若左子树中右子树较高则将其通过右旋转化为左子树高的情况　　种情况详见下图
 61                 leftRotation(root->leftChild);
 62                 rightRotation(root);
 63             }
 64         }
 65     }else if(root->data < x){   //要插入的数据比根结点权值大
 66         insertAVLTree(root->rightChild, x); //插入右子树
 67         updateHeight(root);
 68         if(getBalanceFactor(root) == -2){
 69             if(getBalanceFactor(root->rightChild) == -1){
 70                 leftRotation(root);
 71             }else if(getBalanceFactor(root->rightChild) == 1){
 72                 rightRotation(root->rightChild);
 73                 leftRotation(root);
 74             }
 75         }
 76     }
 77 }
 78 node *createAVLTree(){
 79     node *root = NULL;
 80     for(vector<dataType>::iterator it = data.begin(); it != data.end(); it++){
 81         insertAVLTree(root, *it);
 82     }
 83     return root;
 84 }
 85 /*void preorder(node *root){
 86     if(root == NULL)
 87         return;
 88     cout << root -> data << " ";
 89     preorder(root -> leftChild);
 90     preorder(root -> rightChild);
 91 }*/
 92 int main()
 93 {
 94     int n;
 95     while(scanf("%d", &n) != EOF){
 96         data.clear();
 97         for(int i = 0; i < n; i++){
 98             dataType temp;
 99             scanf("%d", &temp);
100             data.push_back(temp);
101         }
102         node *root = createAVLTree();
103         //preorder(root);
104         //cout << endl;
105         printf("%d
", root->data);
106     }
107     return 0;
108 }

左子树的左子树较高

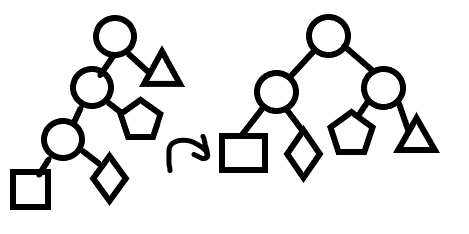
左子树的右子树较高

查看全文

相关阅读:
Maven常用命令：
正向代理、反向代理、透明代理
 linux命令ps aux|grep xxx详解
 Java中Comparable和Comparator区别小结
 Java Queue之PriorityQueue
java读写分离的实现
 CSS颜色名称和颜色值
 使用Access-Control-Allow-Origin解决跨域
 Tomcat 下启用 https:// 访问
 使用Jedis操作redis

原文地址：https://www.cnblogs.com/suvvm/p/9893303.html