tarjan缩点

可达性-牛客（tarjan缩点）

题意： 给出一个 0 ≤ N ≤ 10⁵ 点数、0 ≤ M ≤ 10⁵ 边数的有向图，输出一个尽可能小的点集，使得从这些点出发能够到达任意一点，如果有多个这样的集合，输出这些集合升序排序后字典序最小的。

解：缩点，如果只有一个点直接输出1，整张图连通。

缩点过程，维护两个数组fa[]点集字典序最小的店和num[]保存新点的点集,缩点所代表的点有哪些

直接tarjan算法求即可。

样例模拟：

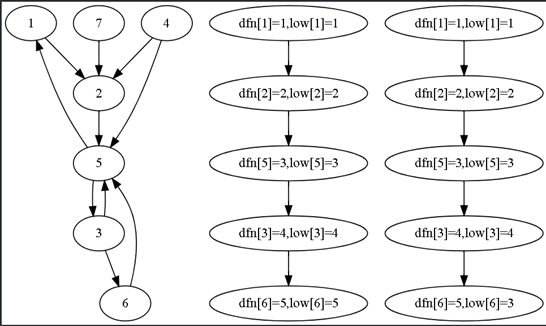
回溯到3，回溯到5

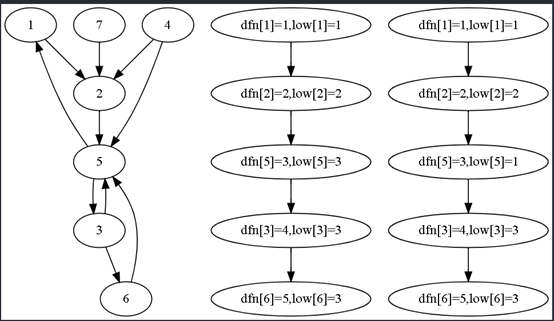
回溯到5之后更改low【5】=1；

回溯到2,更改low2=1；回溯到1，出栈；

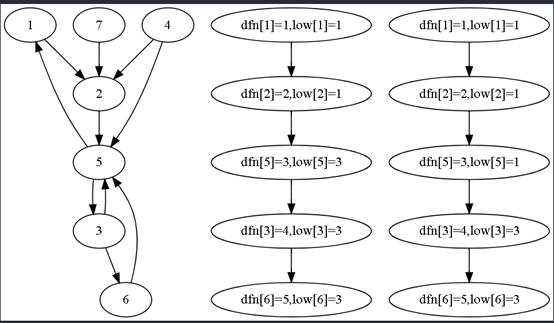
代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
const int mod=142857;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair<int,int> pii;
const int N=5e5+10;
 
struct node
{
    int v,next;
}G[maxn];
int head[maxn],cnt;
 
void add(int x,int y)
{
    G[++cnt]=node{y,head[x]};
    head[x]=cnt;
}
 
int dfn[maxn],low[maxn],tot;
stack<int> st;
int vis[maxn];
int fa[maxn],num[maxn],ncnt;
 
void tarjan(int u)
{
    dfn[u]=low[u]=++tot;
    st.push(u);
    vis[u]=1;
    for(int i=head[u]; i!=-1; i=G[i].next)
    {
        int v=G[i].v;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(vis[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        ncnt++;
        int t;
        do{
            t=st.top();
            st.pop();
            num[t]=ncnt;
            fa[ncnt]=min(t,fa[cnt]);//初始置无限大;
            vis[t]=0;
        }while(t!=u);
    }
}
int n,m;
int ans[maxn],x;
int in[maxn];
int main()
{
    cin>>n>>m;
    memset(fa,inf,sizeof(fa));
    memset(head,-1,sizeof(head));
    for(int i=1; i<=m; i++)
    {
        int u,v;
        cin>>u>>v;
        add(u,v);
    }
    for(int i=1; i<=n; i++)
    {
        if(!dfn[i])
         tarjan(i);
    }
    if(ncnt==1)
     cout<<1<<endl;
    else
    {
        for(int i=1; i<=n; i++)
        {
            for(int j=head[i]; j!=-1; j=G[j].next)
            {
                int u=num[i];
                int v=num[G[j].v];
                if(u!=v)
                 in[v]++;
            }
        }
        for(int i=1; i<=ncnt; i++)
        {
            if(!in[i])
             ans[x++]=fa[i];
        }
        sort(ans,ans+x);
        cout<<x<<endl;
        for(int i=0; i<x; i++) cout<<ans[i]<<" ";
        cout<<"
";
    }
    system("pause");
 
}