Codeforces Round #587 (Div. 2) C

http://codeforces.com/contest/1230/problem/C

C. Anadi and Domino

Anadi has a set of dominoes. Every domino has two parts, and each part contains some dots. For every aa and bb such that 1≤a≤b≤61≤a≤b≤6, there is exactly one domino with aa dots on one half and bb dots on the other half. The set contains exactly 2121 dominoes. Here is an exact illustration of his set:

Also, Anadi has an undirected graph without self-loops and multiple edges. He wants to choose some dominoes and place them on the edges of this graph. He can use at most one domino of each type. Each edge can fit at most one domino. It's not necessary to place a domino on each edge of the graph.

When placing a domino on an edge, he also chooses its direction. In other words, one half of any placed domino must be directed toward one of the endpoints of the edge and the other half must be directed toward the other endpoint. There's a catch: if there are multiple halves of dominoes directed toward the same vertex, each of these halves must contain the same number of dots.

How many dominoes at most can Anadi place on the edges of his graph?

Input

The first line contains two integers nn and mm (1≤n≤71≤n≤7, 0≤m≤n⋅(n−1)20≤m≤n⋅(n−1)2) — the number of vertices and the number of edges in the graph.

The next mm lines contain two integers each. Integers in the ii-th line are aiai and bibi (1≤a,b≤n1≤a,b≤n, a≠ba≠b) and denote that there is an edge which connects vertices aiai and bibi.

The graph might be disconnected. It's however guaranteed that the graph doesn't contain any self-loops, and that there is at most one edge between any pair of vertices.

Output

Output one integer which denotes the maximum number of dominoes which Anadi can place on the edges of the graph.

Examples

input

Copy

4 4
1 2
2 3
3 4
4 1

output

Copy

4

input

Copy

7 0

output

Copy

0

input

Copy

3 1
1 3

output

Copy

1

input

Copy

7 21
1 2
1 3
1 4
1 5
1 6
1 7
2 3
2 4
2 5
2 6
2 7
3 4
3 5
3 6
3 7
4 5
4 6
4 7
5 6
5 7
6 7

output

Copy

16

Note

Here is an illustration of Anadi's graph from the first sample test:

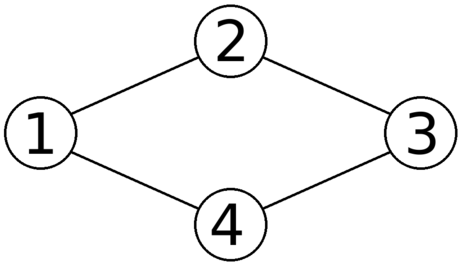
And here is one of the ways to place a domino on each of its edges:

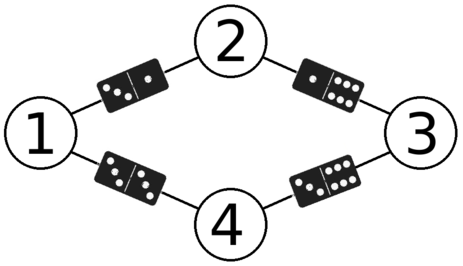
Note that each vertex is faced by the halves of dominoes with the same number of dots. For instance, all halves directed toward vertex 11have three dots.

题意：每条边可以加一个多米诺骨牌，但边连接着同一个节点时骨牌对应一边的数字也得相同，求最大可放置骨牌数。

在每个节点写入1-6的数（节点的值和数并不重要），那么66，11这种多米诺骨牌先不予考虑。

1，当N<=6时，最大的边数为15，恰好是除11，22之类的剩余骨牌数，每个节点对应一个数，可放置的骨牌即为边数。

2，当N==7时，此时多出了一个节点，那么还有一个节点必定要放重复的数，我们可以循环，假设循环的i，j节点代表的数字相等，找到所有相同数字节点所连接的最少顶点(数字相同的节点不可能连接同一个顶点)，然后删掉其中一半的边数。如果某个节点只连接一个节点，这种情况是不用删除的。

//by¡ªHonEy
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<vector>
using namespace std;
int n,m;
int x,y,ans;
int a[8][8];
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        ans=1000;
        memset(a,0,sizeof a);
        for(int i=1;i<=m;i++)
        {
            scanf("%d%d",&x,&y);
            a[x][y]=a[y][x]=1;
        }
        if(n<=6)
            printf("%d
",m);
        else
        {
            for(int i=1;i<7;i++)
            {
                for(int j=i+1;j<=7;j++)
                {
                    int cnt=0;
                    for(int k=1;k<=7;k++)
                    {
                        if(a[i][k]&&a[j][k])
                        {
                            cnt++;
                        }
                    }
                    ans=min(cnt,ans);
                }
            }
            printf("%d
",m-ans);
        }
    }
}