120. 三角形最小路径和
Difficulty: 中等
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-10<sup>4</sup> <= triangle[i][j] <= 10<sup>4</sup>
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
Solution
据说这道题是很久以前一道经典竞赛题目,给定一个“三角形”triangle,且triangle[i].length == triangle[i - 1].length + 1,“三角形”两个相邻的层,下一层总是比上一层多一个元素,第n层有n个元素。
题目规定“三角形”中的每一个点只能移动到下一层相邻的结点上,那么“三角形”第i行第j列结点处自顶向下的最小路径和f[i][j]就等于它上方两个结点处最小路径和的最小值加上“三角形”第i行第j列结点值,动态方程即min(f[i-1][j-1], f[i-1][j]) + triangle[i-1][j-1]。
解法一:因为要考虑到初始化的问题,我们创建(n+1)*(n+1)元素全部为零的矩阵f用于存放“三角形”每个节点处的最小路径和。初始矩阵的第一行和第一列都为零,我们直接从f的第二行第二列开始,对应“三角形”的第一行和第一列,因为是“三角形”的第一个元素所以此时的最小路径和就是结点处的值。然后还需要注意两个边界条件,就是当到了“三角形”的第i行的时候,如果此时元素在该层的头部(j==1),那么它的上一个来源结点只能是“三角形”中的(i-1,j),如果此时元素在该层的尾部(j==i),那么它的上一个来源结点只能是“三角形”中的(i-1,j-1),其余的情况则可能来自两个不同的地方。
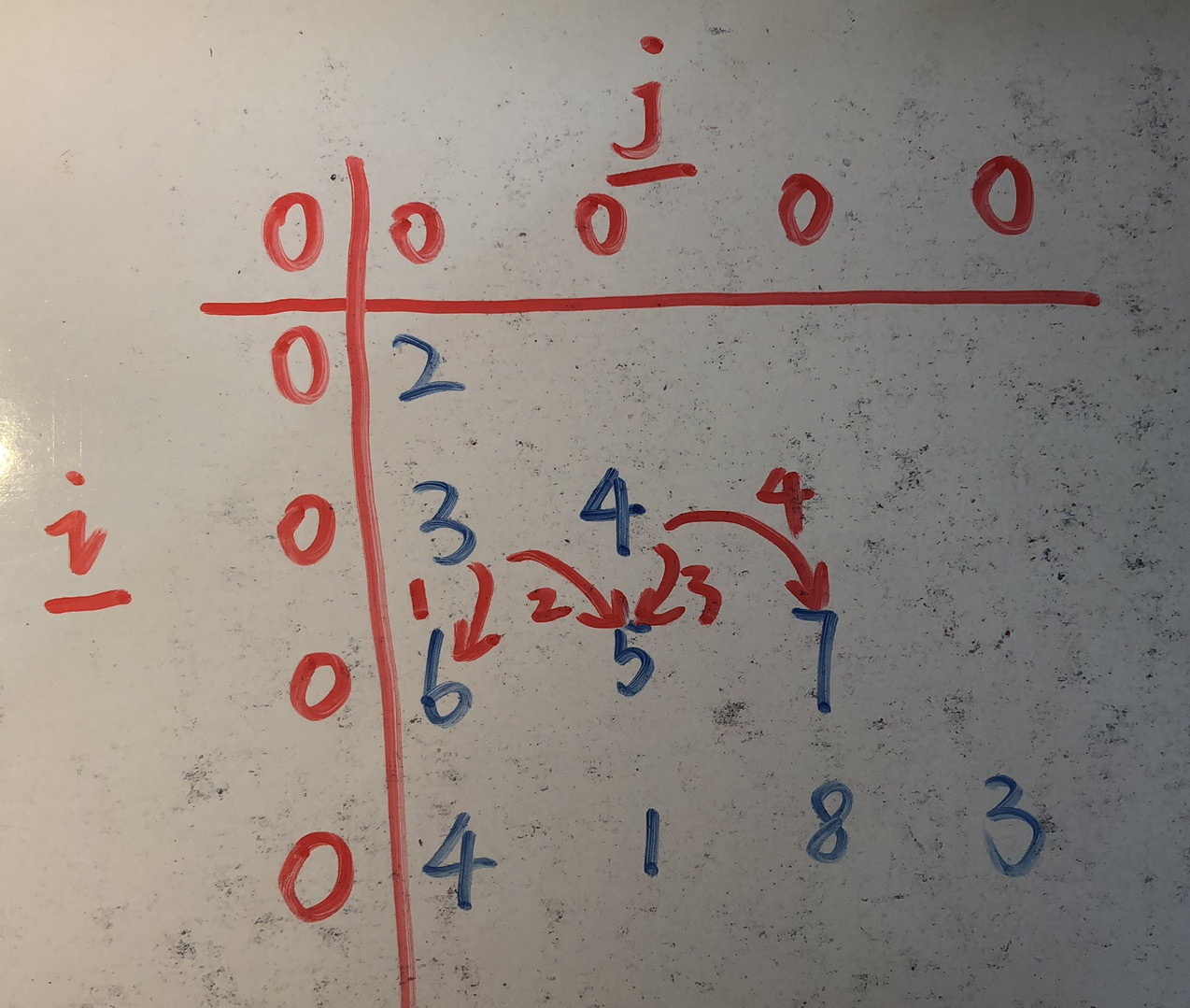
返回最后结果的时候需要注意,因为存储最小路径和的矩阵的第一列全部为0,在返回f最后一行的最小值需要把第一个元素排除掉。这种解法的时间复杂度和空间复杂度都为O(n^2)。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
f = [[0] * (n+1) for _ in range(n+1)]
for i in range(1, n + 1):
for j in range(1, i + 1):
if i == 1 and j == 1:
f[i][j] = triangle[i-1][j-1]
elif j == 1:
f[i][j] = f[i-1][j] + triangle[i-1][j-1]
elif j == i:
f[i][j] = f[i-1][j-1] + triangle[i-1][j-1]
else:
f[i][j] = min(f[i-1][j-1], f[i-1][j]) + triangle[i-1][j-1]
return min(f[n][1:])
解法二:空间优化,考虑到存储最小路径和的矩阵f每次更新的时候只用到了上一层,故只需要初始化一个2*(n+1)的矩阵来存储,每次更新完了之后做一次交换,最后返回结果的时候依照解法一就行了。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
f = [[0] * (n+1) for _ in range(2)]
for i in range(1, n + 1): # 行
for j in range(1, i + 1): # 列
if i == 1 and j == 1:
f[i][j] = triangle[i-1][j-1]
elif j == 1:
f[1][j] = f[0][j] + triangle[i-1][j-1]
elif j == i:
f[1][j] = f[0][j-1] + triangle[i-1][j-1]
else:
f[1][j] = min(f[0][j-1], f[0][j]) + triangle[i-1][j-1]
f[0], f[1] = f[1], f[0]
return min(f[0][1:])
解法三:进阶,只使用额外O(1)空间,直接在“三角形”内部更新,因为“三角形”结点处的最小路径和只与其上一层的元素有关,跟它左右相邻的元素无关,所以在更新自己结点处的最小路径和直接存放到“三角形”里面即可,不用额外的空间。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
for i in range(n):
for j in range(i+1):
if i == 0 and j == 0:
continue
elif j == 0:
triangle[i][j] += triangle[i-1][j]
elif j == i:
triangle[i][j] += triangle[i-1][j-1]
else:
triangle[i][j] += min(triangle[i-1][j], triangle[i-1][j-1])
return min(triangle[n-1])