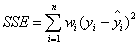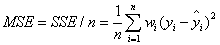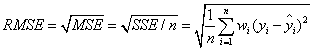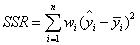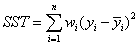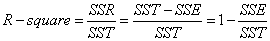SSE(和方差、误差平方和):The sum of squares due to error
MSE(均方差、方差):Mean squared error
RMSE(均方根、标准差):Root mean squared error
R-square(确定系数):Coefficient of determination
Adjusted R-square:Degree-of-freedom adjusted coefficient of determination
下面我对以上几个名词进行详细的解释下,相信能给大家带来一定的帮助!!
一、SSE(和方差)
该统计参数计算的是拟合数据和原始数据对应点的误差的平方和,计算公式如下
SSE越接近于0,说明模型选择和拟合更好,数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗,所以效果一样
二、MSE(均方差)
该统计参数是预测数据和原始数据对应点误差的平方和的均值,也就是SSE/n,和SSE没有太大的区别,计算公式如下
三、RMSE(均方根)
该统计参数,也叫回归系统的拟合标准差,是MSE的平方根,就算公式如下
在这之前,我们所有的误差参数都是基于预测值(y_hat)和原始值(y)之间的误差(即点对点)。从下面开始是所有的误差都是相对原始数据平均值(y_ba)而展开的(即点对全)!!!
四、R-square(确定系数)
在讲确定系数之前,我们需要介绍另外两个参数SSR和SST,因为确定系数就是由它们两个决定的
(1)SSR:Sum of squares of the regression,即预测数据与原始数据均值之差的平方和,公式如下
(2)SST:Total sum of squares,即原始数据和均值之差的平方和,公式如下
细心的网友会发现,SST=SSE+SSR,呵呵只是一个有趣的问题。而我们的“确定系数”是定义为SSR和SST的比值,故
其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1],越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好