谱聚类

谱聚类（Spectral Clustering,SC）是一种基于图论的聚类方法，将带权无向图划分为两个或两个以上的最优子图，使子图内部尽量相似，而子图间距离尽量远。能够识别任意形状的样本空间且收敛于全局最优解，基本思想是利用样本数据的相似矩阵（拉普拉斯矩阵）进行特征分解后得到的特征向量进行聚类。

对于item-user矩阵，如果要将item进行聚类

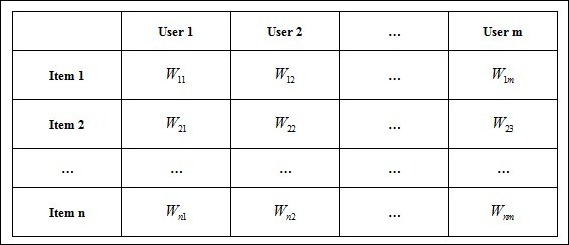
我们可以采用k-means聚类，复杂度为O(tknm),t为迭代次数，k为聚类个数，n为item个数，m为user个数。但显然，当M足够大、不知道聚类个数、类的假设不是球形等情形下k-means的缺陷倍显，且k-means不可避免的陷入局部最优。这使得聚类问题变得相当复杂，事实上，在各种现代聚类算法的比较中，K-means 通常都是作为 baseline 而存在的。

但是，如果我们计算出item和item间的相似度，便可以得到一个相似矩阵。将item看成节点，相似度看做边上的权重，便可以得到我们常见的图的概念。

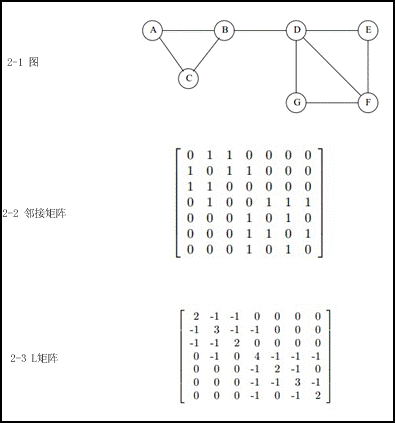
对于图的表示，如上图，常用的有邻接矩阵和Laplacian矩阵

谱聚类实现过程：

1. 构造相似度矩阵W
2. 把 的每一列元素加起来得到 个数，把它们放在对角线上（其他地方都是零），组成一个 的矩阵，记为 。并令
3. 求出 的前 个特征值（在本文中，除非特殊说明，否则“前 个”指按照特征值的大小从小到大的顺序） 以及对应的特征向量 。
4. 把这 个特征（列）向量排列在一起组成一个 的矩阵，将其中每一行看作 维空间中的一个向量，并使用 K-means 算法进行聚类。聚类的结果中每一行所属的类别就是原来 Graph 中的节点亦即最初的 个数据点分别所属的类别

最小割

一个经常被研究的问题就是 Graph Cut ，简单地说就是把一个 Graph 的一些边切断，让他被打散成一些独立联通的 sub-Graph ，而这些被切断的边的权值的总和就被称为 Cut 值。

直观上我们可以知道，权重比较大的边没有被切断，表示比较相似的点被保留在了同一个 sub-Graph 中，而彼此之间联系不大的点则被分割开来。我们可以认为这样一种分割方式是比较好的

参考资料：

1.http://blog.csdn.net/pi9nc/article/details/12251247

2.http://blog.sina.com.cn/s/blog_4b9b714a0100is4f.html