洛谷P1661 信息奥赛一本通1437：扩散

题目链接:

洛谷:https://www.luogu.com.cn/problem/P1661

信息奥赛一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid=1437

1437：扩散

时间限制: 1000 ms         内存限制: 65536 KB
提交数: 676     通过数: 347

【题目描述】

一个点每过一个单位时间就会向四个方向扩散一个距离，如图。

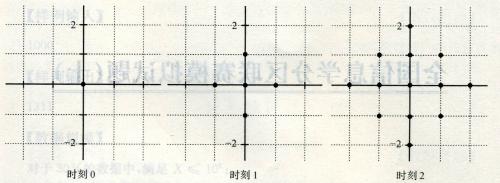
两个点a、b连通，记作e(a,b),当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、vu、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。给定平面上的n给点，问最早什么时刻它们形成一个连通块。

【输入】

第一行一个数n，以下n行，每行一个点坐标。

【输出】

一个数，表示最早的时刻所有点形成连通块。

【输入样例】

2
0 0
5 5

【输出样例】

5

【提示】

【数据规模】

对于20%的数据，满足1≤N≤5;1≤X[i],Y[i]≤501≤N≤5;1≤X[i],Y[i]≤50;

对于100%的数据，满足1≤N≤50;1≤X[i],Y[i]≤1091≤N≤50;1≤X[i],Y[i]≤109。

【来源】

No

对于这道题，先算出任意两点之间的曼哈顿距离，

然后将距离按从小到大排序，

之后对于每条边，用并查集查询是否已经合并，

求出需合并的最大边长度，

将他+1然后/2就得到答案。

代码：

#include<stdio.h>
struct node{
    int x,y;long long v;
}a[100001],by[100001];
int f[100001],n,lena,js;long long ans,x[100001],y[100001];
int find(int a1){return a1==f[a1]?a1:(f[a1]=find(f[a1]));}
long long abss(long long a1){return a1>=0?a1:(-a1);}
void px(int l,int r){
    if(l==r)return;
    int mid,i,j,p;
    mid=(l+r)/2;px(l,mid);px(mid+1,r);
    i=l;j=mid+1;p=l;
    while(i<=mid&&j<=r)
        if(a[i].v<a[j].v)by[p++]=a[i++];
        else by[p++]=a[j++];
    while(i<=mid)by[p++]=a[i++];
    while(j<=r)by[p++]=a[j++];
    for(i=l;i<=r;i++)a[i]=by[i];
    return;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d%d",x+i,y+i);
    for(int i=1;i<=n;i++)for(int j=1;j<i;j++)a[++lena]=(struct node){i,j,(abss(1ll*x[i]-x[j])+abss(1ll*y[i]-y[j]))};
    px(1,lena);
    for(int i=1;i<=n;i++)f[i]=i;
    for(int i=1;i<=lena&&js<n;i++)
        if(find(a[i].x)!=find(a[i].y)){js++;f[find(a[i].x)]=a[i].y;ans=a[i].v;}
    ans=(ans+1)/2;
    printf("%d",ans);
    return 0;
}