zoukankan html css js c++ java

总结「李超线段树」

转载注明来源：https://www.cnblogs.com/syc233/p/13722356.html

最近复习了李超线段树，发现网上不同人的写法有较大不同，所以写这篇博客总结一下自己的写法。

李超线段树是线段树的一个变种，支持在平面直角坐标系中动态插入线段，查询一条竖线与所有线段的交点纵坐标的最大值或最小值。

引入

P4097 [HEOI2013]Segment

题面

题意

要求在平面直角坐标系下维护两个操作：

在平面上加入一条线段。记第 (i) 条被插入的线段的标号为 (i)。
给定一个数 (k)，询问与直线 (l:x=k) 相交的线段中，交点纵坐标最大的线段的编号。

题解

李超线段树模板题。

对于线段树上每一个结点，维护一个区间最优线段。当一条线段满足以下条件时，它才能成为最优线段：

该线段的定义域覆盖整个区间。
该线段在区间中点处的值最大。

令区间 ([L,R]) 当前最优线段为 (l') ，考虑如何在区间 ([L,R]) 中插入线段 (l) ：

若当前区间没有最优线段，或者线段 (l') 被线段 (l) 完全覆盖（对于这道题，指线段 (l') 完全在插入线段下），那么线段 (l) 直接成为当前区间的最优线段。
若线段 (l) 被线段 (l') 完全覆盖 ~~一转攻势~~，那么线段 (l) 就没用了，不用再向下递归。
否则，线段 (l) 与线段 (l') 相交。令区间中点为 (mid) ，比较线段 (l) 和线段 (l') 在中点 (mid) 处的纵坐标大小，更新当前区间最优线段。

对于第三种情况，虽然线段 (l') 在当前区间中不再是最优线段了，但是它依然可能成为子区间的最优线段，代码实现中是交换线段 (l) 和线段 (l') ，用线段 (l') 更新子区间信息。

考虑如何更新子结点信息。令用来更新子区间信息的线段为 (l'') （因为上面更新过最优线段，所以线段 (l'') 一定是在 (mid) 处纵坐标较小的线段），对交点位置分类讨论：

若交点在 (mid) 左侧，如图：

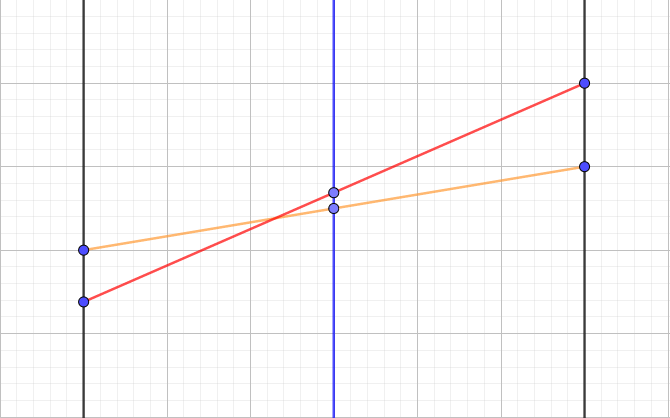
红色线段为当前最优线段，橙色线段为线段 (l'') ，此时线段 (l'') 只有可能在左子区间中成为最优线段，所以只需在线段树上更新左儿子的信息。
若交点在 (mid) 右侧，同理，更新右儿子信息。
若交点在 (mid) 处，若线段 (l'') 在 (L) 处的纵坐标较大，更新左儿子，否则更新右儿子。

查询时在线段树上二分找到这个位置，比较途径的所有区间的最优线段在这个位置时的纵坐标，取最大值即可。这其实是标记永久化的思想。

Code

用结构体封装一条线段：

struct line
{
	double k,b;// 斜率
	int id;    // 部分题需要记录线段编号
	line(double k=0,double b=0,int id=0):k(k),b(b),id(id){}
	inline double calcu(int pos)       // 计算线段在pos位置的纵坐标
	{
		return k*pos+b;
	}
	inline double cross(const line &T) // 求两条线段的交点横坐标
	{
		return (T.b-b)/(k-T.k);
	}
};

线段树结点：

struct node
{
	int l,r;   // 区间左右端点
	line L;    // 最优线段
	bool flag; // 记录区间内是否有最优线段
	node(int l,int r,line L,bool flag):l(l),r(r),L(L),flag(flag){}
	node(){}
}tree[maxn<<2];
#define ls (p<<1)   // 左儿子
#define rs (p<<1|1) // 右儿子

建树：

inline void build(int p,int l,int r)
{
	tree[p]=node(l,r,line(),false);
    // 新建一个没有最优线段的结点
	if(l==r) return;
	int mid=(l+r)>>1;
	build(ls,l,mid);
	build(rs,mid+1,r);
}

最重要的 ( ext{modify}) 操作：

这里并没有计算出交点横坐标，因为交点位置可以通过比较线段在端点处的纵坐标得出：

最优线段在 (mid) 处的取值一定较大，如果插入线段在左端点的取值较大，那么交点在左子区间，否则在右子区间。

这样计算同时也避免了多讨论交点在 (mid) 处的情况。

inline void modify(int p,int L,int R,line ln)
{
	int l=tree[p].l,r=tree[p].r;
	if(L<=l&&r<=R) // 如果插入线段的定义域覆盖整个区间
	{
		double lp=tree[p].L.calcu(l),rp=tree[p].L.calcu(r);
		double lq=ln.calcu(l),rq=ln.calcu(r);
        // 计算两条线段在区间端点的纵坐标
		if(!tree[p].flag) tree[p].L=ln,tree[p].flag=true;
		else if(lq-lp>eps&&rq-rp>eps) tree[p].L=ln;
        // 没有最优线段或者完全覆盖
		else if(lq-lp>eps||rq-rp>eps) // 相交
		{
			int mid=(l+r)>>1;
			if(ln.calcu(mid)-tree[p].L.calcu(mid)>eps) swap(tree[p].L,ln);
			if(ln.calcu(l)>tree[p].L.calcu(l))
				modify(ls,L,R,ln);
			else modify(rs,L,R,ln);
		}
	}
	else // 若未覆盖整个区间，检查子区间
	{
		int mid=(l+r)>>1;
		if(L<=mid) modify(ls,L,R,ln);
		if(R>mid) modify(rs,L,R,ln);
	}
}

查询：

typedef pair<double,int> pii;
inline pii query(int p,int pos) // 本题还要返回线段编号
{
	int l=tree[p].l,r=tree[p].r;
	double ans=tree[p].L.calcu(pos);
	int id=tree[p].L.id;
	if(l==r) return make_pair(ans,id);
	int mid=(l+r)>>1;
	if(pos<=mid)
	{
		pii lq=query(ls,pos);
		if(lq.first>ans||(fabs(lq.first-ans)<eps&&lq.second<id))
			ans=lq.first,id=lq.second;
	}
	else
	{
		pii rq=query(rs,pos);
		if(rq.first>ans||(fabs(rq.first-ans)<eps&&rq.second<id))
			ans=rq.first,id=rq.second;
	}
	return make_pair(ans,id);
}

复杂度分析

每次修改将区间分成 (log n) 个子区间，每个子区间的最优线段最多下放 (log n) 层，所以修改复杂度为 (O(log ^2n)) 。

每次查询经过 (log n) 个结点，复杂度 (O(log n)) 。

练习

P4254 [JSOI2008]Blue Mary开公司

一样的模板题，没什么好说的。

代码太丑了，就不贴了。

P4069 [SDOI2016]游戏

题面

题意

一棵树，有边权，每个点最初有一个极大数。

有两种操作：

修改，每次选定一条从 (s) 到 (t) 的路径，在这条路径上的每一个点上都添加一个数字。对于路径上的一个点 (r) ，若 (r) 与 (s) 的距离是 (dis) ，那么在点 (r) 上添加的数字是 (a imes dis+b)。
查询，选定一条从 (s) 到 (t) 的路径，查询路径上的最小数字。

题解

修改操作类似于添加一条直线，考虑如何才能用李超线段树维护题目中所给的信息。

设点 (u) 到根的距离为 (dis_u) ，令 (s) 和 (t) 在树上的 LCA 为 (x) 。把每次修改的路径分为两段：

对于路径 (s o x) 上的点 (r) ，添加的数字是 (a imes (dis_s-dis_r)+b=-a imes dis_r+a imes dis_s+b) ，这是一条以 (dis_r) 为横坐标，斜率为 (-a) ，截距为 (a imes dis_s +b) 的线段。
对于路径 (x o t) 上的点 (r) ，添加的数字是 (a imes (dis_s-dis_x+dis_r-dis_x)+b=a imes dis_r+a imes (dis_s-2 imes dis_x)+b) ，这是一条以 (dis_r) 为横坐标，斜率为 (a) ，截距为 (a imes (dis_s-2 imes dis_x)+b) 的线段。

于是树剖+李超线段树维护横坐标为 (dis_u) 的线段即可。

( ext{Code}:)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
#define maxn 100005
#define Rint register int
using namespace std;
typedef long long lxl;
const lxl INF=123456789123456789ll;

template <typename T>
inline void read(T &x)
{
	x=0;T f=1;char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
	x*=f;
}

struct edge
{
	int u,v,w,next;
}e[maxn<<1];

int head[maxn],k;

inline void add(int u,int v,int w)
{
	e[k]=(edge){u,v,w,head[u]};
	head[u]=k++;
}

int n,m;
int dfn[maxn],idx[maxn],dep[maxn],top[maxn],fa[maxn],siz[maxn],son[maxn],dfs_cnt;
lxl dis[maxn];

inline void dfs1(int u,int fath)
{
	dep[u]=dep[fa[u]=fath]+1;
	siz[u]=1;
	son[u]=-1;
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa[u]) continue;
		dis[v]=dis[u]+e[i].w;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(!~son[u]||siz[v]>siz[son[u]]) son[u]=v;
	}
}

inline void dfs2(int u,int t)
{
	top[u]=t;
	dfn[u]=++dfs_cnt;
	idx[dfs_cnt]=u;
	if(!~son[u]) return;
	dfs2(son[u],t);
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa[u]||v==son[u]) continue;
		dfs2(v,v);
	}
}

inline int LCA(int a,int b)
{
	while(top[a]!=top[b])
	{
		if(dep[top[a]]<dep[top[b]]) swap(a,b);
		a=fa[top[a]];
	}
	return dep[a]<dep[b] ? a : b;
}

struct line
{
	lxl k,b;
	line(lxl k=0,lxl b=0):k(k),b(b){}
	inline lxl calcu(int pos)
	{
		return k*dis[idx[pos]]+b;
	}
};

struct Segment_Tree
{
	struct node
	{
		int l,r;
		line L;
		lxl Min;
		node(int l,int r,line L,lxl Min):l(l),r(r),L(L),Min(Min){}
		node(){}
	}tree[maxn<<2];
	#define ls (p<<1)
	#define rs (p<<1|1)
	inline void update(int p)
	{
		tree[p].Min=min(tree[p].Min,min(tree[ls].Min,tree[rs].Min));
	}
	inline void build(int p,int l,int r)
	{
		tree[p]=node(l,r,line(0,INF),INF);
		if(l==r) return;
		int mid=(l+r)>>1;
		build(ls,l,mid);
		build(rs,mid+1,r);
		update(p);
	}
	inline void modify(int p,int L,int R,line ln)
	{
		int l=tree[p].l,r=tree[p].r;
		if(L<=l&&r<=R)
		{
			lxl lp=tree[p].L.calcu(l),rp=tree[p].L.calcu(r);
			lxl lq=ln.calcu(l),rq=ln.calcu(r);
			if(lq<=lp&&rq<=rp)
			{
				tree[p].L=ln;
				tree[p].Min=min(tree[p].Min,min(tree[p].L.calcu(l),tree[p].L.calcu(r)));
			}
			else if(lq<=lp||rq<=rp)
			{
				int mid=(l+r)>>1;
				if(ln.calcu(mid)<tree[p].L.calcu(mid)) swap(ln,tree[p].L);
				if(ln.calcu(l)<tree[p].L.calcu(l))
					modify(ls,L,R,ln);
				else modify(rs,L,R,ln);
				tree[p].Min=min(tree[p].Min,min(tree[p].L.calcu(l),tree[p].L.calcu(r)));
				update(p);
			}
		}
		else
		{
			int mid=(l+r)>>1;
			if(L<=mid) modify(ls,L,R,ln);
			if(R>mid) modify(rs,L,R,ln);
			update(p);
		}
	}
	inline lxl query(int p,int L,int R)
	{
		int l=tree[p].l,r=tree[p].r;
		if(L<=l&&r<=R) return tree[p].Min;
		lxl lx=max(l,L),rx=min(r,R);
		lxl ans=min(tree[p].L.calcu(lx),tree[p].L.calcu(rx));
		int mid=(l+r)>>1;
		if(L<=mid) ans=min(ans,query(ls,L,R));
		if(R>mid) ans=min(ans,query(rs,L,R));
		return ans;
	}
}st;

inline void modify(int u,int v,line ln)
{
	for(;top[u]!=top[v];u=fa[top[u]])
		st.modify(1,dfn[top[u]],dfn[u],ln);
	st.modify(1,dfn[v],dfn[u],ln);
}

inline lxl query(int u,int v)
{
	lxl res=INF;
	for(;top[u]!=top[v];u=fa[top[u]])
		res=min(res,st.query(1,dfn[top[u]],dfn[u]));
	res=min(res,st.query(1,dfn[v],dfn[u]));
	return res;
}

int main()
{
	// freopen("P4069.in","r",stdin);
	read(n),read(m);
	memset(head,-1,sizeof(head));
	for(int i=1,u,v,w;i<n;++i)
	{
		read(u),read(v),read(w);
		add(u,v,w);
		add(v,u,w);
	}
	dfs1(1,0);
	dfs2(1,1);
	st.build(1,1,n);
	int opt,s,t,a,b;
	while(m--)
	{
		read(opt),read(s),read(t);
		int x=LCA(s,t);
		if(opt==1)
		{
			read(a),read(b);
			modify(s,x,line(-a,a*dis[s]+b));
			modify(t,x,line(a,a*(dis[s]-2*(dis[x]))+b));
		}
		else
		{
			lxl res1=query(s,x);
			lxl res2=query(t,x);
			printf("%lld
",min(res1,res2));
		}
	}
	return 0;
}

P4655 [CEOI2017]Building Bridges

题面

题意

有 (n) 根柱子依次排列，每根柱子都有一个高度。第 (i) 根柱子的高度为 (h_i) 。

现在想要建造若干座桥，如果一座桥架在第 (i) 根柱子和第 (j) 根柱子之间，那么需要 ((h_i-h_j)^2) 的代价。

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 ii 根柱子被拆除的代价为 (w_i) ，注意 (w_i) 不一定非负，因为可能政府希望拆除某些柱子。

现在政府想要知道，通过桥梁把第 (1) 根柱子和第 (n) 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

题解

~~一眼DP题~~

尝试写出DP转移方程，令 (f_i) 表示使用第 (i) 根柱子的最小代价（只考虑 (1 sim i) 的柱子），则有转移方程：

[f_i=min_{1leq j <i}{f_j+(h_i-h_j)^2-sum_{k=j+1}^{i-1}w_k} ]

令 (sum_i=sum_{j=1}^i w_j) ，则：

[egin{aligned} f_i&=min_{1leq j <i}{f_j+(h_i-h_j)^2+(sum_{i-1}-sum_j)}\ &=min_{1leq j <i}{f_j-2h_ih_j+h_j^2-sum_j}+h_i^2+sum_{i-1} end{aligned} ]

发现这好像可以斜率优化，于是假设 (k) 比 (j) 优：

[egin{aligned} f_k-2h_ih_k+h_k^2-sum_k&<f_j-2h_ih_j+h_j^2-sum_j\ (f_k+h_k^2-sum_k)-(f_j+h_j^2-sum_j)&<2h_i(h_k-h_j)\ frac{(f_k+h_k^2-sum_k)-(f_j+h_j^2-sum_j)}{(h_k-h_j)}&<2h_i end{aligned} ]

~~所以这和我李超线段树有什么关系呢~~

发现 (h_i) 和 (sum_i) 均不单调，那怎么办呢。

~~平衡树维护动态凸包~~

~~CDQ分治维护凸包~~

我们再看一下DP转移方程：

[egin{aligned} f_i&=min_{1leq j <i}{f_j-2h_ih_j+h_j^2-sum_j}+h_i^2+sum_{i-1}\ &=min_{1leq j <i}{(-2h_j)h_i+(f_j+h_j^2-sum_j)}+h_i^2+sum_{i-1} end{aligned} ]

这东西是不是有亿点熟悉。

相当于有一些斜率为 (-2h_j) ，截距为 (f_j+h_j^2-sum_j) 的直线，查询横坐标为 (h_i) 时直线纵坐标的最小值。

那么这道题就简单了，只需要用李超线段树支持平面插入直线，查询某个横坐标处所有直线纵坐标的最小值即可。

( ext{Code}:)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define maxn 100005
#define maxm 1000005
#define Rint register int
#define INF 0x3f3f3f3f
using namespace std;
typedef long long lxl;

template <typename T>
inline void read(T &x)
{
	x=0;T f=1;char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
	x*=f;
}

int n;
lxl h[maxn],sum[maxn],f[maxn];

struct line
{
	lxl k,b;
	line(lxl k=0,lxl b=0):k(k),b(b){}
	inline lxl calcu(lxl pos)
	{
		return k*pos+b;
	}
};

struct Segment_Tree
{
	struct node
	{
		int l,r;
		line L;
		node(int l,int r,line L):l(l),r(r),L(L){}
		node(){}
	}tree[maxm<<2];
	#define ls (p<<1)
	#define rs (p<<1|1)
	inline void build(int p,int l,int r,line ln)
	{
		tree[p]=node(l,r,ln);
		if(l==r) return;
		int mid=(l+r)>>1;
		build(ls,l,mid,ln);
		build(rs,mid+1,r,ln);
	}
	inline void modify(int p,int L,int R,line ln)
	{
		int l=tree[p].l,r=tree[p].r;
		if(L<=l&&r<=R)
		{
			lxl lp=tree[p].L.calcu(l),rp=tree[p].L.calcu(r);
			lxl lq=ln.calcu(l),rq=ln.calcu(r);
			if(lp<=lq&&rp<=rq) return;
			else if(lp>=lq&&rp>=rq) tree[p].L=ln;
			else
			{
				int mid=(l+r)>>1;
				if(ln.calcu(mid)<tree[p].L.calcu(mid)) swap(tree[p].L,ln);
				if(ln.calcu(l)<tree[p].L.calcu(l)) modify(ls,L,R,ln);
				else modify(rs,L,R,ln);
			}
		}
		else
		{
			int mid=(l+r)>>1;
			if(L<=mid) modify(ls,L,R,ln);
			if(R>mid) modify(rs,L,R,ln);
		}
	}
	inline lxl query(int p,int ps)
	{
		int l=tree[p].l,r=tree[p].r;
		if(l==r) return tree[p].L.calcu(ps);
		int mid=(l+r)>>1;
		lxl ans=tree[p].L.calcu(ps);
		if(ps<=mid) ans=min(ans,query(ls,ps));
		else ans=min(ans,query(rs,ps));
		return ans;
	}
}st;

int main()
{
	// freopen("P4655.in","r",stdin);
	read(n);
	for(int i=1;i<=n;++i) read(h[i]);
	for(int i=1,w;i<=n;++i)
	{
		read(w);
		sum[i]=sum[i-1]+w;
	}
	f[1]=0;
	st.build(1,1,1e6,line(-2*h[1],f[1]+h[1]*h[1]-sum[1]));
	for(int i=2;i<=n;++i)
	{
		f[i]=st.query(1,h[i])+h[i]*h[i]+sum[i-1];
		st.modify(1,1,1e6,line(-2*h[i],f[i]+h[i]*h[i]-sum[i]));
	}
	printf("%lld
",f[n]);
	return 0;
}

CF932F Escape Through Leaf

题面

题意

一棵根为 (1) 的树，每个点有两个权值 (a_u,b_u) 。

每次可以从点 (u) 跳到它子树中任意一个点 (v) ，费用为 (a_u imes b_v) 。

求每一个点跳到叶节点的最小花费。

题解

令 (f_u) 表示从点 (u) 跳到叶节点的最小花费，则有转移方程：

[f_u=min_{vin subtree_u}{a_u imes b_v+f_v} ]

相当于每次查询一堆斜率为 (b_v) ，截距为 (f_v) 的直线在 (a_u) 处的最小取值。

因为在树上，所以线段树合并即可。

( ext{Code}:)

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define maxn 100005
#define Rint register int
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long lxl;
const lxl M=1e5+1;

template <typename T>
inline void read(T &x)
{
	x=0;T f=1;char ch=getchar();
	while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
	x*=f;
}

struct edge
{
	int u,v,next;
	edge(int u,int v,int next):u(u),v(v),next(next){}
	edge(){}
}e[maxn<<1];

int head[maxn],k;

inline void add(int u,int v)
{
	e[k]=edge(u,v,head[u]);
	head[u]=k++;
}

int n;

struct line
{
	lxl k,b;
	bool flag;
	line(lxl k=0,lxl b=0,bool flag=0):k(k),b(b),flag(flag){}
	inline lxl calcu(int pos)
	{
		if(!flag) return INF;
		return k*(pos-M)+b;
	}
}tree[maxn<<3];

int rt[maxn],tot,ch[maxn<<3][2];

inline void modify(int &p,int l,int r,int L,int R,line ln)
{
	if(!p) p=++tot;
	if(L<=l&&r<=R)
	{
		lxl lp=tree[p].calcu(l),rp=tree[p].calcu(r);
		lxl lq=ln.calcu(l),rq=ln.calcu(r);
		if(!tree[p].flag) tree[p]=ln;
		else if(lq<=lp&&rq<=rp) tree[p]=ln;
		else if(lq<=lp||rq<=rp)
		{
			int mid=(l+r)>>1;
			if(ln.calcu(mid)<tree[p].calcu(mid)) swap(ln,tree[p]);
			if(ln.calcu(l)<tree[p].calcu(l))
				modify(ch[p][0],l,mid,L,R,ln);
			else modify(ch[p][1],mid+1,r,L,R,ln);
		}
	}
	else
	{
		int mid=(l+r)>>1;
		if(L<=mid) modify(ch[p][0],l,mid,L,R,ln);
		if(R>mid) modify(ch[p][1],mid+1,r,L,R,ln);
	}
}

inline lxl query(int p,int l,int r,int ps)
{
	if(!p) return INF;
	lxl ans=tree[p].calcu(ps);
	if(l==r) return ans;
	int mid=(l+r)>>1;
	if(ps<=mid) return min(ans,query(ch[p][0],l,mid,ps));
	else return min(ans,query(ch[p][1],mid+1,r,ps));
}

inline int merge(int x,int y,int l,int r)
{
	if(!x||!y) return x|y;
	int mid=(l+r)>>1;
	ch[x][0]=merge(ch[x][0],ch[y][0],l,mid);
	ch[x][1]=merge(ch[x][1],ch[y][1],mid+1,r);
	modify(x,l,r,l,r,tree[y]);
	return x;
}

lxl a[maxn],b[maxn];
lxl f[maxn];

inline void dfs(int u,int fa)
{
	for(int i=head[u];~i;i=e[i].next)
	{
		int v=e[i].v;
		if(v==fa) continue;
		dfs(v,u);
		rt[u]=merge(rt[u],rt[v],1,M<<1);
	}
	if(rt[u])
		f[u]=query(rt[u],1,M<<1,a[u]);
	modify(rt[u],1,M<<1,1,M<<1,line(b[u],f[u],true));
}

int main()
{
	// freopen("CF932F.in","r",stdin);
	read(n);
	for(int i=1;i<=n;++i) read(a[i]),a[i]+=M;
	for(int i=1;i<=n;++i) read(b[i]);
	memset(head,-1,sizeof(head));
	for(int i=1,u,v;i<n;++i)
	{
		read(u),read(v);
		add(u,v);
		add(v,u);
	}
	dfs(1,0);
	for(int i=1;i<=n;++i)
		printf("%lld ",f[i]);
	return 0;
}

参考资料

李超线段树 - OI Wiki

算法｜李超线段树初步（算法讲解+例题）

查看全文

相关阅读:
Springboot操作域对象
 Thymeleaf的条件判断和迭代遍历
 Thymeleaf的字符串与变量输出的操作
 window 2003 实现多用户远程登录
 非常漂亮js动态球型云标签特效代码
 Echarts运用
 sass、less和stylus的安装使用和入门实践
 java,js 解unicode
Java上传下载excel、解析Excel、生成Excel
小知识点应用

原文地址：https://www.cnblogs.com/syc233/p/13722356.html