题目:

思路:
把时间当做距离利用Dijkstra算法来做这个题。
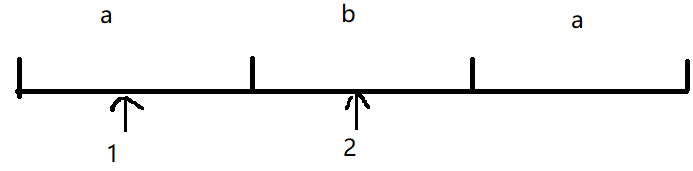
前提:该结点e.c<=e.a,k = d[v]%(e.a+e.b);
当车在这个点的1处时,如果在第一个a这段时间内能够通过且更小的话,那时间就更新为d[e.to] = d[v]+e.a-k+e.c;
当车在这个点的1处时,如果在第一个a这段时间内不能通过,但等待之后再通过时间更短的话,那时间更新为d[e.to]=d[v]+e.a+e.b-k+e.c
如果在这个点的2处时,如果在等待之后通过的时间更短的话,时间更新和第二种情况一样为d[e.to]=d[v]+e.a+e.b-k+e.c
所有的边是有向边,然后用迪杰斯特拉算法解题就可以了。
代码:
#include <bits/stdc++.h> #define inf 0x3f3f3f3f #define MAX 1000000000 #define mod 1000000007 #define FRE() freopen("in.txt","r",stdin) #define FRO() freopen("out.txt","w",stdout) using namespace std; typedef long long ll; typedef pair<int,int> P;//first-距离 second-编号 const int maxn = 505; int d[maxn]; int n,m,s,t; struct Edge { int to,a,b,c; }; vector<Edge> G[maxn*100]; void init() { for(int i=0; i<maxn*100; i++) { G[i].clear(); if(i<maxn) { d[i] = inf; } } for(int i=0; i<m; i++) { int u,v,a,b,c; scanf("%d%d%d%d%d",&u,&v,&a,&b,&c); G[u].push_back(Edge{v,a,b,c}); } } void Dijstra(){ priority_queue<P,vector<P>,greater<P> > que; d[s] = 0; que.push(P(0,s)); while(!que.empty()){ P p = que.top();que.pop(); int v = p.second; // cout<<"GG "<<v<<endl; if(d[v]>p.first) continue; //cout<<"size: "<<G[v].size()<<endl; for(int i=0; i<G[v].size(); i++){ Edge e = G[v][i]; int k = d[v]%(e.a+e.b); if(k+e.c<=e.a && d[e.to]>d[v]+e.c && e.c<=e.a){ d[e.to] = d[v]+e.c; que.push(P(d[e.to],e.to)); //cout<<"Fuck!"<<endl; }else if(k+e.c>e.a && d[e.to]>d[v]+e.a+e.b-k+e.c && e.c<=e.a){ d[e.to] = d[v]+e.a+e.b-k+e.c; que.push(P(d[e.to],e.to)); //cout<<"Fuck!"<<endl; } } } } int main() { // FRE(); int kase=0; while(scanf("%d%d%d%d",&n,&m,&s,&t)!=EOF) { init(); Dijstra(); printf("Case %d: %d ",++kase,d[t]); } return 0; }