Cat VS Dog HDU_3829（最大独立集最大匹配）

Cat VS Dog

题意：一群小朋友去动物园，如果每个小朋友喜欢的动物是猫，那么不喜欢的动物一定是狗，反之也是。现在动物园的管理者要拿走一些动物，如果拿走的是某个小朋友不喜欢的动物，那这个小朋友就非常开心，反之，如果是某个小朋友喜欢的动物，这个小朋友就非常的不开心，问那完后最多有几个小朋友会非常开心。

暑假最后一场个人赛，可还行，有点凉凉~~

讲真看出是二分图最大匹配的题目，但是没学最大独立集，死活建不出图来，就到底还是自己的能力不行啊！

最小覆盖：

定义：假如选了一个点就相当于覆盖了以它为端点的所有边。最小顶点覆盖就是选择最少的点来覆盖所有的边。

求解方法：最小顶点覆盖等于二分图的最大匹配。

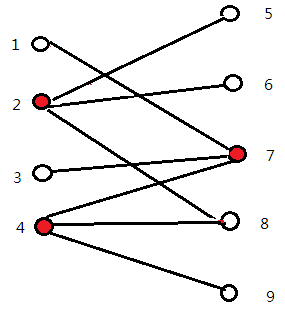
看定义~~~~~~不懂，找了找图，照着一对比，明白了。放图

很对！没错！！最小顶点覆盖就是3，符合条件的点就是图中的{2,4,7}

最大独立集：

定义：选出一些顶点使得这些顶点两两不相邻，则这些点构成的集合称为独立集。找出一个包含顶点数最多的独立集称为最大独立集。

求解方法：最大独立集 = 顶点个数 - 最小覆盖

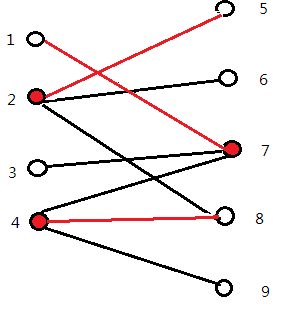
看了定义依旧不懂，脑子是个好东西啊，还是上边的图，再结合题意，有点懂了，关门放图~~

​

图中的红线是最大匹配的结果所以经过最大匹配后得到的最小覆盖是3，而筛选出来的顶点有{2,4,7}，那剩下的就是最大独立集{1,3,5,6,8,9}

思路：看完知识点来解一下思路吧。将每个小朋友喜欢的动物和不喜欢的动物保存起来，遍历，如果这个小朋友喜欢的动物是另一个小朋友不喜欢的动物就在这两个之间画一条线。求最小覆盖（最大匹配），此时用总共的点数减去这个最小覆盖得结果就是高兴的小朋友的最大人数。

代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <queue>
#include <vector>
#include <algorithm>
#define FRE() freopen("in.txt","r",stdin)
#define INF 0x3f3f3f3f

using namespace std;
typedef long long ll;
const int maxn = 600;
int mp[maxn][maxn],link[maxn],vis[maxn];
string like[maxn];
string dislike[maxn];
int n,m,p;

bool dfs(int x)
{
    for(int i = 0; i < p; i++)
    {
        if(!vis[i] && mp[x][i])
        {
            vis[i] = 1;
            if(link[i] == 0 || dfs(link[i]))
            {
                link[i] = x;
                return true;
            }
        }
    }
    return false;
}

int hunary()
{
    int res = 0;
    memset(link,0,sizeof(link));
    for(int i = 0; i < p; i++)
    {
        memset(vis,0,sizeof(vis));
        if(dfs(i))
            res++;
    }
    return res;
}

int main()
{
    while(scanf("%d%d%d",&n,&m,&p) != EOF)
    {
        for(int i = 0; i < p; i++)
            cin>>like[i]>>dislike[i];

        memset(mp, 0, sizeof(mp));
        for(int i = 0; i < p; i++)
        for(int j = 0; j < p; j++)
        {
            if(like[i].compare(dislike[j]) == 0 || like[j].compare(dislike[i]) == 0)
                mp[i][j] = 1;
        }
        int res = hunary();
        printf("%d
",p - res/2);
    }
    return 0;
}