匈牙利算法求最大匹配（HDU-4185 Oil Skimming）

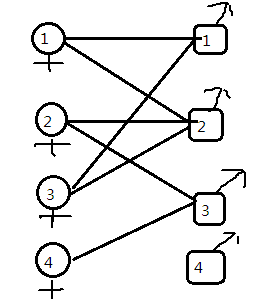
如下图：要求最多可以凑成多少对对象

大佬博客：

https://blog.csdn.net/cillyb/article/details/55511666

https://blog.csdn.net/denghecsdn/article/details/77619308

https://www.cnblogs.com/wangjunyan/p/5563154.html

模板：

int link[maxn],vis[maxn];
bool dfs(int x)
{
    for(int i = 1; i <= num; i++)
    {
        if(!vis[i] && cp[x][i])
        {
            vis[i] = 1;
            if(link[i] == 0 || dfs(link[i]))
            {
                link[i] = x;
                return true;
            }
        }
    }
    return false;
}

int hunyary()
{
    int sum = 0;
    memset(link, 0, sizeof(link));
    for(int i = 1; i <= num; i++)
    {
        memset(vis, 0, sizeof(vis));
        if(dfs(i))
            sum++;
    }
    return sum;
}

最后的sum值就是最大的匹配值。

附练习题：HDU-4185 Oil Skimming

水平和竖直的两个‘#’，可以连成一条边，求这样的边最多有多少条。

主要是自己如何去建图：

1. 遍历数组mp对‘#’进行标号；
2. 再次遍历遇到‘#’，看他上下左右是否有‘#’，有的话在cp数组中进行连线；
3. 再利用匈牙利算法求最大匹配。

代码：

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <queue>
#include <vector>
#include <algorithm>
#define FRE() freopen("in.txt","r",stdin)
#define INF 0x3f3f3f3f

using namespace std;
typedef long long ll;
const int maxn = 605;
int n,k,cnt = 0,num;
char mp[maxn][maxn];
int temp[maxn][maxn],cp[maxn][maxn];
int link[maxn],vis[maxn];

inline void init()
{
    memset(temp, 0, sizeof(temp));
    memset(cp, 0, sizeof(cp));
}

bool dfs(int x)
{
    for(int i = 1; i <= num; i++)
    {
        if(!vis[i] && cp[x][i])
        {
            vis[i] = 1;
            if(link[i] == 0 || dfs(link[i]))
            {
                link[i] = x;
                return true;
            }
        }
    }
    return false;
}

int hunyary()
{
    int sum = 0;
    memset(link, 0, sizeof(link));
    for(int i = 1; i <= num; i++)
    {
        memset(vis, 0, sizeof(vis));
        if(dfs(i))
            sum++;
    }
    return sum;
}


int main()
{
    //FRE();
    scanf("%d",&k);
    while(k--)
    {
        init();
        scanf("%d",&n);
        for(int i = 0; i < n; i++)
            scanf("%s",mp[i]);

        num = 0;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(mp[i][j] == '#')
                    temp[i][j] = ++num;
            }
        }

        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(mp[i][j] == '#')
                {
                    if(i - 1 >= 0 && mp[i-1][j] == '#') cp[temp[i][j]][temp[i-1][j]] = 1;
                    if(i + 1 < n && mp[i+1][j] == '#') cp[temp[i][j]][temp[i+1][j]] = 1;
                    if(j - 1 >= 0 && mp[i][j-1] == '#') cp[temp[i][j]][temp[i][j-1]] = 1;
                    if(j + 1 < n && mp[i][j+1] == '#') cp[temp[i][j]][temp[i][j+1]] = 1;
                }

            }
        }
        int res = hunyary();
        printf("Case %d: %d
",++cnt, res / 2);
    }
    return 0;
}