康拓展开

原理：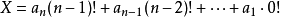

举个例子来说明康拓展开的应用：

已知1,2,3,4,5五个数的全排列，给出一个排列34152，问该排列在全排列中是第几个。而康托展开的值就是这个排名。

• 首位是3，比它小而且没有出现过的数有1,2两个，所以为          2 * 4！；
• 第二位是4，比它小而且没有出现过的数有1,2两个，所以值为  2 * 3！；
• 第三位是1，没有比它小而且没有出现过的数，所以值为            0 * 2！；
• 第四位是5，比它小而且没有出现过的数有2一个，所以值为     1  * 1 ！；
• 第五位是2，没有比它小而且没有出现过的数，所以值为            0  *  0！；

最终相加的结果是61，所以34152在全排列中是第61个。

实现的代码为：

int FAC[20];   // 阶乘
int cantor(int *a, int n)
{
    FAC[1] = 1;
    for(int i = 1; i <= 20; i++)//求阶乘
        FAC[i] = FAC[i-1] * i;
    int x = 0;
    for (int i = 0; i < n; ++i) {
        int smaller = 0;  // 在当前位之后小于其的个数，这里很神奇，
        for (int j = i + 1; j < n; ++j) {//最终的结果就是小于该数却没有出现过的数的个数
            if (a[j] < a[i])
                smaller++;
        }
        x += FAC[n - i - 1] * smaller; // 康托展开累加
    }
    return x;  // 康托展开值
}
/*这里在求小于该数却没有出现过的数的时候，如果n很大就会有超时的危险，可以用线段树来实现*/

或

int FAC[20];   // 阶乘
int vis[maxn];
int cantor(int *a, int n)
{
    FAC[1] = 1;
    for(int i = 1; i <= 20; i++)//求阶乘
        FAC[i] = FAC[i-1] * i;
    int x = 0;
    for (int i = 0; i < n; ++i) {
        int smaller = 0; 
        vis[a[i]] = 1;
        for (int j = 0; j < i; ++j) {
            if (!vis[j] && a[j] < a[i])
                smaller++;
        }
        x += FAC[n - i - 1] * smaller; // 康托展开累加
    }
    return x;  // 康托展开值
}
/*从前边开始的统计如上*/