Codeforces Round #699 (Div.2)
六道题,考场上只过了ABC,C题样例不够强,随机的也太弱,被C题卡了好久,还是太菜了
CF1481A Space Navigation
题意:最开始在((0,0)),给出一串往上下左右走的操作序列,可以删掉一些操作,问是否能走到((x,y))。
由于可以无限删,所以对四个象限分别讨论,对于每个象限都有两种操作是不需要的,统计剩下两个看够不够走到即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 200005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T;
char ch[N];
int main()
{
T=read();
while(T--)
{
int x=read(),y=read(),R=0,U=0,D=0,L=0;
scanf("%s",(ch+1));
int len=strlen(ch+1);
for(int i=1;i<=len;i++)R+=(ch[i]=='R'),U+=(ch[i]=='U'),D+=(ch[i]=='D'),L+=(ch[i]=='L');
if(x>=0&&y>=0&&x<=R&&y<=U)puts("YES");
else if(x<0&&y>=0&&-x<=L&&y<=U)puts("YES");
else if(x>=0&&y<0&&x<=R&&-y<=D)puts("YES");
else if(x<0&&y<0&&-x<=L&&-y<=D)puts("YES");
else puts("NO");
}
return 0;
}
CF1481B New Colony
题意:每次在第一个位置放一个石头,如果(h_{i+1}>h_i)则石头会往下滚,如果到了位置(n)则会滚入回收系统,否则让所在位置的(h)增加(1),求第(k)次扔石头会停在哪里
小模拟,因为(h_ileq100),因此填满次数不会很大,当他填满后之后放的所有石头都会滚入回收系统,因此直接枚举到滚入回收系统之前即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 105
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T,n,k,a[N];
int main()
{
T=read();
while(T--)
{
n=read();k=read();
int ans;
for(int i=1;i<=n;i++)a[i]=read();
a[n+1]=0;
for(int i=1;i<=k;i++)
{
int pos=1;
while(pos<=n)
{
if(a[pos]<a[pos+1])break;
pos++;
}
if(pos==n+1){ans=-1;break;}
else a[pos]++;
if(i==k)ans=pos;
}
//puts("---------");
//for(int i=1;i<=n;i++)printf("%d ",a[i]);
//puts("");
//puts("---------");
printf("%d
",ans);
}
return 0;
}
CF1481C Fence Painting
题意:有(n)个位置,最开始每个位置颜色为(a_i),你要把它染成(b_i),现在有(m)个画师依次来染色,第(i)个画师需要你帮他找一个位置让他把这个位置的颜色染成(c_i),问是否有解,输出方案。
坑爹题,卡了半个小时。
首先可以想到就是倒序处理,因为倒序处理一旦决定一个地方染色了,这个地方在这个时间点之前怎么染就无所谓了。
因此考虑把所有(a_i)和(b_i)不同的地方都塞进一个(vector)里,然后把每个颜色的画师塞到对应颜色的(vector)中,一旦某个地方没有画师了那就不合法,然后剩下的画师随便找地方画即可,如果最后一个画师没地方画了也不合法。
但是有个很不显然的问题就是这样做的话有一些可行解是让画师去本来就是这个颜色的地方画,假设对于一个位置(i),(a_i=b_i,c_n=a_i),然后并没有其他待染的位置的颜色为(a_i),那么其实这个画师可以去(i)号位置画,但是我们漏掉了这种情况。
因此把所有位置都加进(vector)中,优先处理需要染成别的颜色的位置即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<map>
#include<algorithm>
#define mp make_pair
#define pb push_back
#define N 200005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T,n,m,a[N],b[N],c[N],ans[N];
vector<int>Mp[N];
map<int,int>mpp;
vector<pair<int,int> >G,H;
int main()
{
//freopen("C.in","r",stdin);
//freopen("C.txt","w",stdout);
T=read();
while(T--)
{
n=read();m=read();G.clear();H.clear();mpp.clear();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)b[i]=read(),mpp[b[i]]=i;
for(int i=1;i<=n;i++)Mp[i].clear();
for(int i=1;i<=m;i++)c[i]=read(),Mp[c[i]].pb(i),ans[i]=0;
for(int i=1;i<=n;i++)
{
if(a[i]!=b[i])G.pb(mp(b[i],i));
else H.pb(mp(b[i],i));
}
int siz=G.size(),ff=1;
int sizz=H.size();
for(int i=0;i<sizz;i++)G.pb(H[i]);
siz=G.size();
for(int i=0;i<siz;i++)
{
int x=G[i].first,ii=G[i].second;
if(!Mp[x].size()&&a[ii]!=b[ii])
{
ff=0;
puts("No");
break;
}
if(!Mp[x].size()&&a[ii]==b[ii])continue;
ans[Mp[x][Mp[x].size()-1]]=G[i].second;
Mp[x].pop_back();
}
if(!ff)continue;
int lst=-1;
for(int i=m;i>=1;i--)
{
if(ans[i])
{
lst=ans[i];
}
if(!ans[i]&&lst==-1)
{
ff=0;
puts("No");
break;
}
ans[i]=lst;
}
if(!ff)continue;
puts("Yes");
for(int i=1;i<=m;i++)
{
printf("%d ",ans[i]);
}
puts("");
}
}
CF1481D AB Graph
题意:一个(n)个点的完全图,每条边有一个字符(a)或(b),问是否有一种长为(m)步的走法使得走过的字符串为回文串。
阴间大构造题,其实考场上想到了可以拿三个点乱搞,但是没想到对(mod space 4)的情况分类讨论。
首先考虑两种比较显然的情况:
这里设(w(i,j))表示((i,j))对应的字母
1、在两个位置(i,j)之间有(w(i,j)=w(j,i)),反复横跳即可。
2、(m)为奇数,那么随便找两个点反复横跳即可。
那么最麻烦的问题就是在于(m)为偶数且不符合条件1的情况。
我们考虑有这样的三个点(图来自官方题解)
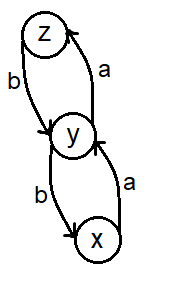
当(m\%4=2)时我们可以选择(x o y o z o y o z o x..... o y o z),构造出形如(aabbaabb...aa)的串
当(m\%4=0)时可以选择(y o z o y o x o y.... o x o y)构造出形如(abbaabba)的串
这里(a,b)究竟是什么没有影响,互换依然成立,于是只要找一下这样的三元组即可,可以提前预处理一下达到(O(n^2))
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int T,n,m,has[N][2];
char ch[N][N];
void solve()
{
memset(has,0,sizeof(has));
n=read();m=read();
for(int i=1;i<=n;i++)scanf("%s",(ch[i]+1));
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j)continue;
has[i][ch[i][j]-'a']=j;
}
}
if(m%2)
{
puts("Yes");
for(int i=1;i<=m+1;i++)
{
if(i%2)printf("2 ");
else printf("1 ");
}
puts("");
return;
}
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
if(ch[i][j]==ch[j][i])
{
puts("Yes");
for(int k=1;k<=m+1;k++)
{
if(k%2)printf("%d ",i);
else printf("%d ",j);
}
puts("");
return;
}
}
}
//cout<<"!!!!!!!!!!!!!
";
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j)continue;
if(!has[j][ch[i][j]-'a'])continue;
int nxt=has[j][ch[i][j]-'a'];
puts("Yes");
if(m%4==2)
{
for(int k=0;k<=m;k++)
{
if(k%4==0)printf("%d ",i);
else if(k%4==1||k%4==3)printf("%d ",j);
else printf("%d ",nxt);
}
}
else
{
for(int k=0;k<=m;k++)
{
if(k%4==0||k%4==2)printf("%d ",j);
else if(k%4==3)printf("%d ",i);
else printf("%d ",nxt);
}
}
return;
}
}
puts("No");
}
int main()
{
T=read();
while(T--)solve();
return 0;
}
CF1481E Sorting Books
题意:(n)本书放在一个书架上,每次可以移动一本到最右边,每本书有一个颜色,你要让所有颜色一致的书挨着,问最少动几本书。
离谱的(dp)题。
移动的很难考虑,那换个角度考虑一下最大化不移动的书的数量。
设(f[i])表示(i-n)这些书中最大的不移动的数量。
考虑(i)这个地方的书是否要动,首先动的话就比较简单,就是(f[i]=f[i+1])。不动的话,那么就是让所有颜色为(a[i])的书都不动,然后动其他的书。
在这里有一个小问题卡了很久就是,设(R[x])表示颜色为(x)的书的最右边的那一个的位置,(L[x])为最左边的,那么我们计算(a[i]=x)的位置(i)的时候要把它右边的书也当作移动处理,这究竟是为什么呢,是因为当(i eq L[a[i]])时这个(f[i])计算的并不是严格的定义上的那个值,而是要考虑前边的书过来的时候的贡献,具体来说就是,你把([i,R[a[i]]])中所有颜色不是(a[i])的书都拿到了后边,但是由于(i eq L[a[i]]),因此前边还有颜色为(a[i])的书,他们也是要拿过来的,拿过来就会放到最右边,因此如果最优方案最终是(i)这本书成为了所有颜色为(a[i])中的书中的第一本,那么最优方案一定是先把(i)前边所有颜色为(a[i])的书都拿到最右边,然后把中间所有的书都拿到右边,在这个过程中即使有些书最开始是在(R[a[i]])右边的,但不过因为右边又来了新的颜色为(a[i])的书,因此还是要再移动过去,因此总移动数是右边所有颜色不是(a[i])的书的数量。
还有一种转移就是:当(i=L[a[i]])时,因为这是这个颜色的书的第一本,因此无需考虑前边再来书的情况,直接把([i,R[a[i]]])间的书全都挪走就好,此时有一种转移方式是(f[i]=count(a[i])+f[R[a[i]]+1]),(count(a[i]))表示颜色为(a[i])的书一共有多少本。
代码很短,但是要好好理解并不简单。
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 500005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,a[N],l[N],r[N],cf[N],f[N];
int main()
{
n=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<=n;i++)if(!l[a[i]])l[a[i]]=i;
for(int i=n;i>=1;i--)if(!r[a[i]])r[a[i]]=i;
for(int i=n;i>=1;i--)
{
cf[a[i]]++;
f[i]=f[i+1];
if(i==l[a[i]])f[i]=max(f[i],cf[a[i]]+f[r[a[i]]+1]);
else f[i]=max(f[i],cf[a[i]]);
}
printf("%d
",n-f[1]);
return 0;
}
CF1481F AB Tree
题意:一棵(n)个节点(1)为根的树,你要给每个节点安排一个字母(a)或(b),使得从根出发,到每个节点的字符串都加入一个集合,要让这个集合的大小最小。并使得有(x)个(a)和(n-x)个字母(b)。输出方案。
大缝合怪题。
首先有一个并不显然的结论是:设树高为(d),答案一定是(d)或(d+1)。
首先答案至少为(d),因为树高为(d)意味着我们一定会有(1-d)中每一个长度的字符串,这就已经(d)个了,因此答案不可能小于(d)。
如果答案为(d),那么就意味着同层的节点(在这里把距离根深度相同的点叫做同层的点)的字符必须相同,设第(i)层的点有(a_i)个,那问题就是从(a)中找一个权值大小为(x)的子集,好像有比较正确的(O(n sqrt n))做法,但是我不会,因此直接随机化把数加入或踢出集合,跑(5000000)次也就比较正确了。
那为什么不是(d)就一定是(d+1)呢,因为我们一定可以构造出一个答案为(d+1)的解。。。
那我们考虑这个解最终长成什么样子:一定是其他所有层,层内的点对应字符都相等,有一层的点中所有的有儿子的点都对应相等。
设(num_{i,0/1})表示(i)层节点无/有儿子的点的个数,(sum_i)表示层数(geq i)的点的个数,很显然(sum)是个后缀和的形式。
假设我们要在(i)层及以下安排(x)个点为(a),其中(xin[0,sum_i]),我们考虑用归纳法构造一组解(也就是说我们默认下一层可以构造出符合条件的解)。
大力讨论一下:
当(xleq sum_{i+1})时,直接把这一层的点都安排为(b),在下一层里搞即可。
当(xgeq sum_i-sum_{i+1})时,直接把这一层点都安排为(a),在下一层里搞即可。
当(sum_{i+1}leq xleq sum_i-sum_{i+1})时,那么注意到左边一定是大于等于(num_{i,1})的,因为每一个有儿子的点至少对应一个儿子,因此(num_{i,1}leq xleq sum_i-sum_{i+1}),那我们直接选(x)个第(i)层的点即可。
这样构造出来的一定符合题意,因为符合我们上述的要求。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<cstdlib>
#include<ctime>
#define pb push_back
#define N 200005
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
int n,na,nb,fa[N],dep[N],f[N][2],num[N][2],sum[N],maxdep;
vector<int>G[N];
vector<int>vec[2][N];
char ans[N];
struct node
{
int id,val;
}a[N];
void dfs(int x)
{
int siz=G[x].size();
dep[x]=dep[fa[x]]+1;
maxdep=max(maxdep,dep[x]);
for(int i=0;i<siz;i++)dfs(G[x][i]);
}
int solve1(int P)
{
int S=0,pos=0,T=5000000;
for(int i=0;i<maxdep;i++)
{
a[i].id=i+1;
a[i].val=num[i+1][0]+num[i+1][1];
}
srand(2039);
while(T--)
{
//cout<<T<<endl;
if(S==P)break;
//cout<<"!!!!!!!!!"<<endl;
if(S<P)
{
int p=rand()%(maxdep-pos)+pos;
S+=a[p].val;swap(a[p],a[pos]);pos++;
//cout<<p<<" "<<pos<<" "<<S<<" "<<P<<endl;
}
else
{
int p=rand()%pos;
S-=a[p].val;--pos;swap(a[pos],a[p]);
//cout<<p<<" "<<pos<<" "<<S<<" "<<P<<endl;
}
}
if(S==P)
{
//cout<<pos<<endl;
for(int i=0;i<maxdep;i++)
{
//cout<<a[i].id<<" "<<a[i].val<<endl;
if(i<pos)f[a[i].id][0]=a[i].val;
else f[a[i].id][1]=a[i].val;
}
return 1;
}
return 0;
}
void solve2(int d,int res,char c0,char c1)
{
int now=num[d][0]+num[d][1];
//cout<<"wolaila!"<<endl;
if(d==maxdep)
{
//cout<<"si!"<<endl;
f[d][c0-'a']=res;
f[d][c1-'a']=now-res;
return;
}
if(res<=sum[d+1])
{
//cout<<"yi!"<<" "<<d<<endl;
solve2(d+1,res,c0,c1);
f[d][c0-'a']=0;f[d][c1-'a']=now;
}
else if(res>=num[d][1]&&res<=now)
{
//cout<<"er!"<<" "<<d<<endl;
solve2(d+1,0,c0,c1);
f[d][c0-'a']=res;f[d][c1-'a']=now-res;
}
else
{
//cout<<"san!"<<" "<<d<<endl;
solve2(d+1,sum[d]-res,c1,c0);
f[d][c0-'a']=now;f[d][c1-'a']=0;
}
}
int main()
{
n=read();na=read();nb=n-na;
if(n==1)
{
puts("1");
if(na==1)puts("a");
else puts("b");
return 0;
}
for(int i=2;i<=n;i++)
{
fa[i]=read();
G[fa[i]].pb(i);
}
dep[1]=1;dfs(1);
for(int i=1;i<=n;i++)
{
vec[(G[i].size()!=0)][dep[i]].pb(i);
if(G[i].size())num[dep[i]][1]++;
else num[dep[i]][0]++;
sum[dep[i]]++;
}
for(int i=maxdep;i>=1;i--)sum[i]+=sum[i+1];
//cout<<solve1(na)<<endl;
//cout<<"!!!!!!!!!"<<endl;
if(!solve1(na))solve2(1,na,'a','b'),printf("%d
",maxdep+1);
else printf("%d
",maxdep);
for(int i=1;i<=maxdep;i++)
{
//printf("%d %d
",f[i][0],f[i][1]);
if(f[i][0]>=num[i][1])
{
for(int j=0;j<vec[1][i].size();j++)ans[vec[1][i][j]]='a';
for(int j=0;j<vec[0][i].size();j++)
{
if(num[i][1]+j<f[i][0])ans[vec[0][i][j]]='a';
else ans[vec[0][i][j]]='b';
}
}
else
{
for(int j=0;j<vec[1][i].size();j++)ans[vec[1][i][j]]='b';
for(int j=0;j<vec[0][i].size();j++)
{
if(num[i][1]+j<f[i][1])ans[vec[0][i][j]]='b';
else ans[vec[0][i][j]]='a';
}
}
}
for(int i=1;i<=n;i++)putchar(ans[i]);
puts("");
}
/*
10 8
8 1 7 10 4 10 4 1 9
15 3
1 15 10 6 15 9 7 11 5 2 7 11 1 2
*/
UPD1:添加了题意