来吧,下个星期软考了,来整合一下必考知识点吧。
1.线性表:将具有“一对一”关系的数据“线性”地存储到物理空间中,这种存储结构就称为线性存储结构(简称线性表)
线性表存储结构:可细分为顺序存储结构(简称顺序表)和链式存储结构(简称链表)
顺序表(顺序存储结构):顺序表存储数据时,会提前申请一整块足够大小的物理空间,然后将数据依次存储起来,存储时做到数据元素之间不留一丝缝隙。我们可以发现,顺序表存储数据同数组非常接近。其实,顺序表存储数据使用的就是数组。
链表(线性存储结构),别名链式存储结构或单链表,用于存储逻辑关系为 "一对一" 的数据。与顺序表不同,链表不限制数据的物理存储状态,换句话说,使用链表存储的数据元素,其物理存储位置是随机的。
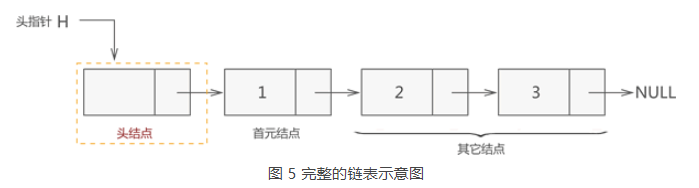
一个完整的链表需要由以下几部分构成:
1.头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
2.节点:链表中的节点又细分为头节点、首元节点和其他节点:
头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题,不可以被删除;
首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
其他节点:链表中其他的节点;
2.树:
1.满二叉树:除最后一层外,每一层上的所有节点都有二个子节点,满二叉树中每一层上的节点的数都达到最大,深度为m的满二叉树有2m-1个节点。
2.完全二叉树:除最后一层外,每一层上的节点数均达到最大值;在最后一层只缺少右边若干个节点,或者左右都没有。
3.平衡二叉树:
4.单支二叉树:
5:二叉排序树:
满二叉树 和 完全二叉树 的区别:
满二叉树必须是除最后一层的节点没有子节点之外,其他层的节点必须要有2个子节点,就是满的状态。
完全二叉树是倒数第二层的节点,只可以没有右子节点或者左右子节点都没有,但是如果没有左子节点(有右子节点)就不是完全二叉树了。
即:满二叉树一定是完全二叉树。但是完全二叉树不一定是满二叉树。
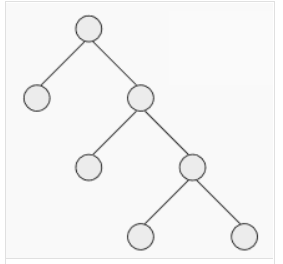
满二叉树:

但是这种就不是满二叉树了。(国外算,国内不算)
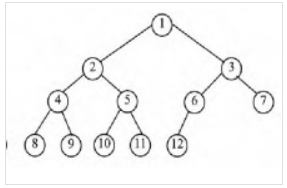
完全二叉树:
计算:
二叉树算叶子节点的个数,一颗度为2的树,有0个度为1的节点,有3个度为2的节点,问叶子节点有多少个?
那么(0*1)是度为1的节点个数 +(3*2)度为2的节点个数 = 6个。再加上一个根节点。即总数有7个,7个再减去3个度为2的节点=4个度为0的节点,即是叶子节点
叶子节点的个数的算法公式:n0 = sum-(n1+n2+1)
3.哈夫曼编码:
主要目的是根据使用频率来最大化节省字符(编码)的存储空间。
简易的理解就是,假如我有A,B,C,D,E五个字符,出现的频率(即权值)分别为5,4,3,2,1,那么我们第一步先取两个最小权值作为左右子树构造一个新树,即取1,2构成新树,其结点为1+2=3,如图:
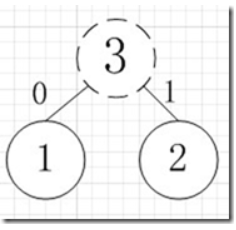
虚线为新生成的结点,第二步再把新生成的权值为3的结点放到剩下的集合中,所以集合变成{5,4,3,3},再根据第二步,取最小的两个权值构成新树,如图:
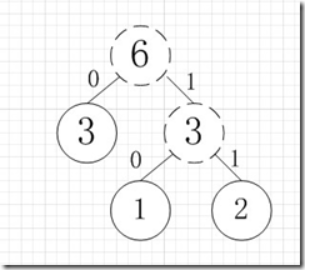
再依次建立哈夫曼树,如下图:
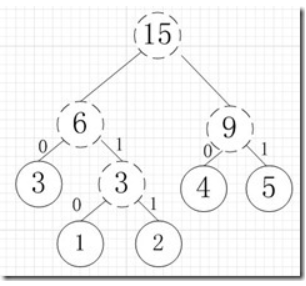
其中各个权值替换对应的字符即为下图:
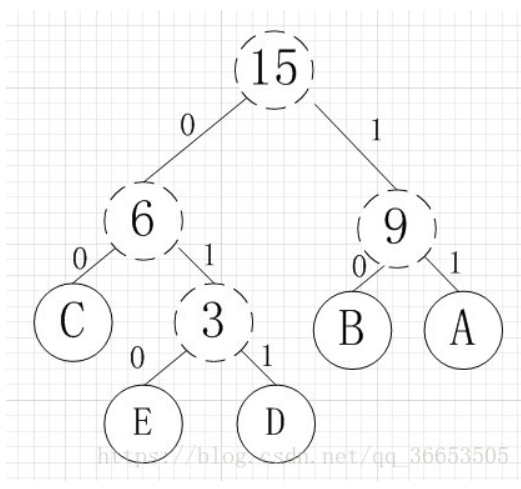
所以各字符对应的编码为:A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。
如果考虑到进一步节省存储空间,就应该将出现概率大(占比多)的字符用尽量少的0-1进行编码,也就是更靠近根(节点少),这也就是最优二叉树-哈夫曼树。
哈夫曼编码 属于前缀编码,根据前缀编码的定义,任一字符的编码都不是另一个字符编码的前缀。
例如:110,100,101,11,1
1就是属于其他字符编码的前缀。
================================================
二。程序语言:
1:程序设计语言分为:
(1)命令式程序设计语言: