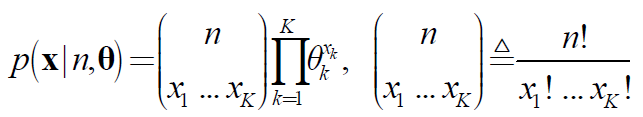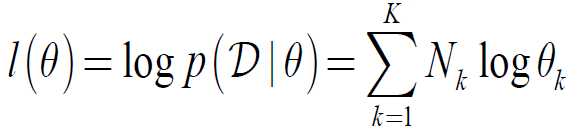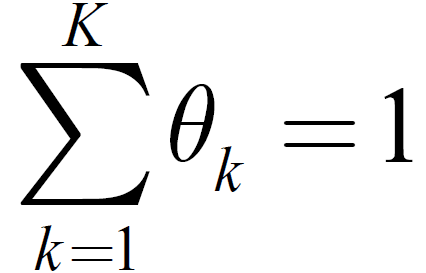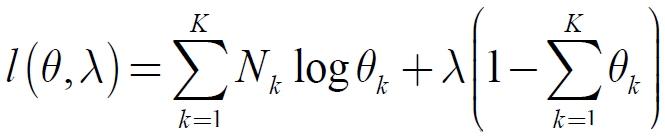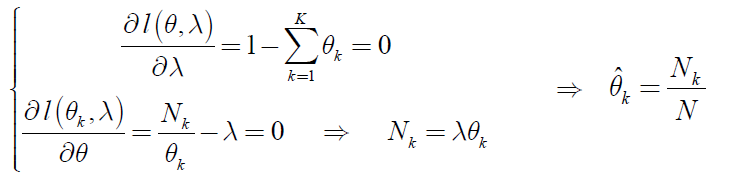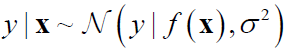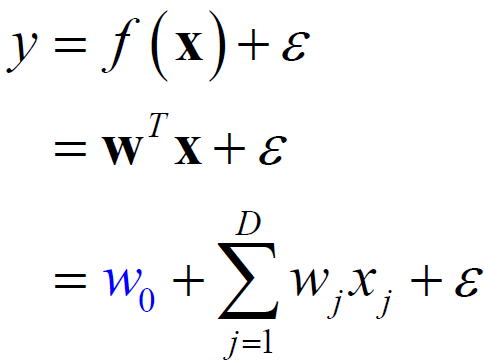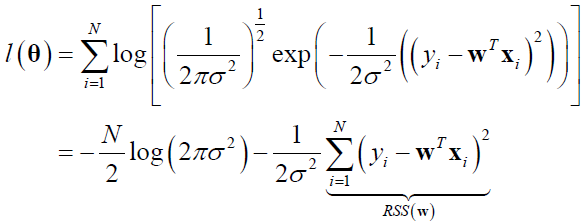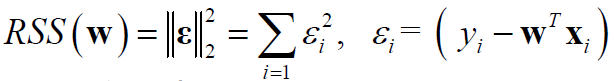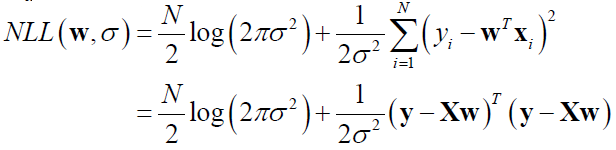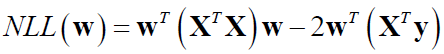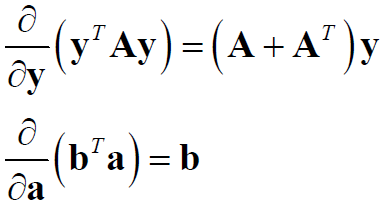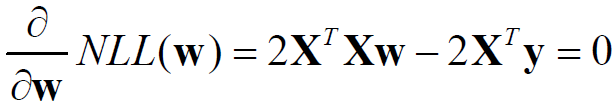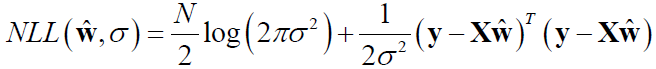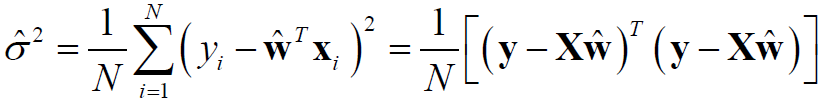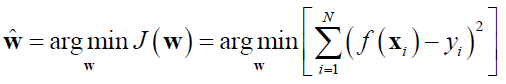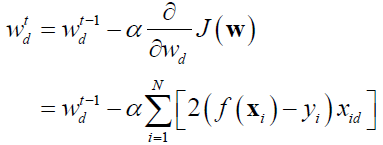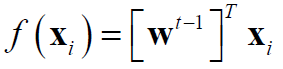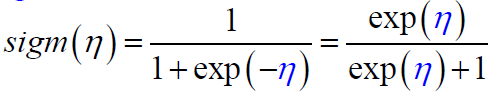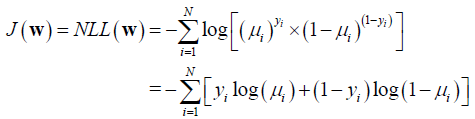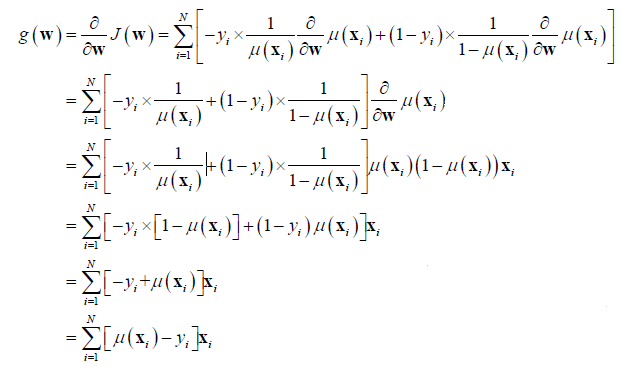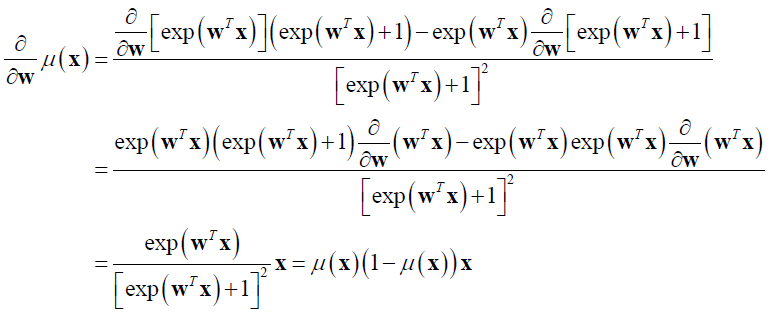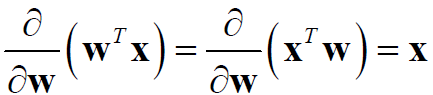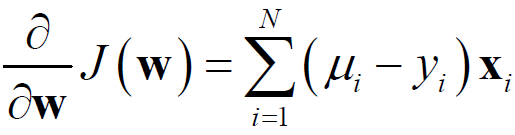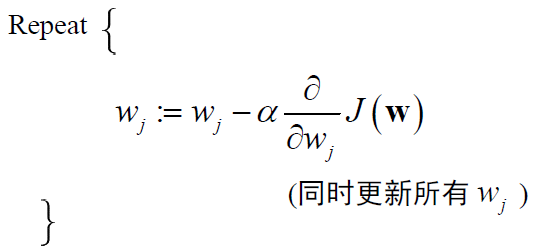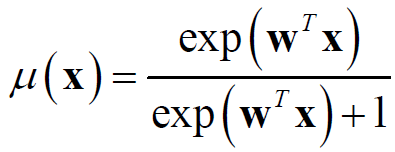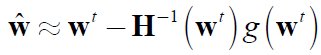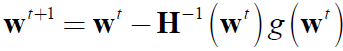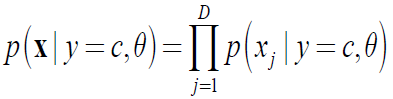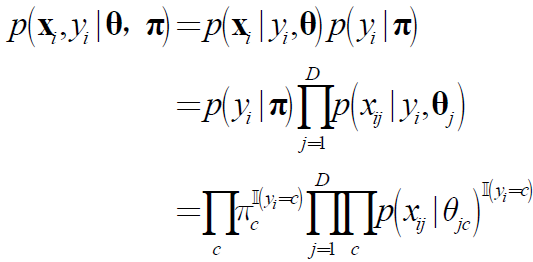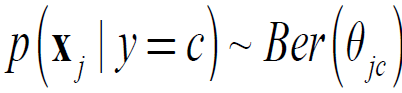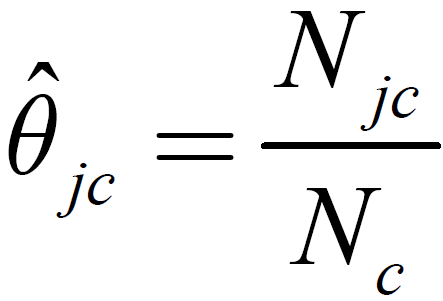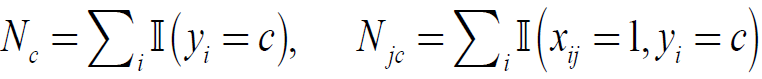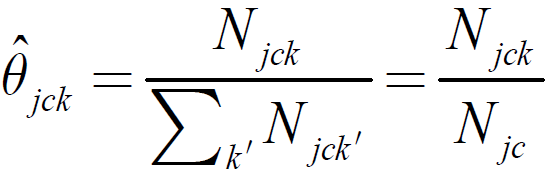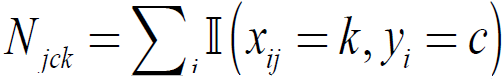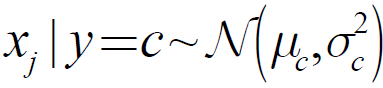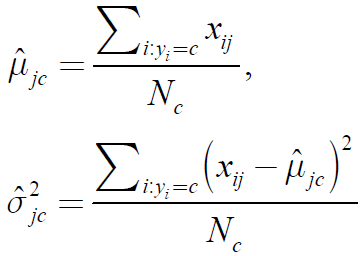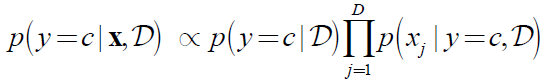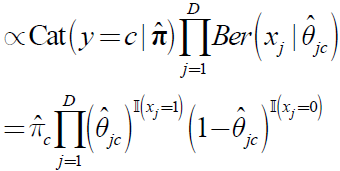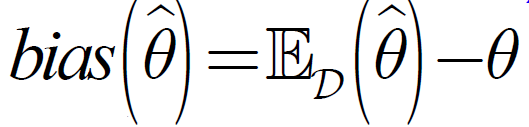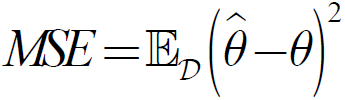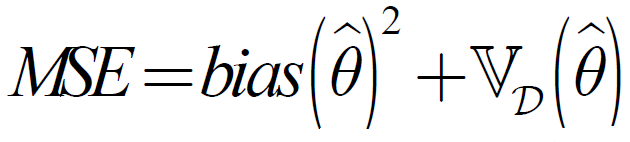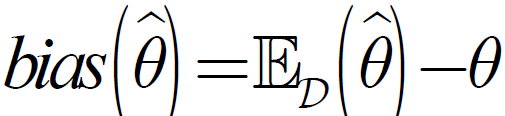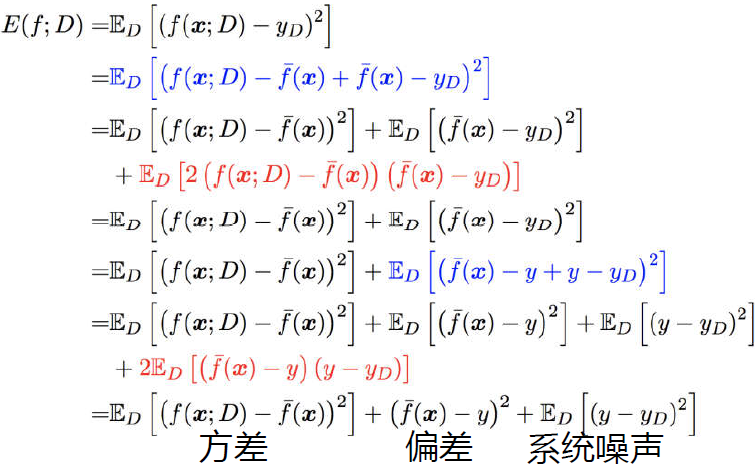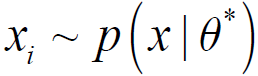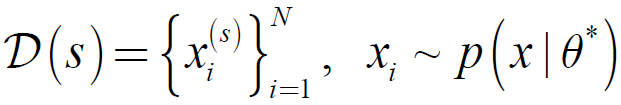目录
4. 朴素贝叶斯(Naive Bayes Classifier, NBC)
一、参数估计
参数估计,即估计模型的参数:给定模型p(x|Ɵ)和数据D,选择与数据最匹配的参数Ɵ。
常用估计模型参数的方法:
(1)矩方法,比如一阶矩,二阶矩,…,K阶矩;
(2)极大释然估计:频率学派
(3)贝叶斯估计:贝叶斯学派
二、极大释然估计
1.似然函数
似然(likelihood,可能性的意思),描述的是事件发生可能性的大小。
似然函数的定义:
设数据D=X1,…,XN为独立同分布(IID),其概率密度函数(pdf)为p(x|Ɵ),则似然函数定义为:
即为在给定数据D的情况下,参数为Ɵ的函数。
2.极大似然估计(MLE)
定义:使得似然函数L(Ɵ)最大的Ɵ的估计:
3.log似然函数
定义:
即:
性质:
(1) 它和似然函数在相同的位置取极大值
(2) 在不引起混淆的情况下,有时记log似然函数为似然函数
(3) 相差常数倍也不影响似然函数取极大值的位置,因此似然函数中的常数项也可以抛弃
(4) 在分类中log似然有时亦称为交叉熵(cross-entropy)
4.损失函数
损失函数 = 负log似然函数,即:
损失函数 = - log p( Ɵ|D)
5.求极大似然估计的一般步骤
(1)选择模型
(2)得到密度函数p(x)
(3)求似然函数L = Ʃ log.p(x)
(4)对似然函数求极值(求导),得到参数估计
三、常见分布的参数估计
1.高斯分布
假设X1,…,XN ~ N (μ, δ2 ),参数为μ, δ2,则高斯分布:
的似然函数为:
其中,
样本均值:
样本方差:
因为有:
高斯分布的似然函数化简为:
求最大值(求梯度,解方程):
得到极值点(一阶导数为0):
说明,使用样本的均值和方差作为高斯分布的参数估计,是极大似然的。
2.Bernoulli分布
Bernoulli分布的密度函数为:
其似然函数为:
其中,N1为试验结果为1的次数,N2为试验结果为0的次数,
求极大似然有:
即样本实验结果为1的比率,是Bernoulli分布的参数Ɵ的极大释然估计。
3.二项分布(Binomia)
Binomia分布的密度函数为:
其似然函数为:
其极大释然估计和Bernoulli分布一样:
求极大似然有:
即样本实验结果为1的比率,是 Binomia分布的参数Ɵ的极大释然估计。
4.多项分布(Multinoull)
Multinoull分布的密度函数为:
其似然函数为(其中NK表示N次试验中出现k的次数):
约束条件为:
采用拉格朗日乘子法求极值:
分别对λ和θk求偏导并令其等于0:
即为θ的最大释然参数估计。
四、机器学习模型的参数估计
1. 回归
(1) 正态分布可用于回归系统噪声建模
(2) 回归是监督学习问题,是输入到输出的映射的学习。
(3) 回归问题的模型:
假设残差服从正态分布:
因此,回归问题的模型可以记为:
回归即预测其输出:
2.线性回归
线性回归:输入与输出呈线性关系。
相信回归的模型:
即:
其中W0是截距,W为权重向量,ε为预测值和真值之间的残差。模型的参数为Ɵ =(W, δ2)
2.1 线性回归的极大似然估计
2.1.1 线性回归的似然函数
线性回归的似然函数为:
其中,RSS表示残差平方和(residual sum of squares),即残差向量的L2模:
注:平均平方误差(MSE) = RSS/N
2.1.2 负log似然函数求参数估计
极大似然等价为极小负log似然损失(negative log likelihood,NLL):
只取与w有关的项,得到:
因为有矩阵求导:
所以NLL求导有:
求解得到:
即为W的极大似然估计,把其代入NLL,则有:
求导有:
求解得:
以上便是线性回归参数Ɵ =(W, δ2)的极大似然估计。
2.1.3 计算机求解线性回归的解极大似然估计
1)当样本数目N较小时,可采用OLS结论,用矩阵QR分解分解得到优化解。
2)当样本数目N较大时,可采用随机梯度下降方法优化求解:
<1> 目标函数:
<2> 梯度下降法步骤:
i)给定初值w0
ii) 更新w,使得J(W)越来越小
iii) w的各维同时更新:
iv) 直到收敛到某个w值,使得J(W)最小
其中,α称为学习率,控制下降速度的大小。
3.Logistic回归
(1)Logistic回归是线性回归的扩展,用于分类任务(0, 1)
(2)分类目标为二值变量,因此服从Bernoulli分布:
其中y为类别输入(0,1)。
假设输入为x的线性组合,即输入为x的函数μ(x),则Bernoulli分布的密度函数可以写为:
其中:0≤μ(x)≤1
(3) 在Logistic回归中,输入的x的函数(概率密度函数)为:
其中sigm()为sigmoid函数,或logistic函数:
(4) logistic回归的概率密度函数为:
3.1 Logistic回归的极大似然估计
(1)负log似然函数求参数估计
Logistic回归的似然函数为:
其中,
μi = μ(xi) = sigm(wTx)
yi = 分类标签(0,1)
(1) 梯度下降法求解
1)对似然函数进行求导
其中,
以上用到的矩阵求导:
2)得到梯度函数
3)使用梯度进行迭代
即:
其中,
(2) 牛顿法求解
1)牛顿法也叫牛顿-拉夫逊(Newton-Raphson)方法,也叫二阶梯度下降法。
2)原理:使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根
3)步骤:
i) 将导数g(w)在wt处进行Taylor展开:
ii) 由上式得到:
iii) 迭代式为:
4. 朴素贝叶斯(Naive Bayes Classifier, NBC)
4.1定义
假设共有C个类别y∈(1,2,…,C),每个类别有特征X=(x1,x2,…xD), 则朴素贝叶斯为假设各维特征在给定类别标签的情况下条件独立:
概率密度函数:
其中,π、θ分别为y的先验分布和类条件分布的参数。
4.2朴素贝叶斯的极大似然估计
(1)似然函数为:
其中Nc为y=c的样本数。
则参数估计:
其中:
(4) 如果服从正泰分布
则参数估计:
(5) 使用朴素贝叶斯进行预测
将给定数据条件D换成参数的MLE插入,得到:
例如Bernoulli分布的预测:
五、估计的评价
1. 估计量的评价标准
一个好的估计具有的性质:
(1) 无偏性:估计量的期望等于真值的期望:
即估计的偏差(bias):
等于0。
(2) 相容性
若:
则该估计是相容(consistent)的。
(3) 有效性
无偏估计中,方差较小的一个更有效(收敛速度更快)
2. 偏差-方差分解
点估计的性能通过均方误差(MSE, mean squared error)来评价:
可分解为:
其中,
估计的偏差为:
估计的变化程度(精度)为:
(1) 如果bias = 0, 称其为无偏估计
(2) 为了使估计的MSE小,估计的偏差和方差到要小。
3. 监督学习模型的偏差-方差分解
在回归任务中,学习算法f的平方预测误差期望为:
(1) 偏差:学习算法的预测的期望与真实结果的偏离程度, 即刻画了学习算法本身的拟合能力。
(2) 方差:同样大小的训练集的变动所导致的学习性能的变化, 即刻画了数据扰动所造成的影响。
(3) 噪声:在当前任务上任何学习算法所能达到的期望泛化误差的下界, 即刻画了学习问题本身的 难度。
4. 估计的抽样分布
解决的问题:分布的参数真值未知,无法产生真实的模拟数据。
如何解决?:估计的抽样分布
估计的抽样分布:
假设从真实分布:
中进行S次抽样,每次的样本集的大小均为N, 得到数据集合
根据每次抽样得到的数据D(s),都会得到一个估计:
当S -> ∞ 时,使用估计的参数代替真实的参数,称为估计的抽样分布。
4.1 参数Bootstrap
Bootstrap(一种重采样技术),用![]() 代替
代替![]() ,从分布
,从分布![]() 中产生样本。
中产生样本。
4.2 非参数Bootstrap
从原始数据中进行N次有放回地采样N个数据,用经验分布近似真正的分布
- tany 2017年10月9日于杭州
人工智能从入门到专家教程资料:https://item.taobao.com/item.htm?spm=a1z38n.10677092.0.0.38270209gU11fS&id=562189023765
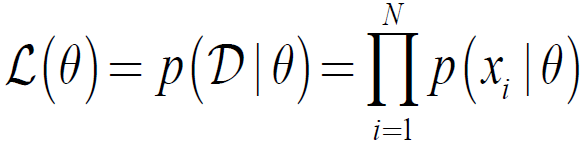
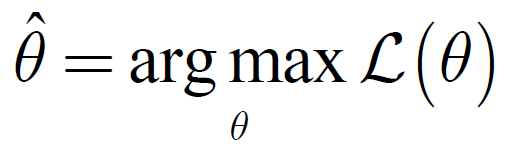
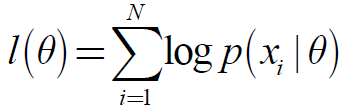
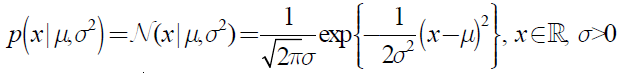
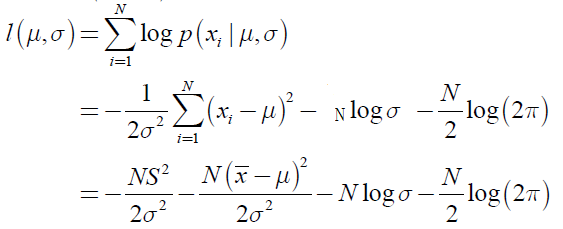
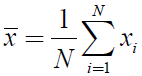
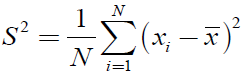
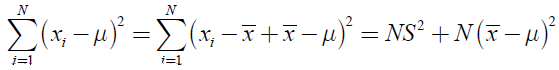
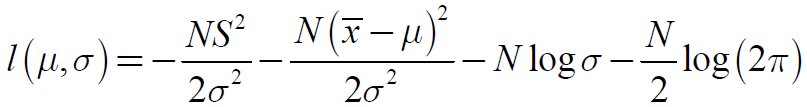
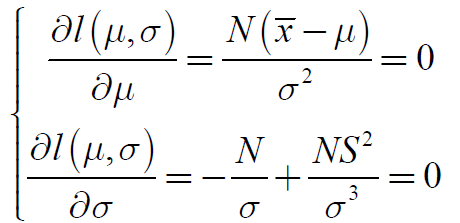
![clip_image012[4] clip_image012[4]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171009214234902-1773362397.png)
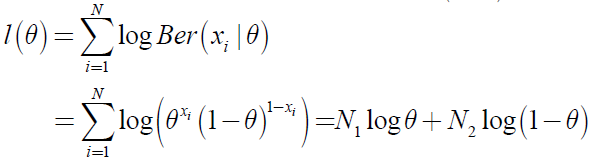

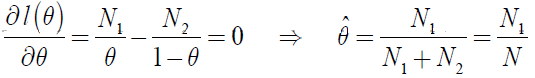
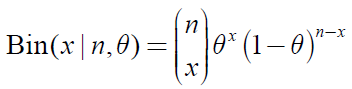
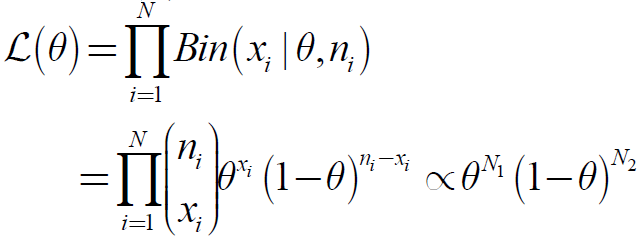
![clip_image016[1] clip_image016[1]](https://images2017.cnblogs.com/blog/718363/201710/718363-20171009214253605-1404196741.png)