画直线算法 Line drawing algorithm

画直线算法 Line drawing algorithm

Line drawing algorithm 罗列了几种在屏幕像素上画直线的算法。

自己想

但我自己想的话可能就会变成这样：

首先问自己几个问题：

Q1： 算法的输入？

两个实数点。

Q2：算法的输出？

若干个自然数点。

Q3：怎么展示算法结果？

屏幕上的像素可以抽象成一个二维数组，点作为坐标索引来定位，给二维数组赋值相当于给像素上色。

然后思考过程：

两个实数点算出来一个实数域上的实数直线方程。但显然此方程的解不能直接作为算法的解，它还需要再通过一个函数过滤成自然数的解。

real_points = line_equation(p1, p2)
natural_points = func(real_points)

最直接的想法是每次迭代，得到实数解之后，我都有两个选择：

1. 选上一个自然数解
2. 选上一个自然数解 + 1

那我选择的标准是什么？是离谁更近。因为我离这两个选择都不会超过 1 ，所以我离谁小于 0.5 ，就选谁。

如下如图所示（注意为了方便画图像素中心点放在了左下角），画出最典型的情况：斜率大于零且两个点满足 x0 < x1, y0 < y1。红点代表实数解，绿点代表上一个自然数解，蓝点代表上一个自然数解 + 1 ，最后选择的像素标记为黄块块。起点随便选一个，每次看蓝点近选蓝点，绿点近选绿点。

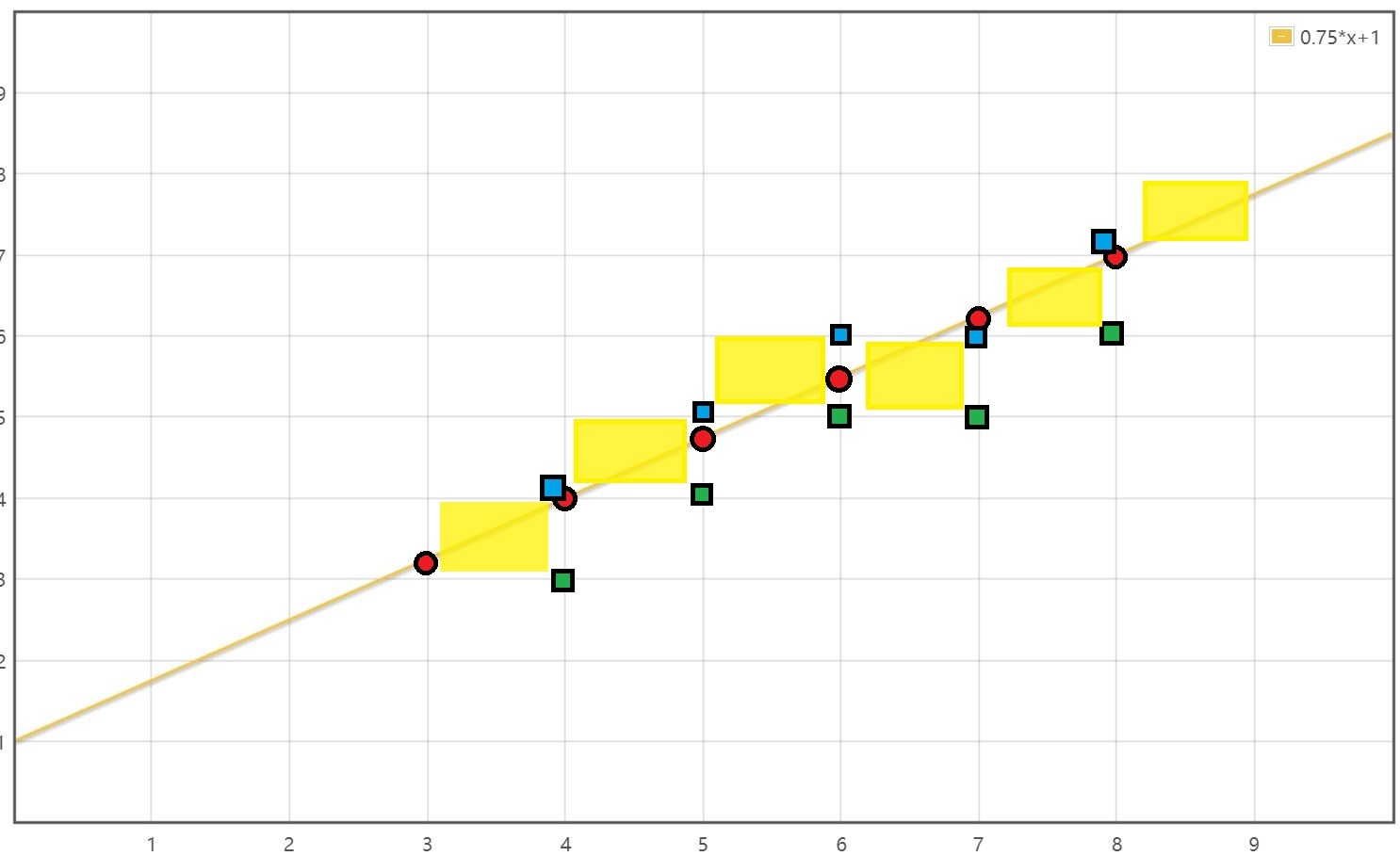
x0 < x1, y0 < y1 

function line(x0, y0, x1, y1) 
    real slope := (y1 - y0 / x1 - x0)
    real realy:= y0
    int y := y0
    for x from x0 to x1 
        plot(x, y)
        realy := realy + slope
        if realy - y ≥ 0.5 then
             y := y + 1

边界和顺序问题就很多了。比如对直线分类讨论：

• 水平的（斜率为零）
• 垂直的（斜率为无穷大）
• 斜的（其他可能的斜率）

还有 x0 > x1 怎么处理等等。

Bresenham's line algorithm

计算的是每一像素点与该线之间的误差。误差应为每一点x中，其相对的像素点之y值与该线实际之y值的差距。每当x的值增加1，误差的值就会增加slope。每当误差的值超出0.5，线就会比较靠近下一个映像点，因此y的值便会加1，且误差减1。

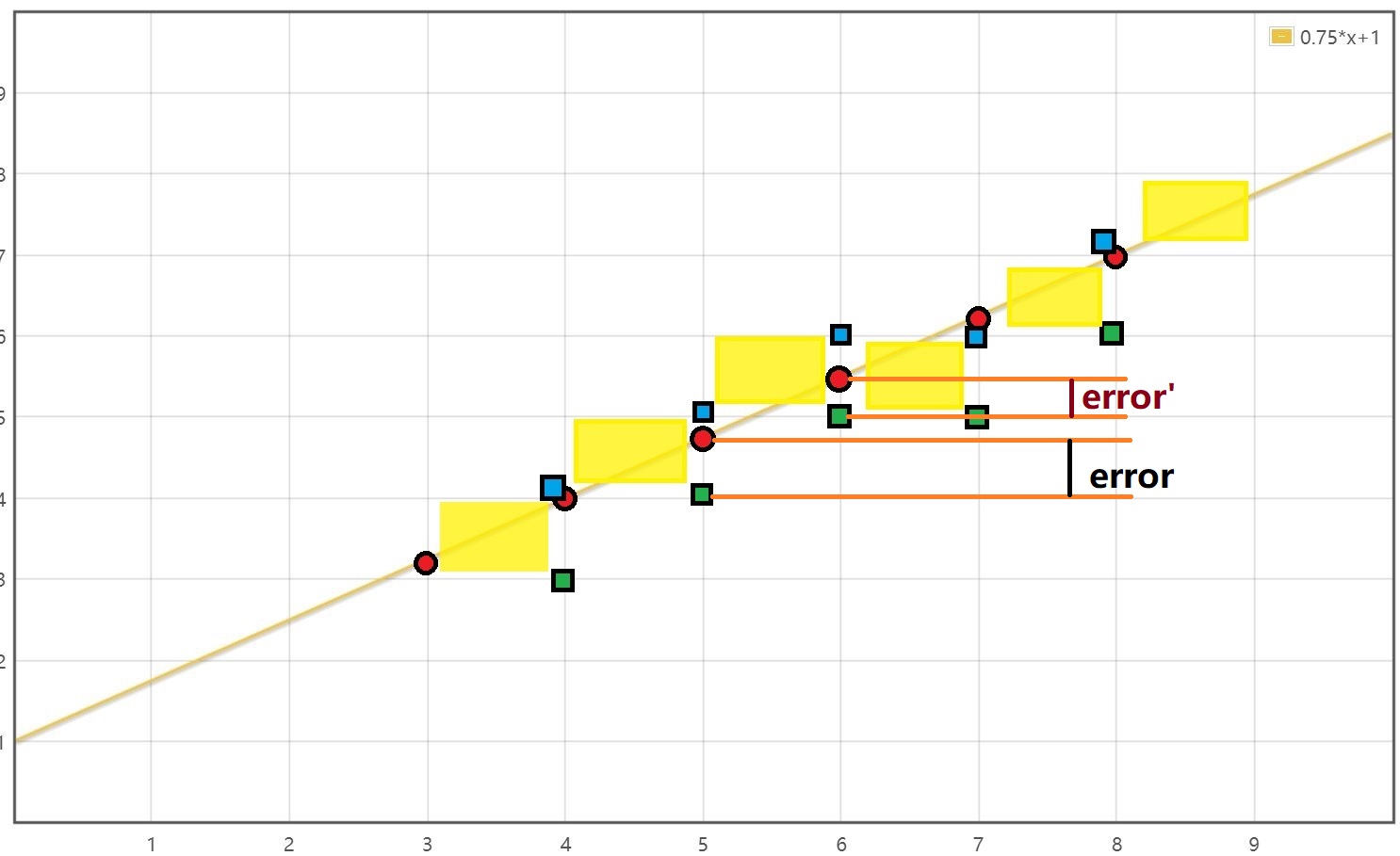
如上图，其实 error 算的就是红点和绿点之间的差距。比如看 x = 5 的时候，假设 error = 0.6 ，要选蓝点，所以 error - 1 = -0.4 。然后下次迭代 error = error + slope = -0.4 + 0.75 = 0.35 。

x0 < x1, y0 < y1 

function line(x0, y0, x1, y1)
    real slope := (y1 - y0 / x1 - x0)
    real error := 0.0 // No error at start
    int y := y0
    for x from x0 to x1 
        plot(x, y)
        error := error + slope
        if error ≥ 0.5 then
            y := y + 1
            error := error - 1.0

【本质上跟我想的差不多】

测试代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int width = 20;
const int height = 20;
const char clear_char = ' ';
const char mark_char = '*';

char screen[width][height];

struct point 
{ 
    int x, y; 
    point(int _x, int _y) : x(_x), y(_y) {}
};

typedef void(*method)(point&, point&);

struct testcase
{
    point p0, p1;
    method func;

    testcase(point _p0, point _p1, method _func) : p0(_p0), p1(_p1), func(_func) {}

    void run() { func(p0, p1); }
};

void draw_pixel(int x, int y)
{
    // 按照数学惯例，我们会认为数组的第一个索引是 y，也就是行数
    screen[y][x] = mark_char;
}

void show_screen()
{
    cout << endl;
    // 同样按照数学惯例，行数需要做一个翻转，这样原点才在左下角
    for (int i = width - 1; i >= 0; --i)
    {
        for (int j = 0; j < height; ++j)
            cout << screen[i][j];
        cout << endl;
    }
    cout << 0;
    for (int i = 0; i < width; ++i) cout << '=';
}


void native(point& p0, point& p1)
{
    memset(screen, clear_char, sizeof(screen));

    // 对边界情况的处理思路：
    // 1. 对直线分类讨论
    // 水平线
    if (p0.y == p1.y)
    {
        int dx = p0.x < p1.x ? 1 : -1;
        for (int x = p0.x; x != p1.x; x += dx)
            draw_pixel(x, p0.y);
    }
    // 垂直线
    else if (p0.x == p1.x)
    {
        int dy = p0.y < p1.y ? 1 : -1;
        for (int y = p0.y; y != p1.y; y += dy)
            draw_pixel(p0.x, y);
    }
    // 斜线
    else
    {
        // 2. 始终迭代 x
        // 3. 必须满足 p0.x <= p1.x, 如果不是则交换
        if (p0.x > p1.x) 
            swap(p0, p1);

        // 4. 那么还有两种情况
        // p0.y <= p1.y 斜率为正
        // p0.y > p1.y 斜率为负
        double slope = static_cast<double>(p1.y - p0.y) / (p1.x - p0.x);
        int dy = p0.y > p1.y ? -1 : 1; 
        float realy = p0.y;
        int y = p0.y;
        for (int x = p0.x; x <= p1.x; ++x)
        {
            draw_pixel(x, y);
            realy += slope;
            if (abs(realy - y) > 0.5)
                y = y + dy;
        }
    }
    show_screen();
}

void bresenham(point& p0, point& p1)
{
    memset(screen, clear_char, sizeof(screen));

    if (p0.y == p1.y)
    {
        int dx = p0.x < p1.x ? 1 : -1;
        for (int x = p0.x; x != p1.x; x += dx)
            draw_pixel(x, p0.y);
    }
    // 垂直线
    else if (p0.x == p1.x)
    {
        int dy = p0.y < p1.y ? 1 : -1;
        for (int y = p0.y; y != p1.y; y += dy)
            draw_pixel(p0.x, y);
    }
    // 斜线
    else
    {
        // 2. 始终迭代 x
        // 3. 必须满足 p0.x <= p1.x, 如果不是则交换
        if (p0.x > p1.x) 
            swap(p0, p1);

        // 4. 那么还有两种情况
        // p0.y <= p1.y 斜率为正
        // p0.y > p1.y 斜率为负
        double slope = static_cast<double>(p1.y - p0.y) / (p1.x - p0.x);
        int dy = p0.y > p1.y ? -1 : 1; 
        float error = 0.0;
        int y = p0.y;
        for (int x = p0.x; x <= p1.x; ++x)
        {
            draw_pixel(x, y);
            error += slope;
            if (abs(error) > 0.5)
            {
                y = y + dy;
                error -= 1.0;
            }
        }
    }
    show_screen();

}

int main()
{
    testcase tcs[] = 
    {
        { point(2, 3), point(2, 10), native },
        { point(11, 5), point(1, 5), native },
        { point(1, 1), point(8, 6), bresenham },
        { point(1, 1), point(8, 6), native },
        { point(3, 1), point(15, 3), bresenham},
        { point(3, 1), point(15, 3), native},
        { point(10, 1), point(1, 17), bresenham},
        { point(10, 1), point(1, 17), native},
    };

    for (testcase& t : tcs) t.run();

    return 0;
}