(纯白话算法系列)插入排序、时间复杂度分析、代码演示

定义

插入排序（Insertion sort）是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序，这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分：第一部分包含了这个数组的所有元素，但将最后一个元素除外（让数组多一个空间才有插入的位置），而第二部分就只包含这一个元素（即待插入元素）。在第一部分排序完成后，再将这个最后元素插入到已排好序的第一部分中。

插入排序的基本思想是：每步将一个待排序的记录，按其关键码值的大小插入前面已经排序的文件中适当位置上，直到全部插入完为止。

纯白话说：其实插入排序就像玩扑克牌一样，一张一张拿牌，第一张牌肯定不需要排序，手上就那么一张牌，再给你一张牌，你就会比较，如果新牌大就放在右边，新牌比第一张手牌小，就把新牌放在左边位置，现在手上只有两张牌，而且是排好序的，再给第三张牌也是一样，先看看是不是比右边的牌大，如果小于右边的话，就交换位置，如果比第一张牌还小，就继续交换位置，目前位置三张牌就都保持从小到大的顺序了，如果再发牌也是这样重复。。。

来看一张动态图

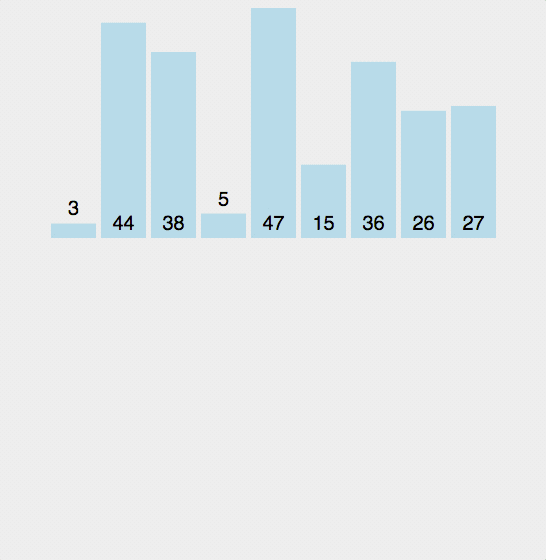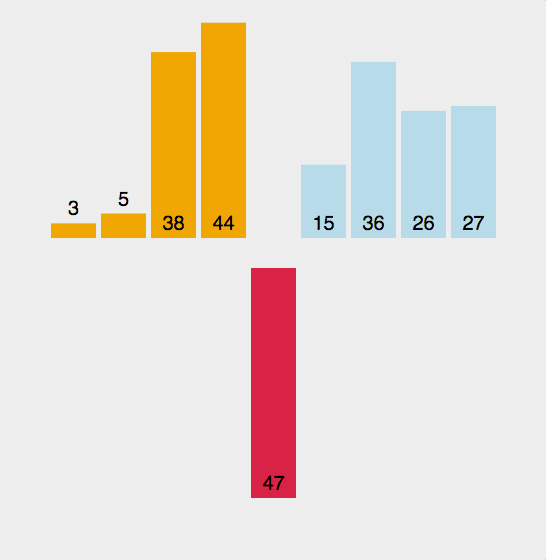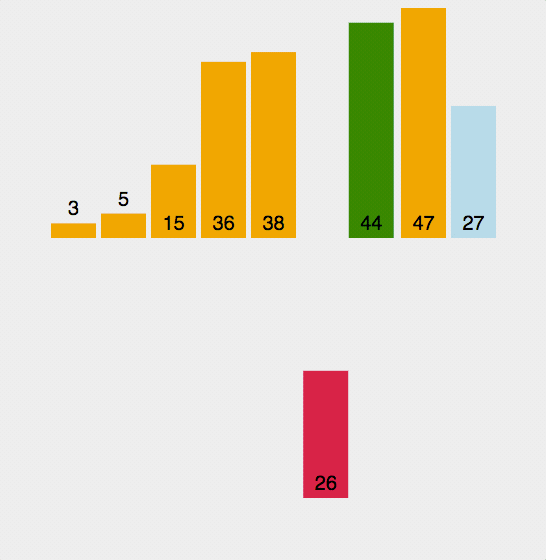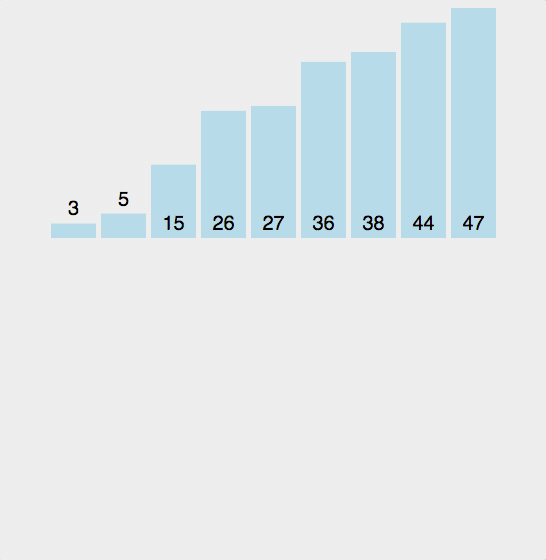
图片摘自–https://www.cnblogs.com/wupeixuan/archive/2018/03/26/8654938.html
只要玩过扑克牌的都应该很容易理解这种排序算法。
我们直接上代码：

package com.bean.insertion_sort;

import java.util.Arrays;

public class InsertionSort {
    public static void insertSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j >= 0 && arr[j] > arr[j+1]; j--)
                swap(arr, j, j+1);
        }
    }

    private static void swap(int[] arr, int left, int right) {
       int temp = arr[left];
       arr[left] = arr[right];
       arr[right] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {2,5,1,8,13,3};
        insertSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

代码解释：

首先还是老样子，如果数组为空或者元素个数少于2，则无排序必要。

然后，想一下你取牌的顺序，是一张一张的拿，而且每次取完牌后都进行排序保证手牌总是排好序的，所以第一层for循环就相当于你拿牌的过程，手牌张数从1开始一张一张递增直到数组的长度为止。第二层for循环表示新拿的牌从右往左依次比较，如果比右边的牌小，就交换位置，直到所有牌的顺序都ok。

举个栗子

拿我代码中的例子来说[2,5,1,8,13,3]，这是所有的待发手牌，先给你一张2，不需要排序，然后给你一张5,5>2，所以放在右边就好了不用更换位置，第三张牌是1，小于5，所以交换位置为2,1,5，1还是小，则继续跟2交换位置，1,2,5，结束本次循环，再发一张牌8，8>5，不用交换，当前顺序为1,2,5,8，又发了一张13,13>8，不用交换位置，当前顺序为1,2,5,8,13，再发一张3,3<13，交换位置，3<8，交换位置，3<5交换位置，3>2，停止移动，最终顺序为：

时间复杂度

很明显，这种排序仍然需要一张一张比较，所以又是一个等差数列，时间复杂度为O(n²)。但是大家想一下，对选择排序来说，就算传进入一个有序数列，是不是还是要每次都完全按照流程来执行？选择总是把最小的元素和当前循环的第一个位置进行交换。但是对于插入排序来说就不是这样了，倘若给你发的牌是1,2，3,4，5，你觉得还需要每次排序到最后一位么？肯定是不需要的，给你一张1，不用排，给一张2，跟1比一下，不用换位置，给一张3，跟2比一下，不用换位置，也不用跟1再比较了，给一张4，同理，不需要跟2,1，比较，也不需要调换位置，给一张5，也一样，不需要跟3,2，1,比大小，更不需要换位置，所以涉及到一种新的说法：最好情况和最坏情况和平均情况。

最差情况：O(n²)
最好情况：O(n)
平均情况：O(n²)

一般是按照最坏的复杂度计算的，所以通常说插入排序的复杂度是O(n²)