在幼儿园的时候,我们就学习过把一个数分成(a)与(b),我们只需要用计算机来模拟这个过程就可以了。
我们先从奇数开始看起,以(5)为例:
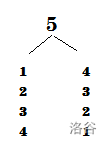
我们可以发现,(5)可以分成(1)和(4),(2)和(3),(3)和(2),以及(4)和(1),也就是说,一个奇数可以有(n-1)种方法进行分解,去重后也就是((n-1)div2)种方法。
可以在举一个例子,如(7),它可以分成(1)和(6),(2)和(5),(3)和(4),(4)和(3),(5)和(2),(6)和(1),去重后就是(1)和(6),(2)和(5),(3)和(4),共(3)种,再用刚刚推出的公式,((7-1) div 2 = 3),发现公式是正确的。
再看偶数,在这里以(4)为例。
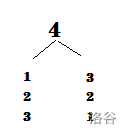
我们可以发现,一共有(3)种方法可以将(4)分解,和奇数一样,也有(n-1)种方案,其中,(2)与(2)是重复的,去掉,(3)和(1)也是重复的,去掉。因此我们发现,(4)只有(1)和(3)一种分解方法,可以用((n-1)div2)的方法判断。
最后我们发现,他们的公式都一样,所以可以直接套公式。
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
cout<<(n-1)/2;
return 0;
}