使用python编程代写进行贝叶斯统计分析

原文链接：http://tecdat.cn/?p=7637

 

本文讲解了使用PyMC3进行基本的贝叶斯统计分析过程. 

# Imports
import pymc3 as pm # python的概率编程包
import numpy.random as npr # numpy是用来做科学计算的
import numpy as np
import matplotlib.pyplot as plt # matplotlib是用来画图的
import matplotlib as mpl

from collections import Counter # ? 
import seaborn as sns # ? 
# import missingno as msno # 用来应对缺失的数据

# Set plotting style
# plt.style.use('fivethirtyeight')
sns.set_style('white')
sns.set_context('poster')

%load_ext autoreload
%autoreload 2
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import warnings
warnings.filterwarnings('ignore')

使用python进行贝叶斯统计分析 

  ​

贝叶斯公式 

 

贝叶斯主义者的思维方式 

根据证据不断更新信念

pymc3 

​

常见的统计分析问题 

• 参数估计: "真实值是否等于X"

• 比较两组实验数据: "实验组是否与对照组不同? "

问题1: 参数估计 

"真实值是否等于X?"

或者说

"给定数据，对于感兴趣的参数，可能值的概率分布是多少？"

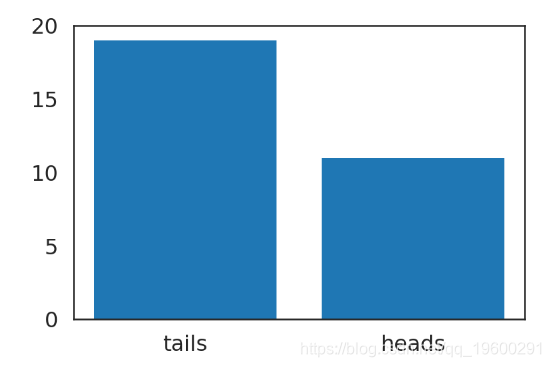
例 1: 抛硬币问题 

我把我的硬币抛了 n次，正面是 h次。 这枚硬币是有偏的吗？

参数估计问题parameterized problem 

先验假设 

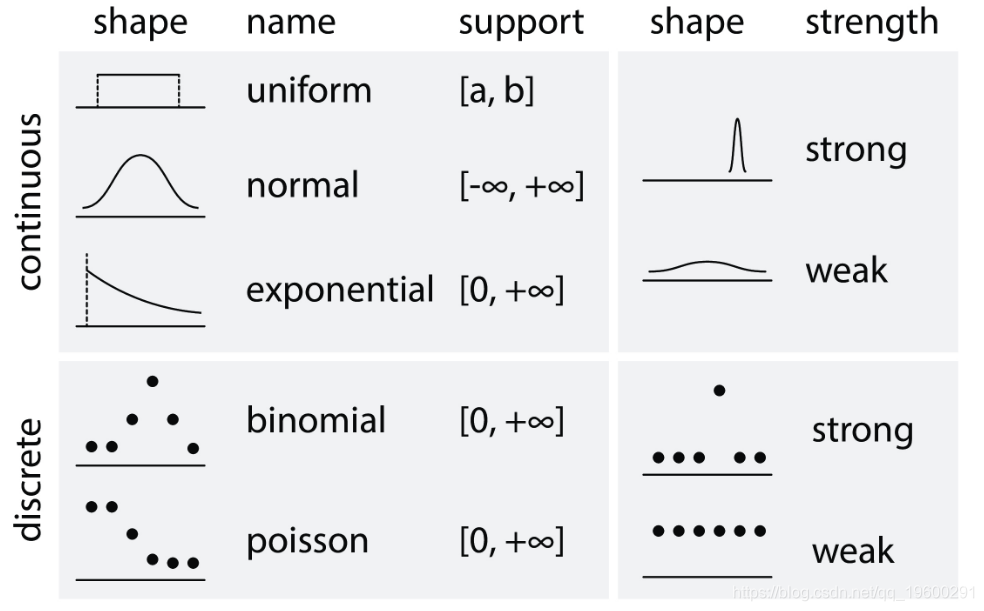
• 对参数预先的假设分布:  p∼Uniform(0,1)
• likelihood function(似然函数, 翻译这词还不如英文原文呢): data∼Bernoulli(p)

# 产生所需要的数据
from random import shuffle
total = 30
n_heads = 11
n_tails = total - n_heads
tosses = [1] * n_heads + [0] * n_tails
shuffle(tosses)

数据 

fig = plot_coins()
plt.show()    

​

MCMC Inference Button (TM) 

100%|██████████| 2500/2500 [00:00<00:00, 3382.23it/s]

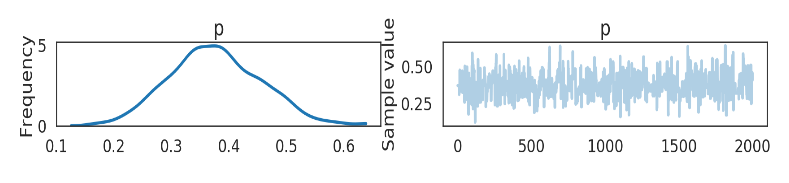
结果 

pm.traceplot(coin_trace)
plt.show()

​

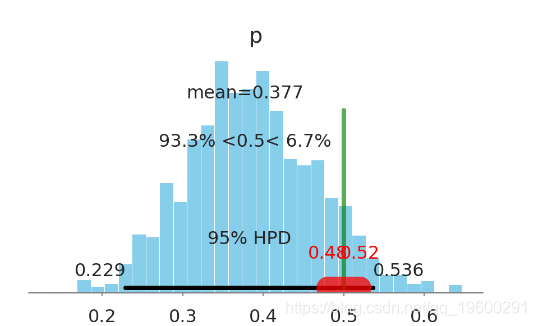
In [10]:

 
plt.show()

​

• 95% highest posterior density (HPD, 大概类似于置信区间) 包含了 region of practical equivalence (ROPE, 实际等同区间).

 

例 2: 药品活性问题 

我有一个新开发的分子X; X在阻止流感病毒复制方面有多好？

实验 

• 测试X的浓度范围, 测量流感活性

• 计算 IC50: 能够抑制病毒复制活性50%的X浓度.

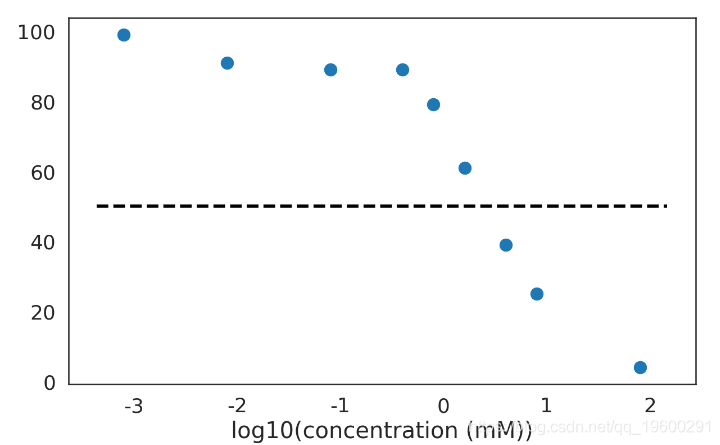
data 

 
import pandas as pd

chem_df = pd.DataFrame(chem_data)
chem_df.columns = ['concentration', 'activity']
chem_df['concentration_log'] = chem_df['concentration'].apply(lambda x:np.log10(x))
# df.set_index('concentration', inplace=True)

参数化问题parameterized problem 

给定数据, 求出化学物质的IC50值是多少, 并且求出置信区间( 原文中the uncertainty surrounding it, 后面看类似置信区间的含义)?

先验知识 

• 由药学知识已知测量函数(measurement function):  m=β1+ex−IC50
• 测量函数中的参数估计, 来自先验知识: β∼HalfNormal(1002)
• 关于感兴趣参数的先验知识: log(IC50)∼ImproperFlat
• likelihood function: data∼N(m,1)

数据 

In [13]:

fig = plot_chemical_data(log=True)
plt.show()

​

MCMC Inference Button (TM) 

In [16]:

pm.traceplot(ic50_trace[2000:], varnames=['IC50_log10', 'IC50'])  # live: sample from step 2000 onwards.
plt.show()

​

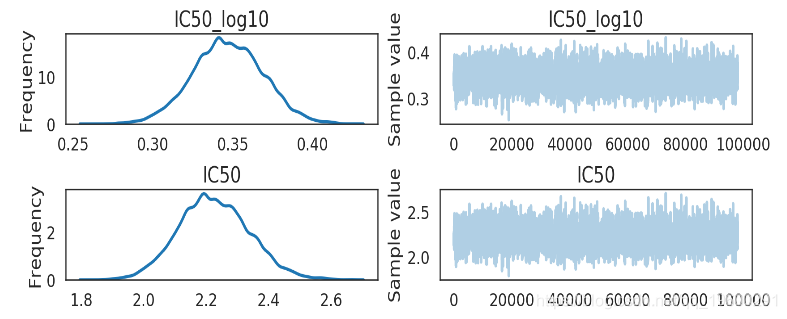
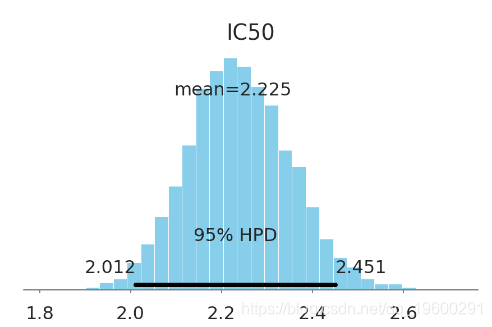
结果 

In [17]:

pm.plot_posterior(ic50_trace[4000:], varnames=['IC50'], 
                  color='#87ceeb', point_estimate='mean')
plt.show()

​

该化学物质的 IC50 大约在[2 mM, 2.4 mM] (95% HPD). 这不是个好的药物候选者. 在这个问提上不确定性影响不大, 看看单位数量级就知道IC50在毫摩的物质没什么用...

第二类问题: 实验组之间的比较 

"实验组和对照组之间是否有差别? "

例 1: 药品对IQ的影响问题 

药品治疗是否影响(提高)IQ分数?

 

def ECDF(data):
    x = np.sort(data)
    y = np.cumsum(x) / np.sum(x)
    
    return x, y

def plot_drug():
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    x_drug, y_drug = ECDF(drug)
    ax.plot(x_drug, y_drug, label='drug, n={0}'.format(len(drug)))
    x_placebo, y_placebo = ECDF(placebo)
    ax.plot(x_placebo, y_placebo, label='placebo, n={0}'.format(len(placebo)))
    ax.legend()
    ax.set_xlabel('IQ Score')
    ax.set_ylabel('Cumulative Frequency')
    ax.hlines(0.5, ax.get_xlim()[0], ax.get_xlim()[1], linestyle='--')
    
    return fig

In [19]:

# Eric Ma自己很好奇, 从频率主义的观点, 差别是否已经是具有"具有统计学意义"

from scipy.stats import ttest_ind

ttest_ind(drug, placebo) # (非配对) t检验. P=0.025, 已经<0.05了

Out[19]:

Ttest_indResult(statistic=2.2806701634329549, pvalue=0.025011500508647616)

实验 

• 参与者被随机分为两组:
  • 给药组 vs. 安慰剂组
• 测量参与者的IQ分数

先验知识 

• 被测数据符合t分布:  data∼StudentsT(μ,σ,ν)

以下为t分布的几个参数:

• 均值符合正态分布:  μ∼N(0,1002)
• 自由度(degrees of freedom)符合指数分布:  ν∼Exp(30)
• 方差是positively-distributed:  σ∼HalfCauchy(1002)

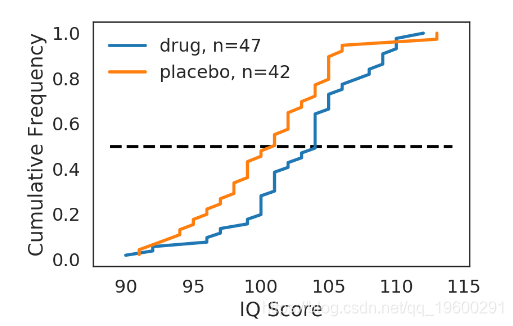
数据 

In [20]:

fig = plot_drug()
plt.show()

​

代码 

In [21]:

y_vals = np.concatenate([drug, placebo])
labels = ['drug'] * len(drug) + ['placebo'] * len(placebo)

data = pd.DataFrame([y_vals, labels]).T
data.columns = ['IQ', 'treatment']

MCMC Inference Button (TM) 

结果 

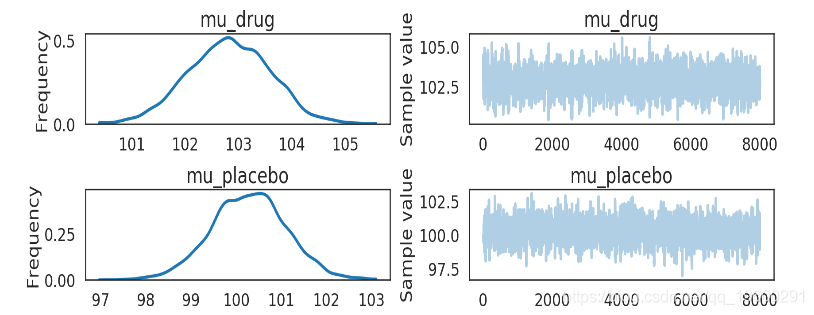
In [24]:

pm.traceplot(kruschke_trace[2000:], 
             varnames=['mu_drug', 'mu_placebo'])
plt.show()

​

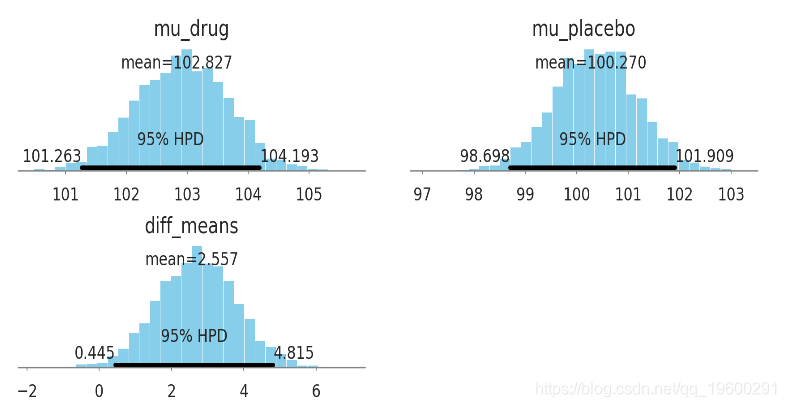
In [25]:

pm.plot_posterior(kruschke_trace[2000:], color='#87ceeb',
            varnames=['mu_drug', 'mu_placebo', 'diff_means'])
plt.show()

​

• IQ均值的差距为: [0.5, 4.6]
• 频率主义的 p-value: 0.02 (!!!!!!!!)

注: IQ的差异在10以上才有点意义. p-value=0.02说明组间有差异, 但没说差异有多大. 这个故事说的是虽然有差异, 但是差异太小了, 也没啥意思.

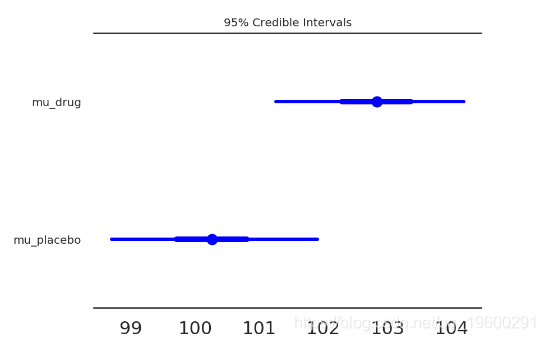
In [27]:

 
ax = adjust_forestplot_for_slides(ax)
plt.show()

​

森林图：在同一轴上的95％HPD（细线），IQR（粗线）和后验分布的中位数（点），使我们能够直接比较治疗组和对照组。

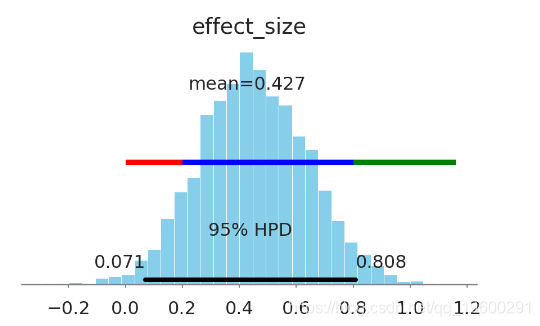
In [29]:

ax = pm.plot_posterior(kruschke_trace[2000:], 
                       varnames=['effect_size'],
                       color='#87ceeb')
overlay_effect_size(ax)

​

• 效果大小（Cohen's d, 效果微小, 效果中等, 效果很大）可以从微小到很大（95％HPD [0.0，0.77]）。
•  这种药很可能是无关紧要的。
• 没有生物学意义的证据。

例 2: 手机消毒问题  

比较两种常用的消毒方法, 和我的fancy方法, 哪种消毒方法更好

实验设计 

• 将手机随机分到6组: 4 "fancy" 方法 + 2 "control" 方法.
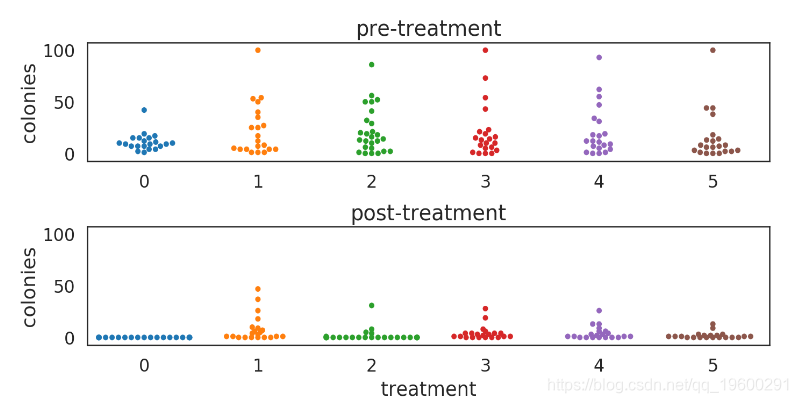
• 处理前后对手机表面进行拭子菌培养
• count 菌落数量, 比较处理前后的菌落计数

Out[30]:

sample_id                 int32
treatment                 int32
colonies_pre              int32
colonies_post             int32
morphologies_pre          int32
morphologies_post         int32
year                    float32
month                   float32
day                     float32
perc_reduction morph    float32
site                      int32
phone ID                float32
no case                 float32
frac_change_colonies    float64
dtype: object

数据 

In [32]:

fig = plot_colonies_data()
plt.show()

​

先验知识 

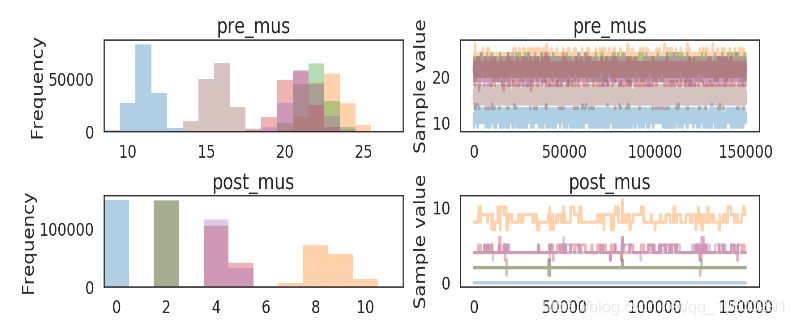
菌落计数符合泊松Poisson分布. 因此...

• 菌落计数符合泊松分布:  dataij∼Poisson(μij),j∈[pre,post],i∈[1,2,3...]
• 泊松分布的参数是离散均匀分布:  μij∼DiscreteUniform(0,104),j∈[pre,post],i∈[1,2,3...]
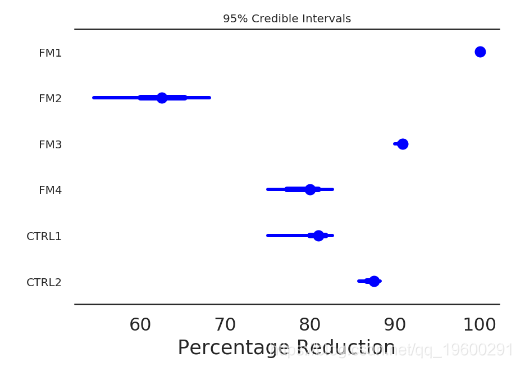
• 灭菌效力通过百分比变化测量，定义如下:  mupre−mupostmupre

MCMC Inference Button (TM) 

In [34]:

with poisson_estimation:
    poisson_trace = pm.sample(200000)

Assigned Metropolis to pre_mus
Assigned Metropolis to post_mus
100%|██████████| 200500/200500 [01:15<00:00, 2671.98it/s]

In [35]:

pm.traceplot(poisson_trace[50000:], varnames=['pre_mus', 'post_mus'])
plt.show()

​

结果 

In [39]:

pm.forestplot(poisson_trace[50000:], varnames=['perc_change'], 
              ylabels=treatment_order) #, xrange=[0, 110])
plt.xlabel('Percentage Reduction')

ax = plt.gca()
ax = adjust_forestplot_for_slides(ax)

​

 

 

 

如果您有任何疑问，请在下面发表评论。