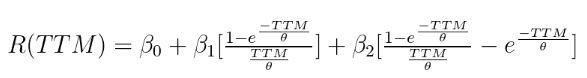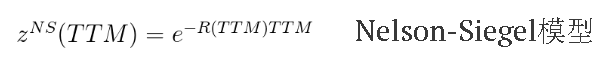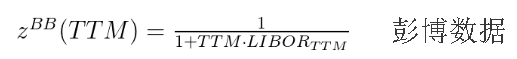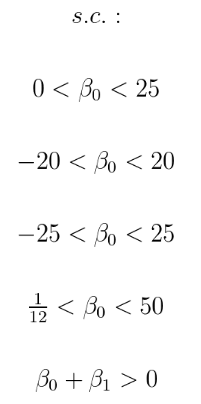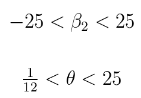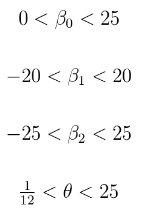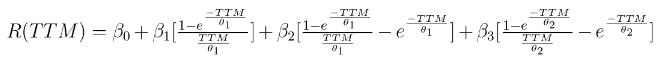原文链接:http://tecdat.cn/?p=11680
这篇文章的目的是指导读者逐步使用R编程语言实现Nelson-Siegel模型的步骤。您可能已经知道,估计利率期限结构是任何资产定价的关键,因此对投资者和政策制定者起着重要的作用。想法是使一条连续曲线适合现有数据。就是说,给定可获取的利率和相应的到期日(通过彭博社或任何其他数据提供商),可以使用Nelson-Siegel方法得出利率的期限结构。
-
R或RStudio
-
LIBOR / OIS利率和相应的到期日(通过彭博社或其他数据提供商)
一点理论…
在开始执行模型之前,让我们回顾一下基础知识。
Nelson-Siegel零息债券的到期收益率:
零息债券价格:
优化问题:
这个想法是两个价格应该相等。因此,我们想找到使两个价格之间的平方差平方和最小的Nelson-Siegel因素。
实施模型的步骤
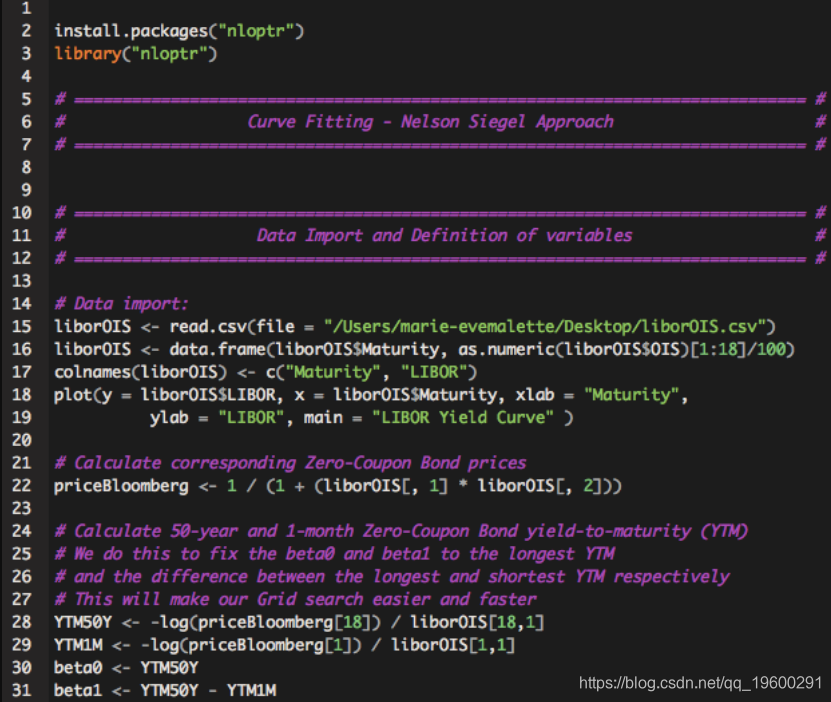
第1步:数据导入和变量定义
- 我们导入LIBOR / OIS利率和相应的到期日,对其进行过滤,然后将其存储在数据框中。
- 然后,我们使用导入的LIBOR / OIS汇率计算每个到期日的零息票价格。
- 我们最终计算出最长(50年)和最短(1个月)到期的到期收益率(YTM)。
- 为了简化步骤2中描述的网格搜索和步骤3中描述的优化问题,我们将近似
- 为了简化步骤2中描述的网格搜索和步骤3中描述的优化问题,我们将近似
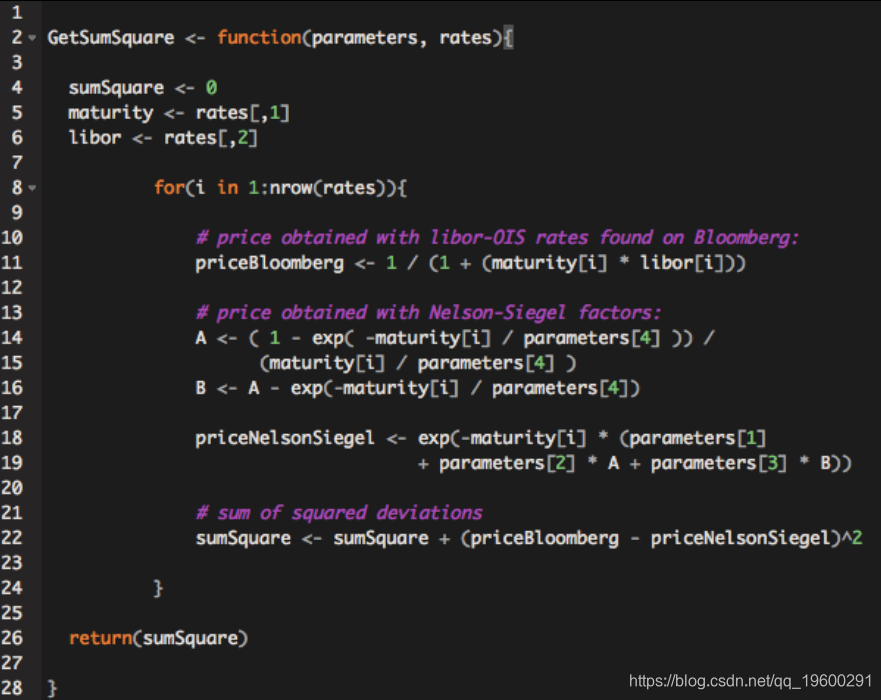
步骤2:对目标函数进行编程
- 我们对函数进行编程,该函数计算LIBOR / OIS利率给出的零息债券价格与Nelson-Siegel模型给出的零息债券价格之间的平方偏差的平方和。
步骤3:网格搜索
- 我们定义为我们的参数范围 :
- 我们创建一个包含所有可能的组合矩阵 。
- 我们选择产生最小平方偏差总和的组合作为我们的初始参数,以插入优化问题。
步骤4:优化问题
- ,我们可以解决非线性优化问题:
- 初始参数(x0)是在网格搜索中找到的参数。
- 目标函数(eval_f)是在步骤2中编程的目标函数。
- 上限和下限(ub和lb)定义如下:
步骤5:调整模型
此时获得完美契合的机会非常渺茫。必须重复步骤3和4调整模型。进一步来说:
- 我们必须围绕步骤5中获得的结果执行第二次网格搜索,搜索范围较窄,然后重新运行优化问题。
- 您可能还想尝试使用不同的参数组合,得出平方偏差的第二,第三或第四最小和。
- 我们也将要执行的最后一个网格搜索 在第二轮优化得到的数值。
- 技巧 –在模型中尝试不同的初始参数时,针对LIBOR / OIS Bloomberg数据点绘制通过求解参数获得的最终收益曲线,以了解其拟合程度。没有完美的方法可以完成–这是一个反复试验的过程。
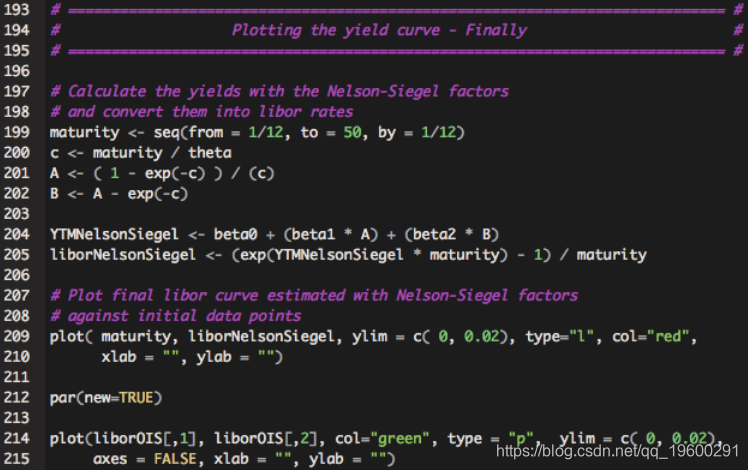
步骤6:绘制估计的收益曲线
现在,我们有了Nelson-Siegel因子,可以估算出收益率曲线:
结果与结论
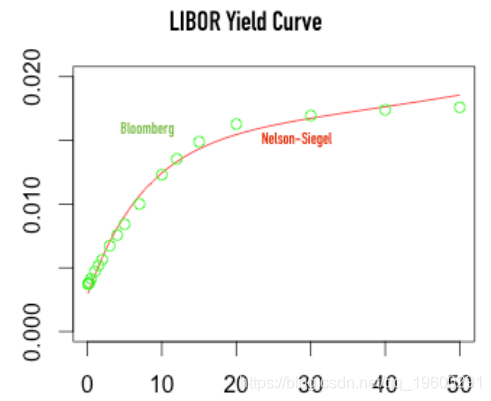
下图以红色显示了所获得的LIBOR收益率曲线。彭博LIBOR / OIS汇率以绿色显示。
尽管曲线可以很好地拟合数据点,但是我们可以看到拟合并不完美。Nelson-Siegel模型的替代方案是Svensson模型,该模型增加了两个参数以实现更好的拟合。
Svensson模型–零票息收益率:
实施Svensson模型的步骤与实施Nelson-Siegel模型的步骤相同。