R语言分位数回归、GAM样条曲线、指数平滑和SARIMA对电力负荷时间序列预测

原文链接：http://tecdat.cn/?p=18359 

电力负荷预测是电网规划的基础，其水平的高低将直接影响电网规划质量的优劣。为了准确预测电力负荷，有必要进行建模。本文在R语言中使用分位数回归、GAM样条曲线、指数平滑和SARIMA模型对电力负荷时间序列预测并比较。

用电量

本文使用的数据是1996年至2010年之间的每周用电量数据，序列

1.  
    
2.  
   load ("Load.RData")
3.  
   plot (ts( data = Load , start= 1996 , frequency = 52) )

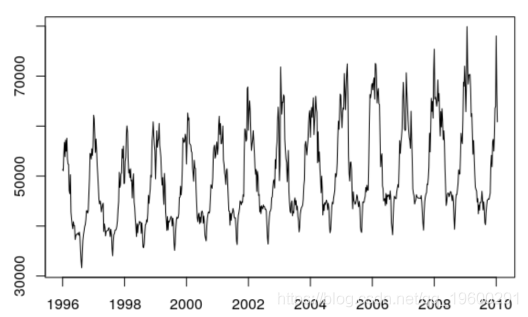
用电量变量及其影响因素：
•星期几（离散）
•时间小时（离散或非参数）
•年（连续）

交互影响：
•日期和时间

•年份和时间

活动
•公共假期

温度对模型的影响：高温、低温和极冷温度
 

模型：
分段线性函数，
GAM模型中的样条曲线
 

数据探索

时间对电力负荷的影响

> plot ( NumWeek , Load )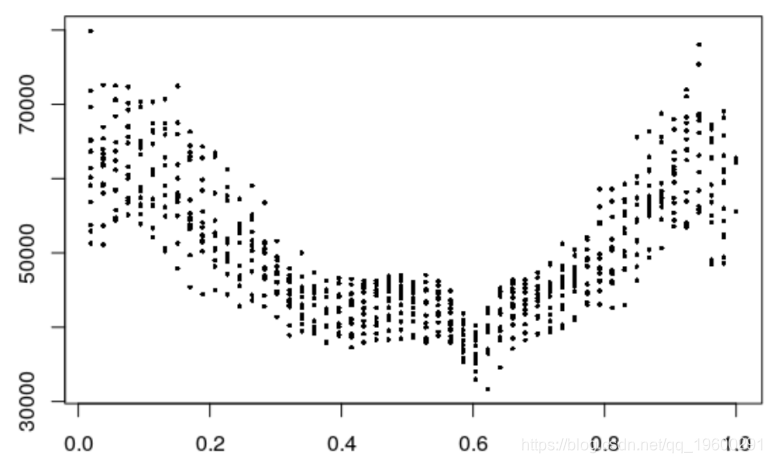

温度对电力负荷的影响，（Tt，Yt）

> plot ( Temp , Load )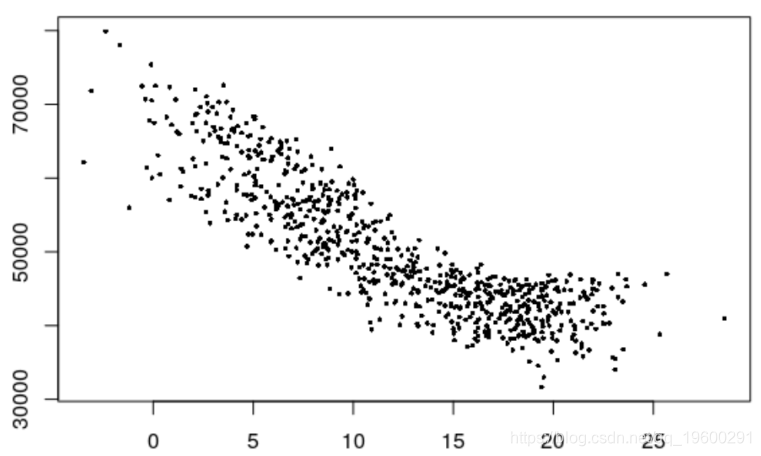

负荷序列（Yt）的自相关的影响，

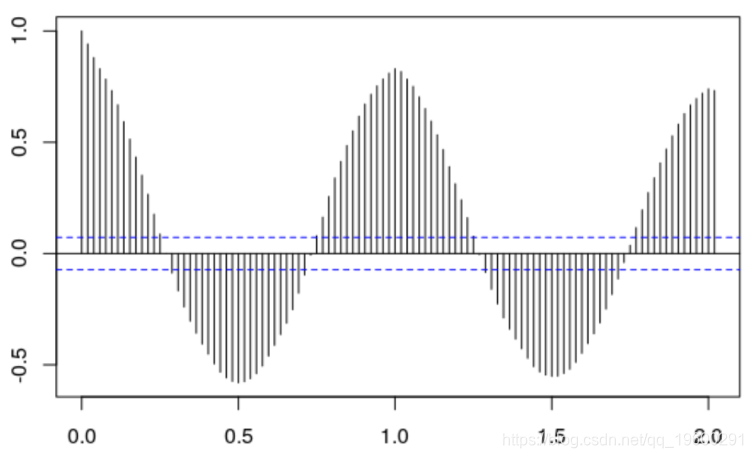
> acf (Load )

 

OLS与 中位数回归
 

中位数回归通过单调变换是稳定的。

1.  
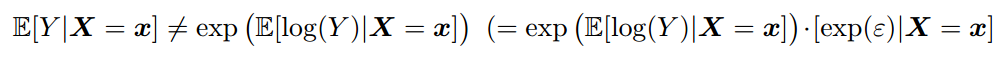
   lm(y˜x, data =df)
2.  
   lm(y˜x, data =df , tau =.5)

现在，中位数回归将始终有两个观察结果。

1.  
    
2.  
   which ( predict ( fit ))
3.  
   21 46

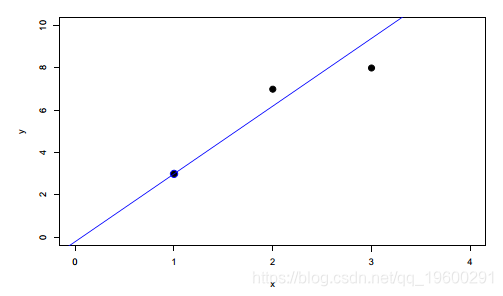
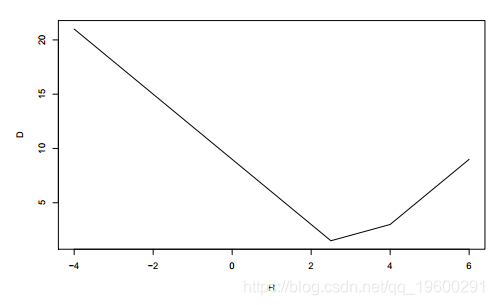
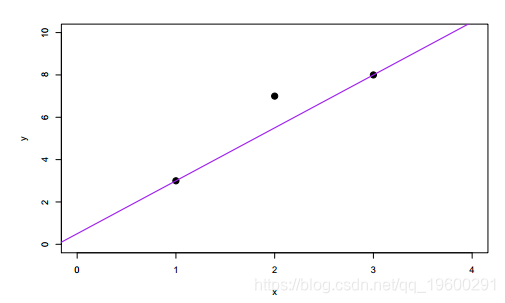
分位数回归和指数平滑

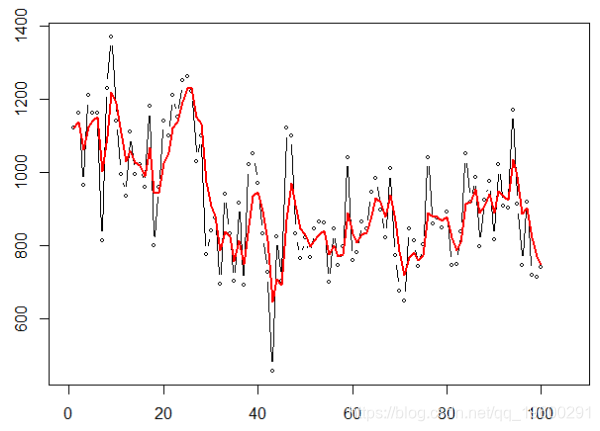
简单的指数平滑：

经典地，我们寻找使预测误差最小的α，即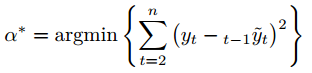

1.  
    
2.  
   X=as. numeric ( Nile )
3.  
   SimpleSmooth = function (a){
4.  
    
5.  
   for (t in 2:T{L[t=a*X[t+(1 -a)*L[t -1
6.  
    
7.  
   }lines ( SimpleSmooth (.2) ,col =" red ")
8.  
    

1.  
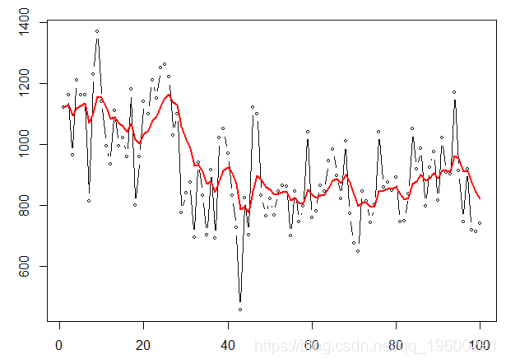
   V= function (a){
2.  
    
3.  
   for (t in 2:T){
4.  
   L[t]=a*X[t]+(1 -a)*L[t -1]
5.  
   erreur [t]=X[t]-L[t -1] }
6.  
   return ( sum ( erreur ˆ2) )
7.  
    
8.  
   optim (.5 ,V)$ par
9.  
   [1] 0.2464844
10.  
    hw= HoltWinters (X, beta =FALSE
11.  
    hw$ alpha
12.  
    [1] 0.2465579

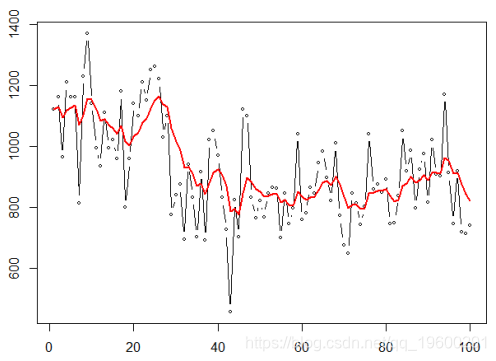
我们可以考虑分位数误差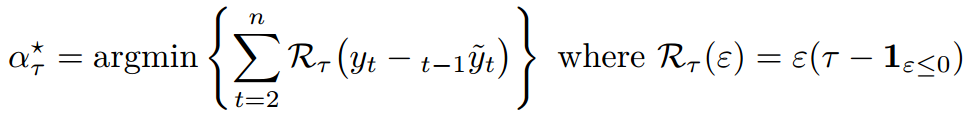

1.  
   HWtau = function ( tau ){
2.  
   loss = function (e) e*(tau -(e< ;=0) *1)
3.  
   V= function (a){
4.  
    
5.  
    
6.  
   for (t in 2:T){
7.  
   L[t]=a*X[t+(1 -a)*L[t -1
8.  
   erreur [t=X[t-L[t -1
9.  
   return ( sum ( loss ( erreur
10.  
     
11.  
    optim (.5 ,V)$ par
12.  
     

1.  
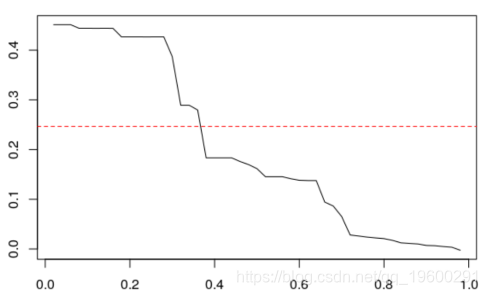
   plot (X, type ="b",cex =.6
2.  
    
3.  
   lines ( SimpleSmooth ( HWtau (.8,col=" blue ",
4.  
   lwd =2)

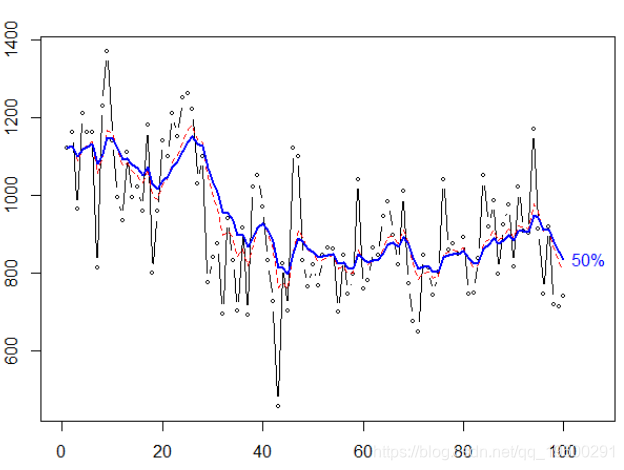
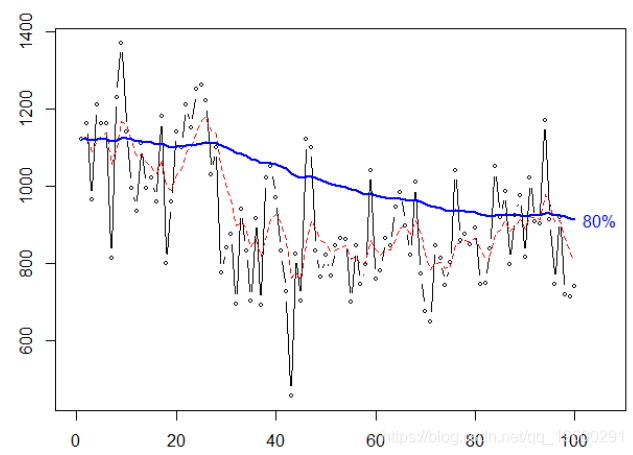
双指数平滑

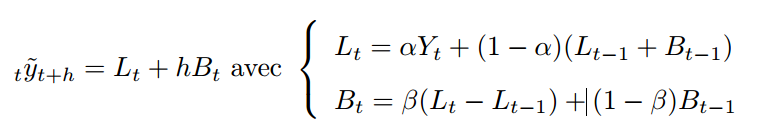
我们考虑分位数误差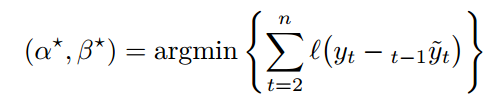

其中。

1.  
    
2.  
   hw= HoltWinters (X, gamma =FALSE ,l. start =X[1])
3.  
   hw$ alpha
4.  
   alpha
5.  
   0.4223241
6.  
   hw$ beta
7.  
   beta
8.  
   0.05233389
9.  
    
10.  
    DouSmo = function (a,b){
11.  
     
12.  
    for (t in 2:T){
13.  
    L[t]=a*X[t+(1 -a*(L[t -1]+ B[t -1]
14.  
    B[t]=b*(L[t]-L[t -1]) +(1 -b*B[t -1]
15.  
    return (L+B)

 

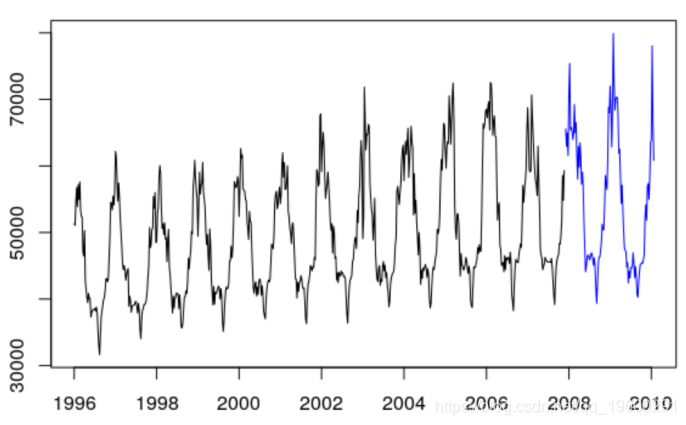
预测

数理统计建立在对概率模型参数的估计和假设检验的基础上。
统计中的预测：当模型拟合观测值时，它会提供良好的预测。
相反，我们使用没有出现过的场景，它使我们能够评估未来的主要趋势，而不是预测极端事件的能力。

 

预测变量的构造
 

1.  
    
2.  
   plot (ts( data = Load $Load , start =
3.  
   1996 , frequency = 52) ,col =" white "

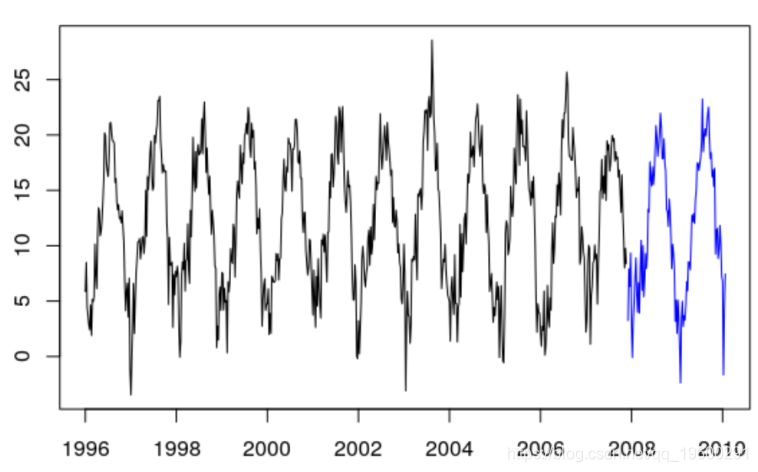
回归

1.  
   plot (ts( data = Temp , start =
2.  
   1996 , frequency = 52) ,
3.  
   lines (ts( data = train $Temp , start =
4.  
   1996 , frequency = 52) )
5.  
   lines (ts( data = test $Temp , start =
6.  
   1996+620 /52, frequency = 52)

 

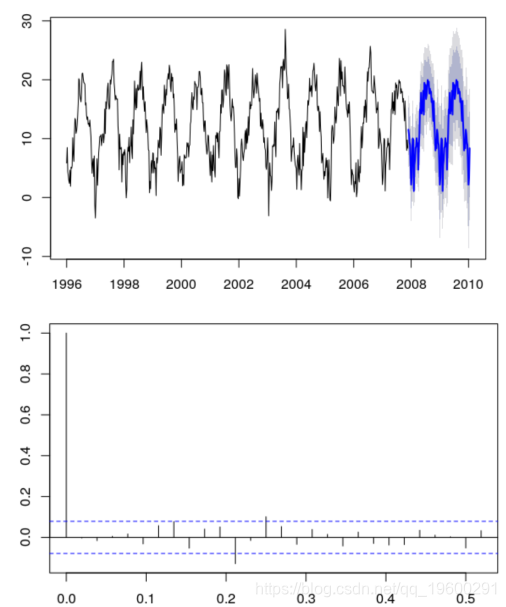
SARIMA模型，s = 52

1.  
    
2.  
   ARIMA = arima (z, order =c(1 ,0 ,0 ,seasonal =list ( order =c(0 ,1 ,0 ,period =52
3.  
   plot ( forecast (ARIMA ,h =112 )

---

最受欢迎的见解

1.在python中使用lstm和pytorch进行时间序列预测

2.python中利用长短期记忆模型lstm进行时间序列预测分析

3.使用r语言进行时间序列（arima，指数平滑）分析

4.r语言多元copula-garch-模型时间序列预测

5.r语言copulas和金融时间序列案例

6.使用r语言随机波动模型sv处理时间序列中的随机波动

7.r语言时间序列tar阈值自回归模型

8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类

9.python3用arima模型进行时间序列预测