拓端数据tecdat|R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析 - 走看看

zoukankan html css js c++ java

拓端数据tecdat|R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析
原文链接：http://tecdat.cn/?p=19469

本文将分析工业指数（DJIA）。工业指数（DIJA）是一个股市指数，表明30家大型上市公司的价值。工业指数（DIJA）的价值基于每个组成公司的每股股票价格之和。

本文将尝试回答的主要问题是：
- 这些年来收益率和交易量如何变化？
- 这些年来，收益率和交易量的波动如何变化？
- 我们如何建模收益率波动？
- 我们如何模拟交易量的波动？
为此，本文按以下内容划分：

第1部分：获取每日和每周对数收益的数据，摘要和图
第2部分：获取每日交易量及其对数比率的数据，摘要和图
第3部分：每日对数收益率分析和GARCH模型定义
第4部分：每日交易量分析和GARCH模型定义



获取数据

利用quantmod软件包中提供的getSymbols（）函数，我们可以获得2007年至2018年底的工业平均指数。
2. getSymbols("^DJI", from = "2007-01-01", to = "2019-01-01")
5. dim(DJI)
7. ## [1] 3020 6
8. class(DJI)
10. ## [1] "xts" "zoo"
让我们看一下DJI xts对象，它提供了六个时间序列，我们可以看到。
2. head(DJI)
4. ## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
5. ## 2007-01-03 12459.54 12580.35 12404.82 12474.52 327200000 12474.52
6. ## 2007-01-04 12473.16 12510.41 12403.86 12480.69 259060000 12480.69
7. ## 2007-01-05 12480.05 12480.13 12365.41 12398.01 235220000 12398.01
8. ## 2007-01-08 12392.01 12445.92 12337.37 12423.49 223500000 12423.49
9. ## 2007-01-09 12424.77 12466.43 12369.17 12416.60 225190000 12416.60
10. ## 2007-01-10 12417.00 12451.61 12355.63 12442.16 226570000 12442.16
11. tail(DJI)
13. ## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
14. ## 2018-12-21 22871.74 23254.59 22396.34 22445.37 900510000 22445.37
15. ## 2018-12-24 22317.28 22339.87 21792.20 21792.20 308420000 21792.20
16. ## 2018-12-26 21857.73 22878.92 21712.53 22878.45 433080000 22878.45
17. ## 2018-12-27 22629.06 23138.89 22267.42 23138.82 407940000 23138.82
18. ## 2018-12-28 23213.61 23381.88 22981.33 23062.40 336510000 23062.40
19. ## 2018-12-31 23153.94 23333.18 23118.30 23327.46 288830000 23327.46
更准确地说，我们有可用的OHLC（开盘，高，低，收盘）指数值，调整后的收盘价和交易量。在这里，我们可以看到生成的相应图表。

我们在此分析调整后的收盘价。
```
DJI[,"DJI.Adjusted"]
```
简单对数收益率

简单的收益定义为：

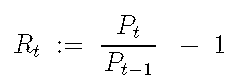
对数收益率定义为：

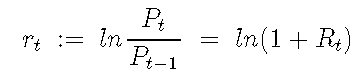
我们计算对数收益率。
```
CalculateReturns(dj_close, method = "log")
```
让我们看看。
2. head(dj_ret)
4. ## DJI.Adjusted
5. ## 2007-01-04 0.0004945580
6. ## 2007-01-05 -0.0066467273
7. ## 2007-01-08 0.0020530973
8. ## 2007-01-09 -0.0005547987
9. ## 2007-01-10 0.0020564627
10. ## 2007-01-11 0.0058356461
11. tail(dj_ret)
13. ## DJI.Adjusted
14. ## 2018-12-21 -0.018286825
15. ## 2018-12-24 -0.029532247
16. ## 2018-12-26 0.048643314
17. ## 2018-12-27 0.011316355
18. ## 2018-12-28 -0.003308137
19. ## 2018-12-31 0.011427645
给出了下面的图。

可以看到波动率的急剧上升和下降。第3部分将对此进行深入验证。

辅助函数

我们需要一些辅助函数来简化一些基本的数据转换，摘要和绘图。

1.从xts转换为带有year and value列的数据框。这样就可以进行年度总结和绘制。
2. df_t <- data.frame(year = factor(year(index(data_xts))), value = coredata(data_xts))
3. colnames(df_t) <- c( "year", "value")
2.摘要统计信息，用于存储为数据框列的数据。
1. rownames(basicStats(rnorm(10,0,1))) # 基本统计数据输出行名称
2. with(dataset, tapply(value, year, basicStats))
3.返回关联的列名。
2. colnames(basicstats[r, which(basicstats[r,] > threshold), drop = FALSE])
4.基于年的面板箱线图。
2. p <- ggplot(data = data, aes(x = year, y = value)) + theme_bw() + theme(legend.position = "none") + geom_boxplot(fill = "blue")
5.密度图，以年份为基准。
2. p <- ggplot(data = data, aes(x = value)) + geom_density(fill = "lightblue")
3. p <- p + facet_wrap(. ~ year)
6.基于年份的QQ图。
2. p <- ggplot(data = dataset, aes(sample = value)) + stat_qq(colour = "blue") + stat_qq_line()
3. p <- p + facet_wrap(. ~ year)
7. Shapiro检验
1. pvalue <- function (v) {
2. shapiro.test(v)$p.value
3. }
每日对数收益率探索性分析

我们将原始的时间序列转换为具有年和值列的数据框。这样可以按年简化绘图和摘要。
2. head(ret_df)
4. ## year value
5. ## 1 2007 0.0004945580
6. ## 2 2007 -0.0066467273
7. ## 3 2007 0.0020530973
8. ## 4 2007 -0.0005547987
9. ## 5 2007 0.0020564627
10. ## 6 2007 0.0058356461
11. tail(ret_df)
13. ## year value
14. ## 3014 2018 -0.018286825
15. ## 3015 2018 -0.029532247
16. ## 3016 2018 0.048643314
17. ## 3017 2018 0.011316355
18. ## 3018 2018 -0.003308137
19. ## 3019 2018 0.011427645
基本统计摘要

给出了基本统计摘要。
3. ## 2007 2008 2009 2010 2011
4. ## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
5. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
6. ## Minimum -0.033488 -0.082005 -0.047286 -0.036700 -0.057061
7. ## Maximum 0.025223 0.105083 0.066116 0.038247 0.041533
8. ## 1. Quartile -0.003802 -0.012993 -0.006897 -0.003853 -0.006193
9. ## 3. Quartile 0.005230 0.007843 0.008248 0.004457 0.006531
10. ## Mean 0.000246 -0.001633 0.000684 0.000415 0.000214
11. ## Median 0.001098 -0.000890 0.001082 0.000681 0.000941
12. ## Sum 0.061427 -0.413050 0.172434 0.104565 0.053810
13. ## SE Mean 0.000582 0.001497 0.000960 0.000641 0.000837
14. ## LCL Mean -0.000900 -0.004580 -0.001207 -0.000848 -0.001434
15. ## UCL Mean 0.001391 0.001315 0.002575 0.001678 0.001861
16. ## Variance 0.000085 0.000567 0.000232 0.000104 0.000176
17. ## Stdev 0.009197 0.023808 0.015242 0.010182 0.013283
18. ## Skewness -0.613828 0.224042 0.070840 -0.174816 -0.526083
19. ## Kurtosis 1.525069 3.670796 2.074240 2.055407 2.453822
20. ## 2012 2013 2014 2015 2016
21. ## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
22. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
23. ## Minimum -0.023910 -0.023695 -0.020988 -0.036402 -0.034473
24. ## Maximum 0.023376 0.023263 0.023982 0.038755 0.024384
25. ## 1. Quartile -0.003896 -0.002812 -0.002621 -0.005283 -0.002845
26. ## 3. Quartile 0.004924 0.004750 0.004230 0.005801 0.004311
27. ## Mean 0.000280 0.000933 0.000288 -0.000090 0.000500
28. ## Median -0.000122 0.001158 0.000728 -0.000211 0.000738
29. ## Sum 0.070054 0.235068 0.072498 -0.022586 0.125884
30. ## SE Mean 0.000470 0.000403 0.000432 0.000613 0.000501
31. ## LCL Mean -0.000645 0.000139 -0.000564 -0.001298 -0.000487
32. ## UCL Mean 0.001206 0.001727 0.001139 0.001118 0.001486
33. ## Variance 0.000055 0.000041 0.000047 0.000095 0.000063
34. ## Stdev 0.007429 0.006399 0.006861 0.009738 0.007951
35. ## Skewness 0.027235 -0.199407 -0.332766 -0.127788 -0.449311
36. ## Kurtosis 0.842890 1.275821 1.073234 1.394268 2.079671
37. ## 2017 2018
38. ## nobs 251.000000 251.000000
39. ## NAs 0.000000 0.000000
40. ## Minimum -0.017930 -0.047143
41. ## Maximum 0.014468 0.048643
42. ## 1. Quartile -0.001404 -0.005017
43. ## 3. Quartile 0.003054 0.005895
44. ## Mean 0.000892 -0.000231
45. ## Median 0.000655 0.000695
46. ## Sum 0.223790 -0.057950
47. ## SE Mean 0.000263 0.000714
48. ## LCL Mean 0.000373 -0.001637
49. ## UCL Mean 0.001410 0.001175
50. ## Variance 0.000017 0.000128
51. ## Stdev 0.004172 0.011313
52. ## Skewness -0.189808 -0.522618
53. ## Kurtosis 2.244076 2.802996
在下文中，我们对上述一些相关指标进行了具体评论。

平均值

每日对数收益率具有正平均值的年份是：
2. filter_stats(stats, "Mean", 0)
4. ## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"
按升序排列。
3. ## 2008 2018 2015 2011 2007 2012 2014
4. ## Mean -0.001633 -0.000231 -9e-05 0.000214 0.000246 0.00028 0.000288
5. ## 2010 2016 2009 2017 2013
6. ## Mean 0.000415 5e-04 0.000684 0.000892 0.000933
中位数

正中位数是：
2. filter_stats(dj_stats, "Median", 0)
4. ## [1] "2007" "2009" "2010" "2011" "2013" "2014" "2016" "2017" "2018"
以升序排列。
3. ## 2008 2015 2012 2017 2010 2018 2014
4. ## Median -0.00089 -0.000211 -0.000122 0.000655 0.000681 0.000695 0.000728
5. ## 2016 2011 2009 2007 2013
6. ## Median 0.000738 0.000941 0.001082 0.001098 0.001158
偏度

偏度（Skewness）可以用来度量随机变量概率分布的不对称性。

公式：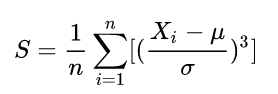

其中是均值，是标准差。

几何意义：

偏度的取值范围为(-∞,+∞)

当偏度<0时，概率分布图左偏（也叫负偏分布，其偏度<0）。

当偏度=0时，表示数据相对均匀的分布在平均值两侧，不一定是绝对的对称分布。

当偏度>0时，概率分布图右偏（也叫正偏分布，其偏度>0）。

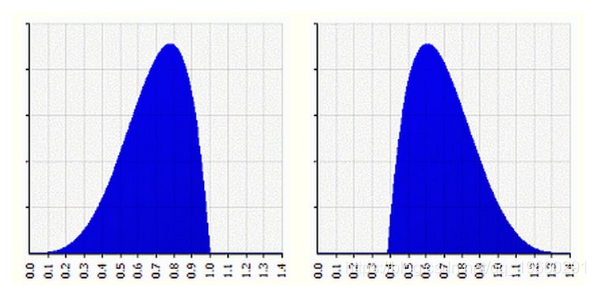
例如上图中，左图形状左偏，右图形状右偏。

每日对数收益出现正偏的年份是：
3. ## [1] "2008" "2009" "2012"
按升序返回对数偏度。
2. stats["Skewness",order(stats["Skewness",
4. ## 2007 2011 2018 2016 2014 2013
5. ## Skewness -0.613828 -0.526083 -0.522618 -0.449311 -0.332766 -0.199407
6. ## 2017 2010 2015 2012 2009 2008
7. ## Skewness -0.189808 -0.174816 -0.127788 0.027235 0.07084 0.224042
峰度

峰度（Kurtosis）可以用来度量随机变量概率分布的陡峭程度。

公式：

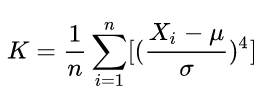
其中是均值，是标准差。

几何意义：

峰度的取值范围为[1,+∞)，完全服从正态分布的数据的峰度值为 3，峰度值越大，概率分布图越高尖，峰度值越小，越矮胖。

例如上图中，左图是标准正太分布，峰度=3，右图的峰度=4，可以看到右图比左图更高尖。

通常我们将峰度值减去3，也被称为超值峰度（Excess Kurtosis），这样正态分布的峰度值等于0，当峰度值>0，则表示该数据分布与正态分布相比较为高尖，当峰度值<0，则表示该数据分布与正态分布相比较为矮胖。

每日对数收益出现超值峰度的年份是：
3. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
4. ## [11] "2017" "2018"
按升序返回超值峰度。
3. ## 2012 2014 2013 2015 2007 2010 2009
4. ## Kurtosis 0.84289 1.073234 1.275821 1.394268 1.525069 2.055407 2.07424
5. ## 2016 2017 2011 2018 2008
6. ## Kurtosis 2.079671 2.244076 2.453822 2.802996 3.670796
2018年的峰度最接近2008年。

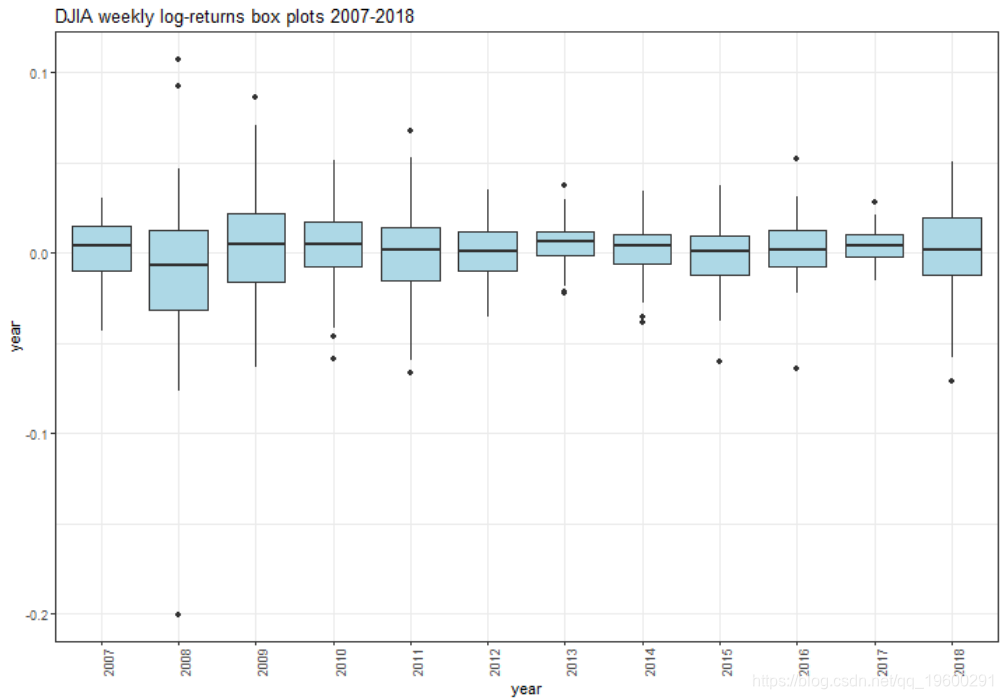
箱形图

我们可以看到2008年出现了最极端的值。从2009年开始，除了2011年和2015年以外，其他所有值的范围都变窄了。但是，与2017年和2018年相比，产生极端值的趋势明显改善。

密度图
```
densityplot(ret_df)
```
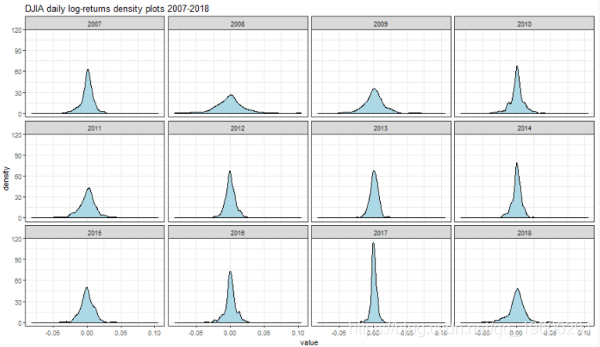
2007年具有显着的负偏。2008年的特点是平坦。2017年的峰值与2018年的平坦度和左偏一致。

shapiro检验
1. shapirot(ret_df)
3. ## result
4. ## 2007 5.989576e-07
5. ## 2008 5.782666e-09
6. ## 2009 1.827967e-05
7. ## 2010 3.897345e-07
8. ## 2011 5.494349e-07
9. ## 2012 1.790685e-02
10. ## 2013 8.102500e-03
11. ## 2014 1.750036e-04
12. ## 2015 5.531137e-03
13. ## 2016 1.511435e-06
14. ## 2017 3.304529e-05
15. ## 2018 1.216327e-07
正常的零假设在2007-2018年的所有年份均被拒绝。

每周对数收益率探索性分析

可以从每日对数收益率开始计算每周对数收益率。让我们假设分析第{t-4，t-3，t-2，t-1，t}天的交易周，并知道第t-5天（前一周的最后一天）的收盘价。我们将每周的对数收益率定义为：

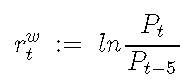
可以写为：

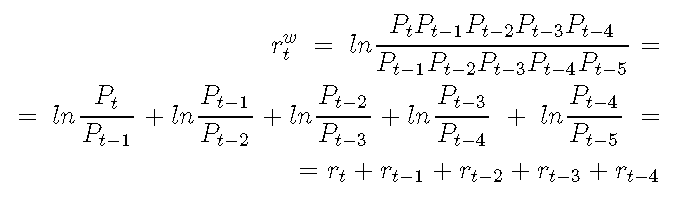
因此，每周对数收益率是应用于交易周窗口的每日对数收益率之和。

我们来看看每周的对数收益率。

该图显示波动率急剧上升和下降。我们将原始时间序列数据转换为数据框。
2. head(weekly_ret_df)
4. ## year value
5. ## 1 2007 -0.0061521694
6. ## 2 2007 0.0126690596
7. ## 3 2007 0.0007523559
8. ## 4 2007 -0.0062677053
9. ## 5 2007 0.0132434177
10. ## 6 2007 -0.0057588519
11. tail(weekly_ret_df)
13. ## year value
14. ## 622 2018 0.05028763
15. ## 623 2018 -0.04605546
16. ## 624 2018 -0.01189714
17. ## 625 2018 -0.07114867
18. ## 626 2018 0.02711928
19. ## 627 2018 0.01142764
基本统计摘要
1. dataframe_basicstats(weekly_ret_df)
3. ## 2007 2008 2009 2010 2011 2012
4. ## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 52.000000
5. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
6. ## Minimum -0.043199 -0.200298 -0.063736 -0.058755 -0.066235 -0.035829
7. ## Maximum 0.030143 0.106977 0.086263 0.051463 0.067788 0.035316
8. ## 1. Quartile -0.009638 -0.031765 -0.015911 -0.007761 -0.015485 -0.010096
9. ## 3. Quartile 0.014808 0.012682 0.022115 0.016971 0.014309 0.011887
10. ## Mean 0.001327 -0.008669 0.003823 0.002011 0.001035 0.001102
11. ## Median 0.004244 -0.006811 0.004633 0.004529 0.001757 0.001166
12. ## Sum 0.069016 -0.450811 0.202605 0.104565 0.053810 0.057303
13. ## SE Mean 0.002613 0.006164 0.004454 0.003031 0.003836 0.002133
14. ## LCL Mean -0.003919 -0.021043 -0.005115 -0.004074 -0.006666 -0.003181
15. ## UCL Mean 0.006573 0.003704 0.012760 0.008096 0.008736 0.005384
16. ## Variance 0.000355 0.001975 0.001051 0.000478 0.000765 0.000237
17. ## Stdev 0.018843 0.044446 0.032424 0.021856 0.027662 0.015382
18. ## Skewness -0.680573 -0.985740 0.121331 -0.601407 -0.076579 -0.027302
19. ## Kurtosis -0.085887 5.446623 -0.033398 0.357708 0.052429 -0.461228
20. ## 2013 2014 2015 2016 2017 2018
21. ## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 53.000000
22. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
23. ## Minimum -0.022556 -0.038482 -0.059991 -0.063897 -0.015317 -0.071149
24. ## Maximum 0.037702 0.034224 0.037693 0.052243 0.028192 0.050288
25. ## 1. Quartile -0.001738 -0.006378 -0.012141 -0.007746 -0.002251 -0.011897
26. ## 3. Quartile 0.011432 0.010244 0.009620 0.012791 0.009891 0.019857
27. ## Mean 0.004651 0.001756 -0.000669 0.002421 0.004304 -0.001093
28. ## Median 0.006360 0.003961 0.000954 0.001947 0.004080 0.001546
29. ## Sum 0.241874 0.091300 -0.035444 0.125884 0.223790 -0.057950
30. ## SE Mean 0.001828 0.002151 0.002609 0.002436 0.001232 0.003592
31. ## LCL Mean 0.000981 -0.002563 -0.005904 -0.002470 0.001830 -0.008302
32. ## UCL Mean 0.008322 0.006075 0.004567 0.007312 0.006778 0.006115
33. ## Variance 0.000174 0.000241 0.000361 0.000309 0.000079 0.000684
34. ## Stdev 0.013185 0.015514 0.018995 0.017568 0.008886 0.026154
35. ## Skewness -0.035175 -0.534403 -0.494963 -0.467158 0.266281 -0.658951
36. ## Kurtosis -0.200282 0.282354 0.665460 2.908942 -0.124341 -0.000870
在下文中，我们对上述一些相关指标进行了具体评论。

平均值

每周对数收益呈正平均值的年份是：
3. ## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"
所有平均值按升序排列。
3. ## 2008 2018 2015 2011 2012 2007 2014
4. ## Mean -0.008669 -0.001093 -0.000669 0.001035 0.001102 0.001327 0.001756
5. ## 2010 2016 2009 2017 2013
6. ## Mean 0.002011 0.002421 0.003823 0.004304 0.004651
中位数

中位数是：
3. ## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016" "2017"
4. ## [11] "2018"
所有中值按升序排列。
3. ## 2008 2015 2012 2018 2011 2016 2014
4. ## Median -0.006811 0.000954 0.001166 0.001546 0.001757 0.001947 0.003961
5. ## 2017 2007 2010 2009 2013
6. ## Median 0.00408 0.004244 0.004529 0.004633 0.00636
偏度

出现正偏的年份是：
1. stats(stats, "Skewness", 0)
3. ## [1] "2009" "2017"
所有偏度按升序排列。
2. stats["Skewness",order(stats["Skewness",,])]
4. ## 2008 2007 2018 2010 2014 2015
5. ## Skewness -0.98574 -0.680573 -0.658951 -0.601407 -0.534403 -0.494963
6. ## 2016 2011 2013 2012 2009 2017
7. ## Skewness -0.467158 -0.076579 -0.035175 -0.027302 0.121331 0.266281
峰度

出现正峰度的年份是：
2. filter_stats(stats, "Kurtosis", 0)
4. ## [1] "2008" "2010" "2011" "2014" "2015" "2016"
峰度值都按升序排列。
3. ## 2012 2013 2017 2007 2009 2018
4. ## Kurtosis -0.461228 -0.200282 -0.124341 -0.085887 -0.033398 -0.00087
5. ## 2011 2014 2010 2015 2016 2008
6. ## Kurtosis 0.052429 0.282354 0.357708 0.66546 2.908942 5.446623
2008年也是每周峰度最高的年份。但是，在这种情况下，2017年的峰度为负，而2016年的峰度为第二。

箱形图

 密度图

 shapiro检验
2. shapirot(weekly_df)
4. ## result
5. ## 2007 0.0140590311
6. ## 2008 0.0001397267
7. ## 2009 0.8701335006
8. ## 2010 0.0927104389
9. ## 2011 0.8650874270
10. ## 2012 0.9934600084
11. ## 2013 0.4849043121
12. ## 2014 0.1123139646
13. ## 2015 0.3141519756
14. ## 2016 0.0115380989
15. ## 2017 0.9465281164
16. ## 2018 0.0475141869
零假设在2007、2008、2016年被拒绝。

QQ图

在2008年尤其明显地违背正态分布的情况。

交易量探索性分析

在这一部分中，本文将分析道琼斯工业平均指数（DJIA）的交易量。

获取数据

 每日量探索性分析

我们绘制每日交易量。
1. vol <- DJI[,"DJI.Volume"]
2. plot(vol)
值得注意的是，2017年初的水平跃升，我们将在第4部分中进行研究。我们将时间序列数据和时间轴索引转换为数据框。
2. head(dj_vol_df)
4. ## year value
5. ## 1 2007 327200000
6. ## 2 2007 259060000
7. ## 3 2007 235220000
8. ## 4 2007 223500000
9. ## 5 2007 225190000
10. ## 6 2007 226570000
11. tail(dj_vol_df)
13. ## year value
14. ## 3015 2018 900510000
15. ## 3016 2018 308420000
16. ## 3017 2018 433080000
17. ## 3018 2018 407940000
18. ## 3019 2018 336510000
19. ## 3020 2018 288830000
基本统计摘要
2. ## 2007 2008 2009 2010
3. ## nobs 2.510000e+02 2.530000e+02 2.520000e+02 2.520000e+02
4. ## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
5. ## Minimum 8.640000e+07 6.693000e+07 5.267000e+07 6.840000e+07
6. ## Maximum 4.571500e+08 6.749200e+08 6.729500e+08 4.598900e+08
7. ## 1. Quartile 2.063000e+08 2.132100e+08 1.961850e+08 1.633400e+08
8. ## 3. Quartile 2.727400e+08 3.210100e+08 3.353625e+08 2.219025e+08
9. ## Mean 2.449575e+08 2.767164e+08 2.800537e+08 2.017934e+08
10. ## Median 2.350900e+08 2.569700e+08 2.443200e+08 1.905050e+08
11. ## Sum 6.148432e+10 7.000924e+10 7.057354e+10 5.085193e+10
12. ## SE Mean 3.842261e+06 5.965786e+06 7.289666e+06 3.950031e+06
13. ## LCL Mean 2.373901e+08 2.649672e+08 2.656970e+08 1.940139e+08
14. ## UCL Mean 2.525248e+08 2.884655e+08 2.944104e+08 2.095728e+08
15. ## Variance 3.705505e+15 9.004422e+15 1.339109e+16 3.931891e+15
16. ## Stdev 6.087286e+07 9.489163e+07 1.157199e+08 6.270480e+07
17. ## Skewness 9.422400e-01 1.203283e+00 1.037015e+00 1.452082e+00
18. ## Kurtosis 1.482540e+00 2.064821e+00 6.584810e-01 3.214065e+00
19. ## 2011 2012 2013 2014
20. ## nobs 2.520000e+02 2.500000e+02 2.520000e+02 2.520000e+02
21. ## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
22. ## Minimum 8.410000e+06 4.771000e+07 3.364000e+07 4.287000e+07
23. ## Maximum 4.799800e+08 4.296100e+08 4.200800e+08 6.554500e+08
24. ## 1. Quartile 1.458775e+08 1.107150e+08 9.488000e+07 7.283000e+07
25. ## 3. Quartile 1.932400e+08 1.421775e+08 1.297575e+08 9.928000e+07
26. ## Mean 1.804133e+08 1.312606e+08 1.184434e+08 9.288516e+07
27. ## Median 1.671250e+08 1.251950e+08 1.109250e+08 8.144500e+07
28. ## Sum 4.546415e+10 3.281515e+10 2.984773e+10 2.340706e+10
29. ## SE Mean 3.897738e+06 2.796503e+06 2.809128e+06 3.282643e+06
30. ## LCL Mean 1.727369e+08 1.257528e+08 1.129109e+08 8.642012e+07
31. ## UCL Mean 1.880897e+08 1.367684e+08 1.239758e+08 9.935019e+07
32. ## Variance 3.828475e+15 1.955108e+15 1.988583e+15 2.715488e+15
33. ## Stdev 6.187468e+07 4.421660e+07 4.459353e+07 5.211034e+07
34. ## Skewness 1.878239e+00 3.454971e+00 3.551752e+00 6.619268e+00
35. ## Kurtosis 5.631080e+00 1.852581e+01 1.900989e+01 5.856136e+01
36. ## 2015 2016 2017 2018
37. ## nobs 2.520000e+02 2.520000e+02 2.510000e+02 2.510000e+02
38. ## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
39. ## Minimum 4.035000e+07 4.589000e+07 1.186100e+08 1.559400e+08
40. ## Maximum 3.445600e+08 5.734700e+08 6.357400e+08 9.005100e+08
41. ## 1. Quartile 8.775250e+07 8.224250e+07 2.695850e+08 2.819550e+08
42. ## 3. Quartile 1.192150e+08 1.203550e+08 3.389950e+08 4.179200e+08
43. ## Mean 1.093957e+08 1.172089e+08 3.112396e+08 3.593710e+08
44. ## Median 1.021000e+08 9.410500e+07 2.996700e+08 3.414700e+08
45. ## Sum 2.756772e+10 2.953664e+10 7.812114e+10 9.020213e+10
46. ## SE Mean 2.433611e+06 4.331290e+06 4.376432e+06 6.984484e+06
47. ## LCL Mean 1.046028e+08 1.086786e+08 3.026202e+08 3.456151e+08
48. ## UCL Mean 1.141886e+08 1.257392e+08 3.198590e+08 3.731270e+08
49. ## Variance 1.492461e+15 4.727538e+15 4.807442e+15 1.224454e+16
50. ## Stdev 3.863238e+07 6.875709e+07 6.933572e+07 1.106550e+08
51. ## Skewness 3.420032e+00 3.046742e+00 1.478708e+00 1.363823e+00
52. ## Kurtosis 1.612326e+01 1.122161e+01 3.848619e+00 3.277164e+00
在下文中，我们对上面显示的一些相关指标进行了评论。

平均值

每日交易量具有正平均值的年份是：
3. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
4. ## [11] "2017" "2018"
所有每日交易量均值按升序排列。
3. ## 2014 2015 2016 2013 2012 2011 2010
4. ## Mean 92885159 109395714 117208889 118443373 131260600 180413294 201793373
5. ## 2007 2008 2009 2017 2018
6. ## Mean 244957450 276716364 280053730 311239602 359371036
中位数

每日交易量中位数为正的年份是：
3. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
4. ## [11] "2017" "2018"
所有每日成交量中值均按升序排列。
3. ## 2014 2016 2015 2013 2012 2011 2010
4. ## Median 81445000 94105000 102100000 110925000 125195000 167125000 190505000
5. ## 2007 2009 2008 2017 2018
6. ## Median 235090000 244320000 256970000 299670000 341470000
偏度

每日交易量出现正偏的年份是：
3. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
4. ## [11] "2017" "2018"
每日交易量偏度值均按升序排列。
3. ## 2007 2009 2008 2018 2010 2017 2011
4. ## Skewness 0.94224 1.037015 1.203283 1.363823 1.452082 1.478708 1.878239
5. ## 2016 2015 2012 2013 2014
6. ## Skewness 3.046742 3.420032 3.454971 3.551752 6.619268
峰度

有正峰度的年份是：
3. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
4. ## [11] "2017" "2018"
按升序排列。
2. ## 2009 2007 2008 2010 2018 2017 2011
3. ## Kurtosis 0.658481 1.48254 2.064821 3.214065 3.277164 3.848619 5.63108
4. ## 2016 2015 2012 2013 2014
5. ## Kurtosis 11.22161 16.12326 18.52581 19.00989 58.56136
箱形图

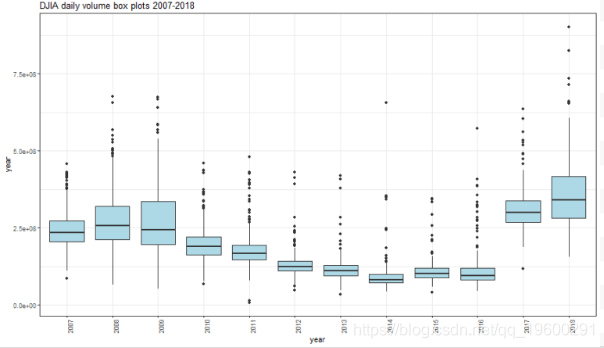
从2010年开始交易量开始下降，2017年出现了显着增长。2018年的交易量甚至超过了2017年和其他年份。

密度图

 shapiro检验
1. ## result
2. ## 2007 6.608332e-09
3. ## 2008 3.555102e-10
4. ## 2009 1.023147e-10
5. ## 2010 9.890576e-13
6. ## 2011 2.681476e-16
7. ## 2012 1.866544e-20
8. ## 2013 6.906596e-21
9. ## 2014 5.304227e-27
10. ## 2015 2.739912e-21
11. ## 2016 6.640215e-23
12. ## 2017 4.543843e-12
13. ## 2018 9.288371e-11
正态分布的零假设被拒绝。

QQ图

QQplots直观地确认了每日交易量分布的非正态情况。

每日交易量对数比率探索性分析

与对数收益类似，我们可以将交易量对数比率定义为

vt：= ln(Vt/Vt−1)
我们可以通过PerformanceAnalytics包中的CalculateReturns对其进行计算并将其绘制出来。
```
plot(vol_log_ratio)
```
将交易量对数比率时间序列数据和时间轴索引映射到数据框。
1. head(dvol_df)
3. ## year value
4. ## 1 2007 -0.233511910
5. ## 2 2007 -0.096538449
6. ## 3 2007 -0.051109832
7. ## 4 2007 0.007533076
8. ## 5 2007 0.006109458
9. ## 6 2007 0.144221282
10. tail(vol_df)
12. ## year value
13. ## 3014 2018 0.44563907
14. ## 3015 2018 -1.07149878
15. ## 3016 2018 0.33945998
16. ## 3017 2018 -0.05980236
17. ## 3018 2018 -0.19249224
18. ## 3019 2018 -0.15278959
基本统计摘要
2. ## 2007 2008 2009 2010 2011
3. ## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
4. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
5. ## Minimum -1.606192 -1.122526 -1.071225 -1.050181 -2.301514
6. ## Maximum 0.775961 0.724762 0.881352 1.041216 2.441882
7. ## 1. Quartile -0.123124 -0.128815 -0.162191 -0.170486 -0.157758
8. ## 3. Quartile 0.130056 0.145512 0.169233 0.179903 0.137108
9. ## Mean -0.002685 0.001203 -0.001973 -0.001550 0.000140
10. ## Median -0.010972 0.002222 -0.031748 -0.004217 -0.012839
11. ## Sum -0.671142 0.304462 -0.497073 -0.390677 0.035162
12. ## SE Mean 0.016984 0.016196 0.017618 0.019318 0.026038
13. ## LCL Mean -0.036135 -0.030693 -0.036670 -0.039596 -0.051141
14. ## UCL Mean 0.030766 0.033100 0.032725 0.036495 0.051420
15. ## Variance 0.072112 0.066364 0.078219 0.094041 0.170850
16. ## Stdev 0.268536 0.257612 0.279677 0.306661 0.413341
17. ## Skewness -0.802037 -0.632586 0.066535 -0.150523 0.407226
18. ## Kurtosis 5.345212 2.616615 1.500979 1.353797 14.554642
19. ## 2012 2013 2014 2015 2016
20. ## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
21. ## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
22. ## Minimum -2.158960 -1.386215 -2.110572 -1.326016 -1.336471
23. ## Maximum 1.292956 1.245202 2.008667 1.130289 1.319713
24. ## 1. Quartile -0.152899 -0.145444 -0.144280 -0.143969 -0.134011
25. ## 3. Quartile 0.144257 0.149787 0.134198 0.150003 0.141287
26. ## Mean 0.001642 -0.002442 0.000200 0.000488 0.004228
27. ## Median -0.000010 -0.004922 0.013460 0.004112 -0.002044
28. ## Sum 0.410521 -0.615419 0.050506 0.123080 1.065480
29. ## SE Mean 0.021293 0.019799 0.023514 0.019010 0.019089
30. ## LCL Mean -0.040295 -0.041435 -0.046110 -0.036952 -0.033367
31. ## UCL Mean 0.043579 0.036551 0.046510 0.037929 0.041823
32. ## Variance 0.113345 0.098784 0.139334 0.091071 0.091826
33. ## Stdev 0.336667 0.314299 0.373274 0.301780 0.303028
34. ## Skewness -0.878227 -0.297951 -0.209417 -0.285918 0.083826
35. ## Kurtosis 8.115847 4.681120 9.850061 4.754926 4.647785
36. ## 2017 2018
37. ## nobs 251.000000 251.000000
38. ## NAs 0.000000 0.000000
39. ## Minimum -0.817978 -1.071499
40. ## Maximum 0.915599 0.926101
41. ## 1. Quartile -0.112190 -0.119086
42. ## 3. Quartile 0.110989 0.112424
43. ## Mean -0.000017 0.000257
44. ## Median -0.006322 0.003987
45. ## Sum -0.004238 0.064605
46. ## SE Mean 0.013446 0.014180
47. ## LCL Mean -0.026500 -0.027671
48. ## UCL Mean 0.026466 0.028185
49. ## Variance 0.045383 0.050471
50. ## Stdev 0.213032 0.224658
51. ## Skewness 0.088511 -0.281007
52. ## Kurtosis 3.411036 4.335748
在下文中，我们对一些相关的上述指标进行了具体评论。

平均值

每日交易量对数比率具有正平均值的年份是：
2. ## [1] "2008" "2011" "2012" "2014" "2015" "2016" "2018"
所有每日成交量比率的平均值均按升序排列。
1. ## 2007 2013 2009 2010 2017 2011 2014
2. ## Mean -0.002685 -0.002442 -0.001973 -0.00155 -1.7e-05 0.00014 2e-04
3. ## 2018 2015 2008 2012 2016
4. ## Mean 0.000257 0.000488 0.001203 0.001642 0.004228
中位数

每日交易量对数比率具有正中位数的年份是：
```
## [1] "2008" "2014" "2015" "2018"
```
道琼斯所有每日成交量比率的中位数均按升序排列。
1. ## 2009 2011 2007 2017 2013 2010
2. ## Median -0.031748 -0.012839 -0.010972 -0.006322 -0.004922 -0.004217
3. ## 2016 2012 2008 2018 2015 2014
4. ## Median -0.002044 -1e-05 0.002222 0.003987 0.004112 0.01346
偏度

每日成交量比率具有正偏的年份是：
```
## [1] "2009" "2011" "2016" "2017"
```
所有每日成交量比率的平均值均按升序排列。
1. ## 2012 2007 2008 2013 2015 2018
2. ## Skewness -0.878227 -0.802037 -0.632586 -0.297951 -0.285918 -0.281007
3. ## 2014 2010 2009 2016 2017 2011
4. ## Skewness -0.209417 -0.150523 0.066535 0.083826 0.088511 0.407226
峰度

有正峰度的年份是：
1. ## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
2. ## [11] "2017" "2018"
均按升序排列。
1. ## 2010 2009 2008 2017 2018 2016 2013
2. ## Kurtosis 1.353797 1.500979 2.616615 3.411036 4.335748 4.647785 4.68112
3. ## 2015 2007 2012 2014 2011
4. ## Kurtosis 4.754926 5.345212 8.115847 9.850061 14.55464
箱形图

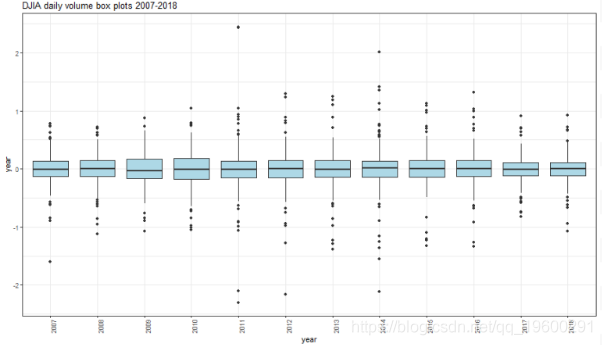
可以在2011、2014和2016年发现正的极端值。在2007、2011、2012、2014年可以发现负的极端值。

密度图

 shapiro检验
1. ## result
2. ## 2007 3.695053e-09
3. ## 2008 6.160136e-07
4. ## 2009 2.083475e-04
5. ## 2010 1.500060e-03
6. ## 2011 3.434415e-18
7. ## 2012 8.417627e-12
8. ## 2013 1.165184e-10
9. ## 2014 1.954662e-16
10. ## 2015 5.261037e-11
11. ## 2016 7.144940e-11
12. ## 2017 1.551041e-08
13. ## 2018 3.069196e-09
基于报告的p值，我们可以拒绝所有正态分布的零假设。

QQ图

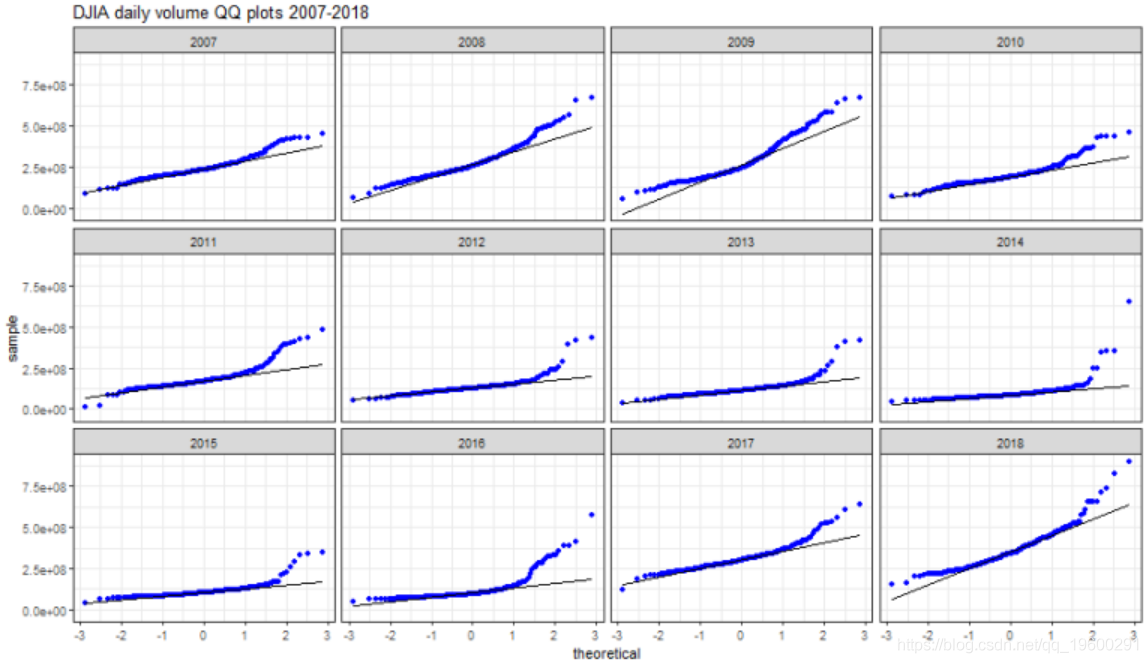
在所有报告的年份都可以发现偏离正态状态。

对数收益率GARCH模型

我将为工业平均指数（DJIA）的每日对数收益率建立一个ARMA-GARCH模型。

这是工业平均指数每日对数收益的图。
```
plot(ret)
```
离群值检测

Performance Analytics程序包中的Return.clean函数能够清除异常值。在下面，我们将原始时间序列与调整离群值后的进行比较。
```
clean(ret, "boudt")
```
作为对波动率评估的更为保守的方法，本文将以原始时间序列进行分析。

相关图

以下是自相关和偏相关图。
```
acf(ret)
```
```
pacf(dj_ret)
```
上面的相关图表明p和q> 0的一些ARMA（p，q）模型。将在本分析的该范围内对此进行验证。

单位根检验

我们运行Augmented Dickey-Fuller检验。
2. ##
3. ## ###############################################
4. ## # Augmented Dickey-Fuller Test Unit Root Test #
5. ## ###############################################
6. ##
7. ## Test regression none
8. ##
9. ##
10. ## Call:
11. ## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
12. ##
13. ## Residuals:
14. ## Min 1Q Median 3Q Max
15. ## -0.081477 -0.004141 0.000762 0.005426 0.098777
16. ##
17. ## Coefficients:
18. ## Estimate Std. Error t value Pr(>|t|)
19. ## z.lag.1 -1.16233 0.02699 -43.058 < 2e-16 ***
20. ## z.diff.lag 0.06325 0.01826 3.464 0.000539 ***
21. ## ---
22. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
23. ##
24. ## Residual standard error: 0.01157 on 2988 degrees of freedom
25. ## Multiple R-squared: 0.5484, Adjusted R-squared: 0.5481
26. ## F-statistic: 1814 on 2 and 2988 DF, p-value: < 2.2e-16
27. ##
28. ##
29. ## Value of test-statistic is: -43.0578
30. ##
31. ## Critical values for test statistics:
32. ## 1pct 5pct 10pct
33. ## tau1 -2.58 -1.95 -1.62
基于报告的检验统计数据与临界值的比较，我们拒绝单位根存在的零假设。

ARMA模型

现在，我们确定时间序列的ARMA结构，以便对结果残差进行ARCH效应检验。ACF和PACF系数拖尾表明存在ARMA（2,2）。我们利用auto.arima（）函数开始构建。
1. ## Series: ret
2. ## ARIMA(2,0,4) with zero mean
3. ##
4. ## Coefficients:
5. ## ar1 ar2 ma1 ma2 ma3 ma4
6. ## 0.4250 -0.8784 -0.5202 0.8705 -0.0335 -0.0769
7. ## s.e. 0.0376 0.0628 0.0412 0.0672 0.0246 0.0203
8. ##
9. ## sigma^2 estimated as 0.0001322: log likelihood=9201.19
10. ## AIC=-18388.38 AICc=-18388.34 BIC=-18346.29
11. ##
12. ## Training set error measures:
13. ## ME RMSE MAE MPE MAPE MASE
14. ## Training set 0.0002416895 0.01148496 0.007505056 NaN Inf 0.6687536
15. ## ACF1
16. ## Training set -0.002537238
建议使用ARMA（2,4）模型。但是，ma3系数在统计上并不显着，进一步通过以下方法验证：
1. ## z test of coefficients:
2. ##
3. ## Estimate Std. Error z value Pr(>|z|)
4. ## ar1 0.425015 0.037610 11.3007 < 2.2e-16 ***
5. ## ar2 -0.878356 0.062839 -13.9779 < 2.2e-16 ***
6. ## ma1 -0.520173 0.041217 -12.6204 < 2.2e-16 ***
7. ## ma2 0.870457 0.067211 12.9511 < 2.2e-16 ***
8. ## ma3 -0.033527 0.024641 -1.3606 0.1736335
9. ## ma4 -0.076882 0.020273 -3.7923 0.0001492 ***
10. ## ---
11. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
因此，我们将MA阶q <= 2作为约束。
1. ## Series: dj_ret
2. ## ARIMA(2,0,2) with zero mean
3. ##
4. ## Coefficients:
5. ## ar1 ar2 ma1 ma2
6. ## -0.5143 -0.4364 0.4212 0.3441
7. ## s.e. 0.1461 0.1439 0.1512 0.1532
8. ##
9. ## sigma^2 estimated as 0.0001325: log likelihood=9196.33
10. ## AIC=-18382.66 AICc=-18382.64 BIC=-18352.6
11. ##
12. ## Training set error measures:
13. ## ME RMSE MAE MPE MAPE MASE
14. ## Training set 0.0002287171 0.01150361 0.007501925 Inf Inf 0.6684746
15. ## ACF1
16. ## Training set -0.002414944
现在，所有系数都具有统计意义。
1. ## z test of coefficients:
2. ##
3. ## Estimate Std. Error z value Pr(>|z|)
4. ## ar1 -0.51428 0.14613 -3.5192 0.0004328 ***
5. ## ar2 -0.43640 0.14392 -3.0322 0.0024276 **
6. ## ma1 0.42116 0.15121 2.7853 0.0053485 **
7. ## ma2 0.34414 0.15323 2.2458 0.0247139 *
8. ## ---
9. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
使用ARMA（2,1）和ARMA（1,2）进行的进一步验证得出的AIC值高于ARMA（2,2）。因此，ARMA（2,2）是更可取的。这是结果。
1. ## Series: dj_ret
2. ## ARIMA(2,0,1) with zero mean
3. ##
4. ## Coefficients:
5. ## ar1 ar2 ma1
6. ## -0.4619 -0.1020 0.3646
7. ## s.e. 0.1439 0.0204 0.1438
8. ##
9. ## sigma^2 estimated as 0.0001327: log likelihood=9194.1
10. ## AIC=-18380.2 AICc=-18380.19 BIC=-18356.15
11. ##
12. ## Training set error measures:
13. ## ME RMSE MAE MPE MAPE MASE
14. ## Training set 0.0002370597 0.01151213 0.007522059 Inf Inf 0.6702687
15. ## ACF1
16. ## Training set 0.0009366271
17. coeftest(auto_model3)
19. ##
20. ## z test of coefficients:
21. ##
22. ## Estimate Std. Error z value Pr(>|z|)
23. ## ar1 -0.461916 0.143880 -3.2104 0.001325 **
24. ## ar2 -0.102012 0.020377 -5.0062 5.552e-07 ***
25. ## ma1 0.364628 0.143818 2.5353 0.011234 *
26. ## ---
27. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
所有系数均具有统计学意义。
2. ## ARIMA(1,0,2) with zero mean
3. ##
4. ## Coefficients:
5. ## ar1 ma1 ma2
6. ## -0.4207 0.3259 -0.0954
7. ## s.e. 0.1488 0.1481 0.0198
8. ##
9. ## sigma^2 estimated as 0.0001328: log likelihood=9193.01
10. ## AIC=-18378.02 AICc=-18378 BIC=-18353.96
11. ##
12. ## Training set error measures:
13. ## ME RMSE MAE MPE MAPE MASE
14. ## Training set 0.0002387398 0.0115163 0.007522913 Inf Inf 0.6703448
15. ## ACF1
16. ## Training set -0.001958194
17. coeftest(auto_model4)
19. ##
20. ## z test of coefficients:
21. ##
22. ## Estimate Std. Error z value Pr(>|z|)
23. ## ar1 -0.420678 0.148818 -2.8268 0.004702 **
24. ## ma1 0.325918 0.148115 2.2004 0.027776 *
25. ## ma2 -0.095407 0.019848 -4.8070 1.532e-06 ***
26. ## ---
27. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
所有系数均具有统计学意义。此外，我们使用TSA软件包报告中的eacf（）函数。
1. ## AR/MA
2. ## 0 1 2 3 4 5 6 7 8 9 10 11 12 13
3. ## 0 x x x o x o o o o o o o o x
4. ## 1 x x o o x o o o o o o o o o
5. ## 2 x o o x x o o o o o o o o o
6. ## 3 x o x o x o o o o o o o o o
7. ## 4 x x x x x o o o o o o o o o
8. ## 5 x x x x x o o x o o o o o o
9. ## 6 x x x x x x o o o o o o o o
10. ## 7 x x x x x o o o o o o o o o
以“ O”为顶点的左上三角形位于（p，q）= {（1,2 ,,（2,2），（1,3）}}内，它表示一组潜在候选对象（p，q）值。ARMA（1,2）模型已经过验证。ARMA（2,2）已经是候选模型。让我们验证ARMA（1,3）。
1. ## Call:
2. ##
3. ## Coefficients:
4. ## ar1 ma1 ma2 ma3
5. ## -0.2057 0.1106 -0.0681 0.0338
6. ## s.e. 0.2012 0.2005 0.0263 0.0215
7. ##
8. ## sigma^2 estimated as 0.0001325: log likelihood = 9193.97, aic = -18379.94
9. coeftest(arima_model5)
11. ##
12. ## z test of coefficients:
13. ##
14. ## Estimate Std. Error z value Pr(>|z|)
15. ## ar1 -0.205742 0.201180 -1.0227 0.306461
16. ## ma1 0.110599 0.200475 0.5517 0.581167
17. ## ma2 -0.068124 0.026321 -2.5882 0.009647 **
18. ## ma3 0.033832 0.021495 1.5739 0.115501
19. ## ---
20. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
只有一个系数具有统计意义。

结论是，我们选择ARMA（2,2）作为均值模型。现在，我们可以继续进行ARCH效果检验。

ARCH效应检验

现在，我们可以检验模型残差上是否存在ARCH效应。如果ARCH效应对于我们的时间序列的残差在统计上显着，则需要GARCH模型。
2. ## ARCH LM-test; Null hypothesis: no ARCH effects
3. ##
4. ## data: model_residuals - mean(model_residuals)
5. ## Chi-squared = 986.82, df = 12, p-value < 2.2e-16
基于报告的p值，我们拒绝没有ARCH效应的原假设。

让我们看一下残差相关图。

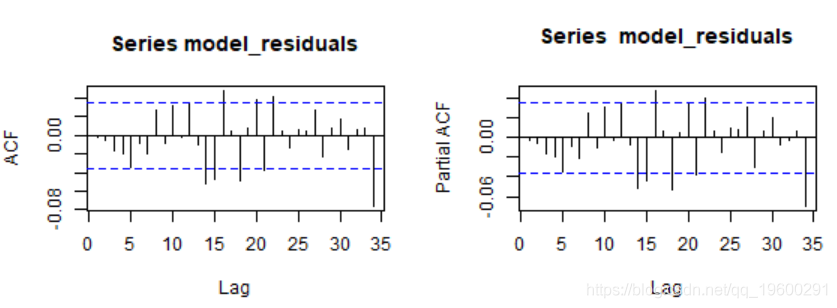
条件波动率

条件均值和方差定义为：

μt：= E（rt | Ft-1）σt2：= Var（rt | Ft-1）= E [（rt-μt）2 | Ft-1]

条件波动率可以计算为条件方差的平方根。

eGARCH模型

将sGARCH作为方差模型的尝试未获得具有统计显着性系数的结果。而指数GARCH（eGARCH）方差模型能够捕获波动率内的不对称性。要检查DJIA对数收益率内的不对称性，显示汇总统计数据和密度图。
1. ## DAdjusted
2. ## nobs 3019.000000
3. ## NAs 0.000000
4. ## Minimum -0.082005
5. ## Maximum 0.105083
6. ## 1. Quartile -0.003991
7. ## 3. Quartile 0.005232
8. ## Mean 0.000207
9. ## Median 0.000551
10. ## Sum 0.625943
11. ## SE Mean 0.000211
12. ## LCL Mean -0.000206
13. ## UCL Mean 0.000621
14. ## Variance 0.000134
15. ## Stdev 0.011593
16. ## Skewness -0.141370
17. ## Kurtosis 10.200492
负偏度值确认分布内不对称性的存在。

这给出了密度图。

我们继续提出eGARCH模型作为方差模型（针对条件方差）。更准确地说，我们将使用ARMA（2,2）作为均值模型，指数GARCH（1,1）作为方差模型对ARMA-GARCH进行建模。

在此之前，我们进一步强调ARMA（0,0）在这种情况下不令人满意。ARMA-GARCH：ARMA（0,0）+ eGARCH（1,1）
1. ##
2. ## *---------------------------------*
3. ## * GARCH Model Fit *
4. ## *---------------------------------*
5. ##
6. ## Conditional Variance Dynamics
7. ## -----------------------------------
8. ## GARCH Model : eGARCH(1,1)
9. ## Mean Model : ARFIMA(0,0,0)
10. ## Distribution : sstd
11. ##
12. ## Optimal Parameters
13. ## ------------------------------------
14. ## Estimate Std. Error t value Pr(>|t|)
15. ## mu 0.000303 0.000117 2.5933 0.009506
16. ## omega -0.291302 0.016580 -17.5699 0.000000
17. ## alpha1 -0.174456 0.013913 -12.5387 0.000000
18. ## beta1 0.969255 0.001770 547.6539 0.000000
19. ## gamma1 0.188918 0.021771 8.6773 0.000000
20. ## skew 0.870191 0.021763 39.9848 0.000000
21. ## shape 6.118380 0.750114 8.1566 0.000000
22. ##
23. ## Robust Standard Errors:
24. ## Estimate Std. Error t value Pr(>|t|)
25. ## mu 0.000303 0.000130 2.3253 0.020055
26. ## omega -0.291302 0.014819 -19.6569 0.000000
27. ## alpha1 -0.174456 0.016852 -10.3524 0.000000
28. ## beta1 0.969255 0.001629 595.0143 0.000000
29. ## gamma1 0.188918 0.031453 6.0063 0.000000
30. ## skew 0.870191 0.022733 38.2783 0.000000
31. ## shape 6.118380 0.834724 7.3298 0.000000
32. ##
33. ## LogLikelihood : 10138.63
34. ##
35. ## Information Criteria
36. ## ------------------------------------
37. ##
38. ## Akaike -6.7119
39. ## Bayes -6.6980
40. ## Shibata -6.7119
41. ## Hannan-Quinn -6.7069
42. ##
43. ## Weighted Ljung-Box Test on Standardized Residuals
44. ## ------------------------------------
45. ## statistic p-value
46. ## Lag[1] 5.475 0.01929
47. ## Lag[2*(p+q)+(p+q)-1][2] 6.011 0.02185
48. ## Lag[4*(p+q)+(p+q)-1][5] 7.712 0.03472
49. ## d.o.f=0
50. ## H0 : No serial correlation
51. ##
52. ## Weighted Ljung-Box Test on Standardized Squared Residuals
53. ## ------------------------------------
54. ## statistic p-value
55. ## Lag[1] 1.342 0.2467
56. ## Lag[2*(p+q)+(p+q)-1][5] 2.325 0.5438
57. ## Lag[4*(p+q)+(p+q)-1][9] 2.971 0.7638
58. ## d.o.f=2
59. ##
60. ## Weighted ARCH LM Tests
61. ## ------------------------------------
62. ## Statistic Shape Scale P-Value
63. ## ARCH Lag[3] 0.3229 0.500 2.000 0.5699
64. ## ARCH Lag[5] 1.4809 1.440 1.667 0.5973
65. ## ARCH Lag[7] 1.6994 2.315 1.543 0.7806
66. ##
67. ## Nyblom stability test
68. ## ------------------------------------
69. ## Joint Statistic: 4.0468
70. ## Individual Statistics:
71. ## mu 0.2156
72. ## omega 1.0830
73. ## alpha1 0.5748
74. ## beta1 0.8663
75. ## gamma1 0.3994
76. ## skew 0.1044
77. ## shape 0.4940
78. ##
79. ## Asymptotic Critical Values (10% 5% 1%)
80. ## Joint Statistic: 1.69 1.9 2.35
81. ## Individual Statistic: 0.35 0.47 0.75
82. ##
83. ## Sign Bias Test
84. ## ------------------------------------
85. ## t-value prob sig
86. ## Sign Bias 1.183 0.23680
87. ## Negative Sign Bias 2.180 0.02932 **
88. ## Positive Sign Bias 1.554 0.12022
89. ## Joint Effect 8.498 0.03677 **
90. ##
91. ##
92. ## Adjusted Pearson Goodness-of-Fit Test:
93. ## ------------------------------------
94. ## group statistic p-value(g-1)
95. ## 1 20 37.24 0.00741
96. ## 2 30 42.92 0.04633
97. ## 3 40 52.86 0.06831
98. ## 4 50 65.55 0.05714
99. ##
100. ##
101. ## Elapsed time : 0.6527421
所有系数均具有统计学意义。但是，根据以上报告的p值的标准化残差加权Ljung-Box检验，我们确认该模型无法捕获所有ARCH效果（我们拒绝了残差内无相关性的零假设））。

作为结论，我们通过在下面所示的GARCH拟合中指定ARMA（2,2）作为均值模型来继续进行。

ARMA-GARCH：ARMA（2,2）+ eGARCH（1,1）
1. ##
2. ## *---------------------------------*
3. ## * GARCH Model Fit *
4. ## *---------------------------------*
5. ##
6. ## Conditional Variance Dynamics
7. ## -----------------------------------
8. ## GARCH Model : eGARCH(1,1)
9. ## Mean Model : ARFIMA(2,0,2)
10. ## Distribution : sstd
11. ##
12. ## Optimal Parameters
13. ## ------------------------------------
14. ## Estimate Std. Error t value Pr(>|t|)
15. ## ar1 -0.47642 0.026115 -18.2433 0
16. ## ar2 -0.57465 0.052469 -10.9523 0
17. ## ma1 0.42945 0.025846 16.6157 0
18. ## ma2 0.56258 0.054060 10.4066 0
19. ## omega -0.31340 0.003497 -89.6286 0
20. ## alpha1 -0.17372 0.011642 -14.9222 0
21. ## beta1 0.96598 0.000027 35240.1590 0
22. ## gamma1 0.18937 0.011893 15.9222 0
23. ## skew 0.84959 0.020063 42.3469 0
24. ## shape 5.99161 0.701313 8.5434 0
25. ##
26. ## Robust Standard Errors:
27. ## Estimate Std. Error t value Pr(>|t|)
28. ## ar1 -0.47642 0.007708 -61.8064 0
29. ## ar2 -0.57465 0.018561 -30.9608 0
30. ## ma1 0.42945 0.007927 54.1760 0
31. ## ma2 0.56258 0.017799 31.6074 0
32. ## omega -0.31340 0.003263 -96.0543 0
33. ## alpha1 -0.17372 0.012630 -13.7547 0
34. ## beta1 0.96598 0.000036 26838.0412 0
35. ## gamma1 0.18937 0.013003 14.5631 0
36. ## skew 0.84959 0.020089 42.2911 0
37. ## shape 5.99161 0.707324 8.4708 0
38. ##
39. ## LogLikelihood : 10140.27
40. ##
41. ## Information Criteria
42. ## ------------------------------------
43. ##
44. ## Akaike -6.7110
45. ## Bayes -6.6911
46. ## Shibata -6.7110
47. ## Hannan-Quinn -6.7039
48. ##
49. ## Weighted Ljung-Box Test on Standardized Residuals
50. ## ------------------------------------
51. ## statistic p-value
52. ## Lag[1] 0.03028 0.8619
53. ## Lag[2*(p+q)+(p+q)-1][11] 5.69916 0.6822
54. ## Lag[4*(p+q)+(p+q)-1][19] 12.14955 0.1782
55. ## d.o.f=4
56. ## H0 : No serial correlation
57. ##
58. ## Weighted Ljung-Box Test on Standardized Squared Residuals
59. ## ------------------------------------
60. ## statistic p-value
61. ## Lag[1] 1.666 0.1967
62. ## Lag[2*(p+q)+(p+q)-1][5] 2.815 0.4418
63. ## Lag[4*(p+q)+(p+q)-1][9] 3.457 0.6818
64. ## d.o.f=2
65. ##
66. ## Weighted ARCH LM Tests
67. ## ------------------------------------
68. ## Statistic Shape Scale P-Value
69. ## ARCH Lag[3] 0.1796 0.500 2.000 0.6717
70. ## ARCH Lag[5] 1.5392 1.440 1.667 0.5821
71. ## ARCH Lag[7] 1.6381 2.315 1.543 0.7933
72. ##
73. ## Nyblom stability test
74. ## ------------------------------------
75. ## Joint Statistic: 4.4743
76. ## Individual Statistics:
77. ## ar1 0.07045
78. ## ar2 0.37070
79. ## ma1 0.07702
80. ## ma2 0.39283
81. ## omega 1.00123
82. ## alpha1 0.49520
83. ## beta1 0.79702
84. ## gamma1 0.51601
85. ## skew 0.07163
86. ## shape 0.55625
87. ##
88. ## Asymptotic Critical Values (10% 5% 1%)
89. ## Joint Statistic: 2.29 2.54 3.05
90. ## Individual Statistic: 0.35 0.47 0.75
91. ##
92. ## Sign Bias Test
93. ## ------------------------------------
94. ## t-value prob sig
95. ## Sign Bias 0.4723 0.63677
96. ## Negative Sign Bias 1.7969 0.07246 *
97. ## Positive Sign Bias 2.0114 0.04438 **
98. ## Joint Effect 7.7269 0.05201 *
99. ##
100. ##
101. ## Adjusted Pearson Goodness-of-Fit Test:
102. ## ------------------------------------
103. ## group statistic p-value(g-1)
104. ## 1 20 46.18 0.0004673
105. ## 2 30 47.73 0.0156837
106. ## 3 40 67.07 0.0034331
107. ## 4 50 65.51 0.0574582
108. ##
109. ##
110. ## Elapsed time : 0.93679
所有系数均具有统计学意义。在标准化残差或标准化平方残差内未发现相关性。模型正确捕获所有ARCH效果。然而：

*对于某些模型参数，Nyblom稳定性检验无效假设认为模型参数随时间是恒定的

*正偏差为零的假设在5％的显着性水平上被拒绝；这种检验着重于正面冲击的影响

*拒绝了标准化残差的经验和理论分布相同的Pearson拟合优度检验原假设

注意：ARMA（1,2）+ eGARCH（1,1）拟合还提供统计上显着的系数，标准化残差内没有相关性，标准化平方残差内没有相关性，并且正确捕获了所有ARCH效应。但是，偏差检验在5％时不如ARMA（2,2）+ eGARCH（1,1）模型令人满意。

进一步显示诊断图。

我们用平均模型拟合（红线）和条件波动率（蓝线）显示了原始的对数收益时间序列。
2. p <- addSeries(mean_model_fit, col = 'red', on = 1)
3. p <- addSeries(cond_volatility, col = 'blue', on = 1)
4. p
模型方程式

结合ARMA（2,2）和eGARCH模型，我们可以：

yt − ϕ1yt−1 − ϕ2yt−2 = ϕ0 + ut + θ1ut−1 +θ2ut-2ut= σtϵt，ϵt = N（0,1）ln⁡（σt2）=ω+ ∑j = 1q（αjϵt−j2 +γ （ϵt−j–E | ϵt−j |））+ ∑i =1pβiln（σt−12）

使用模型结果系数，结果如下。

yt +0.476 yt-1 +0.575 yt-2 = ut +0.429 ut-1 +0.563 ut-2ut = σtϵt，ϵt = N（0,1）ln⁡（σt2）= -0.313 -0.174ϵt-12 +0.189（ ϵt−1–E | ϵt−1 |））+ 0.966 ln（σt−12）

波动率分析

这是由ARMA（2,2）+ eGARCH（1,1）模型得出的条件波动图。
```
plot(cond_volatility)
```
显示了年条件波动率的线线图。
2. pl <- lapply(2007:2018, function(x) { plot(cond_volatility[as.character(x)])
3. pl
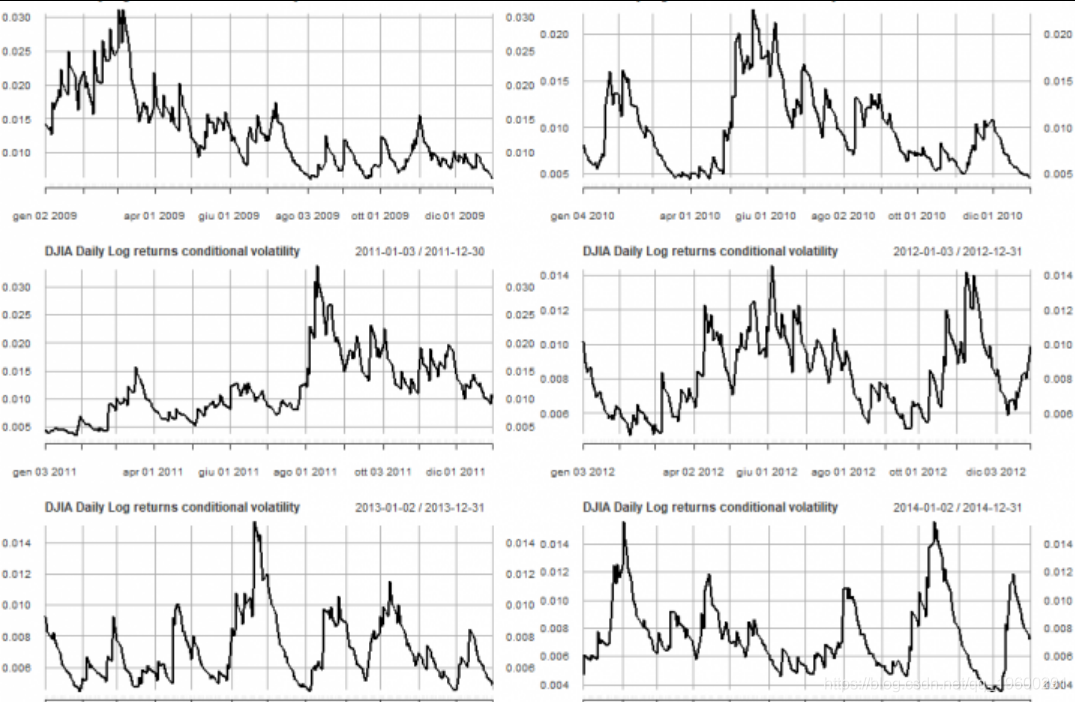
显示了按年列出的条件波动率箱图。

2008年之后，日波动率基本趋于下降。在2017年，波动率低于其他任何年。不同的是，与2017年相比，我们在2018年的波动性显着增加。

最受欢迎的见解

1.HAR-RV-J与递归神经网络（RNN）混合模型预测和交易大型股票指数的高频波动率

2.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长

3.波动率的实现：ARCH模型与HAR-RV模型

4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测

5.GARCH（1,1），MA以及历史模拟法的VaR比较

6.R语言多元COPULA GARCH 模型时间序列预测

7.R语言基于ARMA-GARCH过程的VAR拟合和预测

8.matlab预测ARMA-GARCH 条件均值和方差模型

9.R语言对S＆P500股票指数进行ARIMA + GARCH交易策略
▍关注我们【大数据部落】第三方数据服务提供商,提供全面的统计分析与数据挖掘咨询服务,为客户定制个性化的数据解决方案与行业报告等。 ▍咨询链接：http://y0.cn/teradat ▍联系邮箱：3025393450@qq.com
查看全文

相关阅读:
单核时代，PHP之类多线程或者多进程的，是怎么处理并发的？是排队吗？
高并发下的Node.js与负载均衡
 telnet 查看端口是否可访问
 同步与异步--
函数式编程沉思录(草稿)
面向状态机编程
 promise是有状态的moand
异步链式编程—promise沉思录
 同步与异步
 网络编程释疑之：同步，异步，阻塞，非阻塞

原文地址：https://www.cnblogs.com/tecdat/p/14396941.html

Copyright © 2011-2022 走看看