原文链接:http://tecdat.cn/?p=22838
原文出处:拓端数据部落公众号
问题:使用R中的鸢尾花数据集
(a)部分:k-means聚类
使用k-means聚类法将数据集聚成2组。
画一个图来显示聚类的情况
使用k-means聚类法将数据集聚成3组。
画一个图来显示聚类的情况
(b)部分:层次聚类
使用全连接法对观察值进行聚类。
使用平均和单连接对观测值进行聚类。
绘制上述聚类方法的树状图。
问题01:使用R中建立的鸢尾花数据集。
(a):k-means聚类
讨论和/或考虑对数据进行标准化。
-
-
data.frame(
-
"平均"=apply(iris[,1:4], 2, mean
-
"标准差"=apply(iris[,1:4], 2, sd)
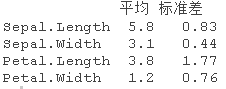
在这种情况下,我们将标准化数据,因为花瓣的宽度比其他所有的测量值小得多。
使用k-means聚类法将数据集聚成2组
使用足够大的nstart,更容易得到对应最小RSS值的模型。
kmean(iris, nstart = 100)画一个图来显示聚类的情况
-
-
# 绘制数据
-
plot(iris, y = Sepal.Length, x = Sepal.Width)
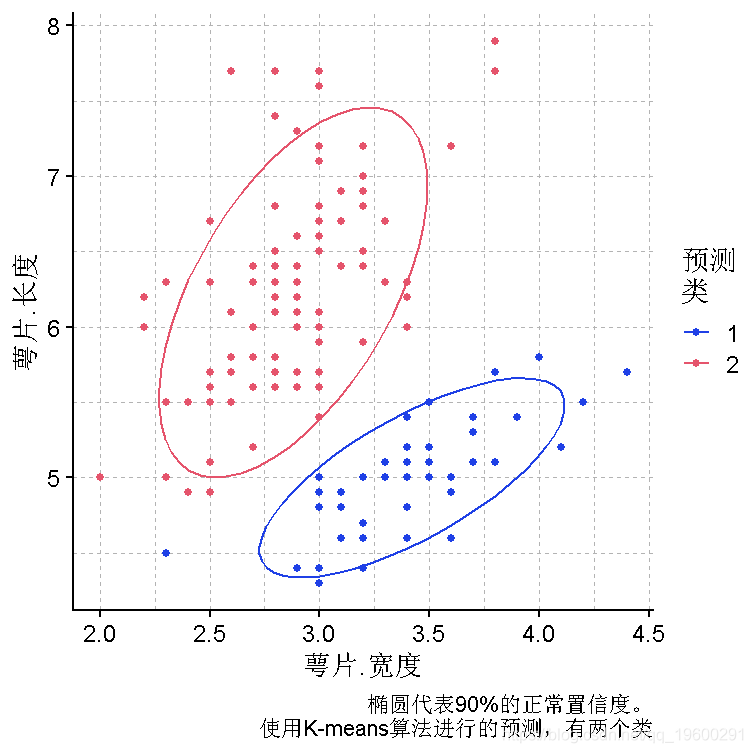
为了更好地考虑花瓣的长度和宽度,使用PCA首先降低维度会更合适。
-
# 创建模型
-
-
PCA.mod<- PCA(x = iris)
-
-
#把预测的组放在最后
-
PCA$Pred <-Pred
-
-
#绘制图表
-
plot(PC, y = PC1, x = PC2, col = Pred)
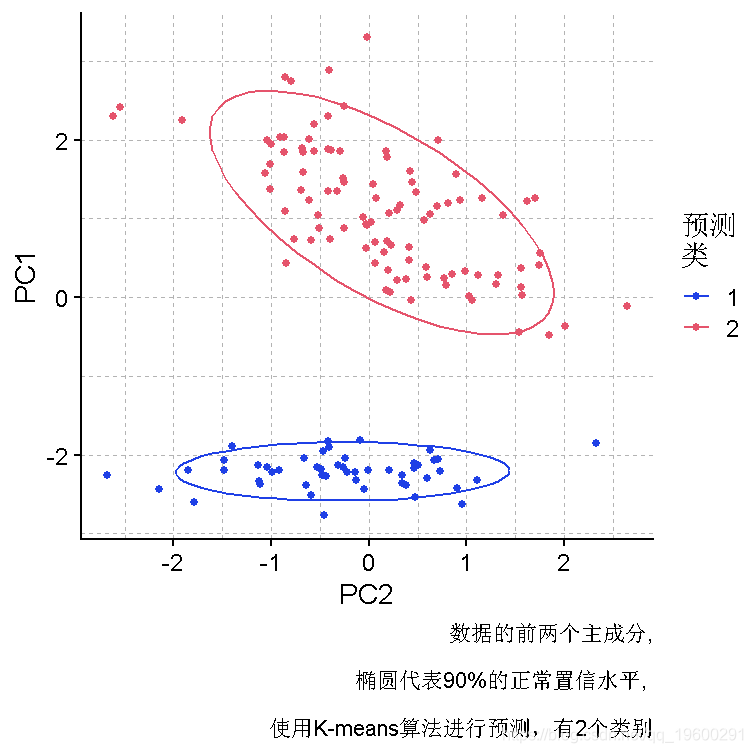
为了更好地解释PCA图,考虑到主成分的方差。
-
## 看一下主要成分所解释的方差
-
-
for (i in 1:nrow) {
-
pca[["PC"]][i] <- paste("PC", i)
-
}
-
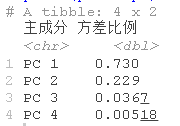
plot(data = pca,x = 主成分, y = 方差比例, group = 1)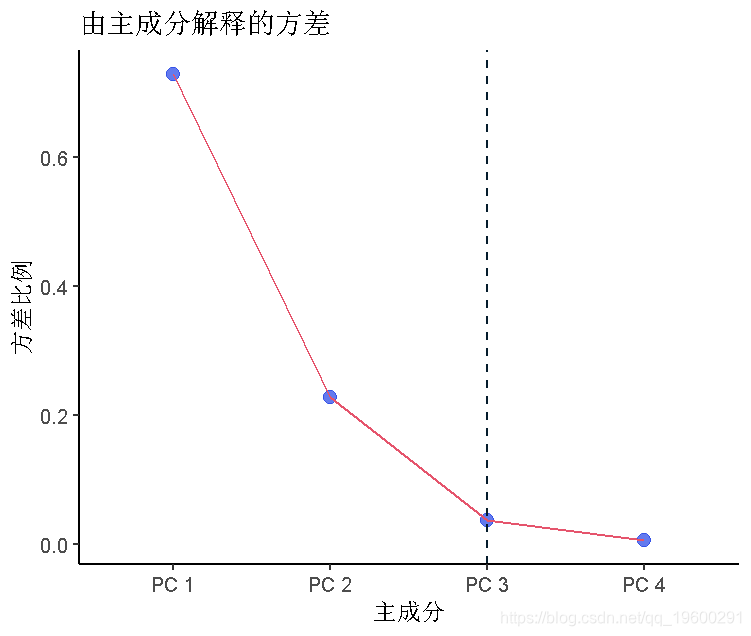
数据中80%的方差是由前两个主成分解释的,所以这是一个相当好的数据可视化。
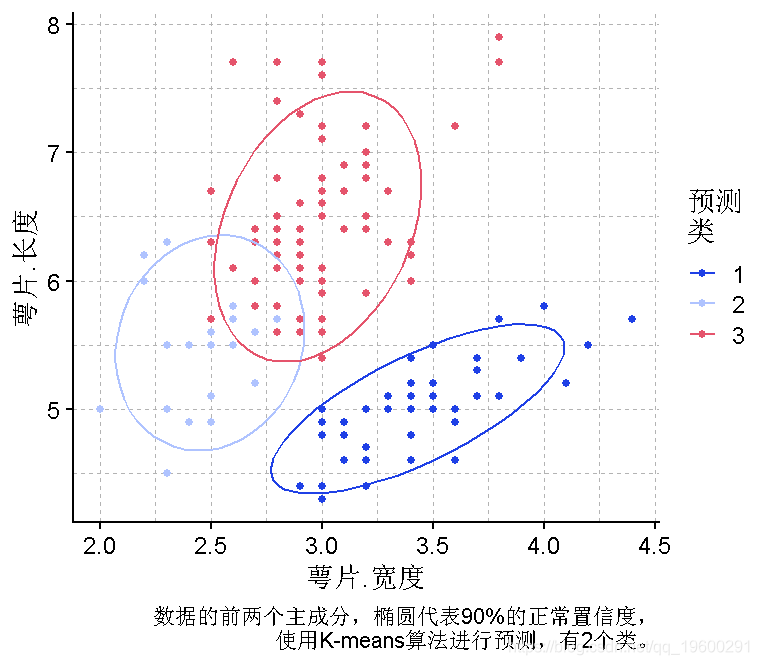
使用k-means聚类法将数据集聚成3组
在之前的主成分图中,聚类看起来非常明显,因为实际上我们知道应该有三个组,我们可以执行三个聚类的模型。
-
kmean(input, centers = 3, nstart = 100)
-
# 制作数据
-
groupPred %>% print()

画一个图来显示聚类的情况
-
-
-
# 绘制数据
-
plot(萼片长度,萼片宽度, col =pred)
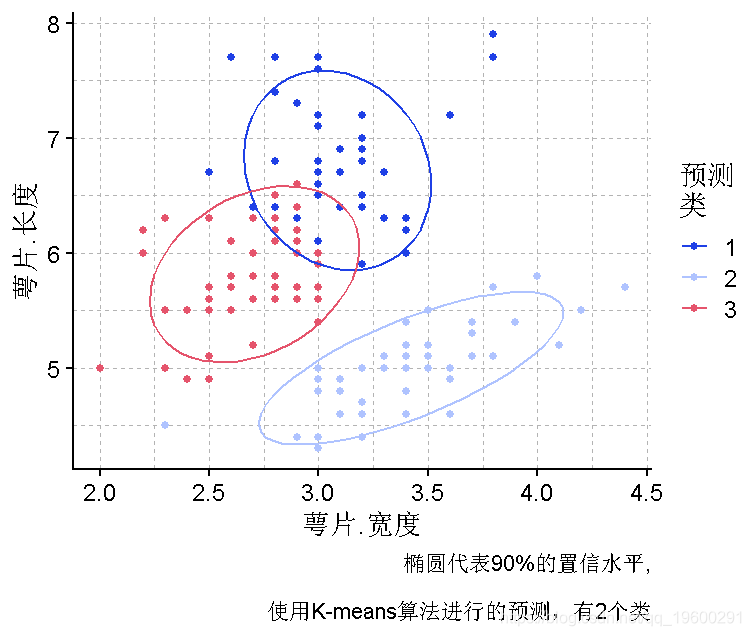
PCA图
为了更好地考虑花瓣的长度和宽度,使用PCA首先减少维度是比较合适的。
-
#创建模型
-
prcomp(x = iris)
-
-
#把预测的组放在最后
-
PCADF$KMeans预测<- Pred
-
-
#绘制图表
-
plot(PCA, y = PC1, x = PC2,col = "预测 聚类", caption = "鸢尾花数据的前两个主成分,椭圆代表90%的正常置信度,使用K-means算法对2个类进行预测") +
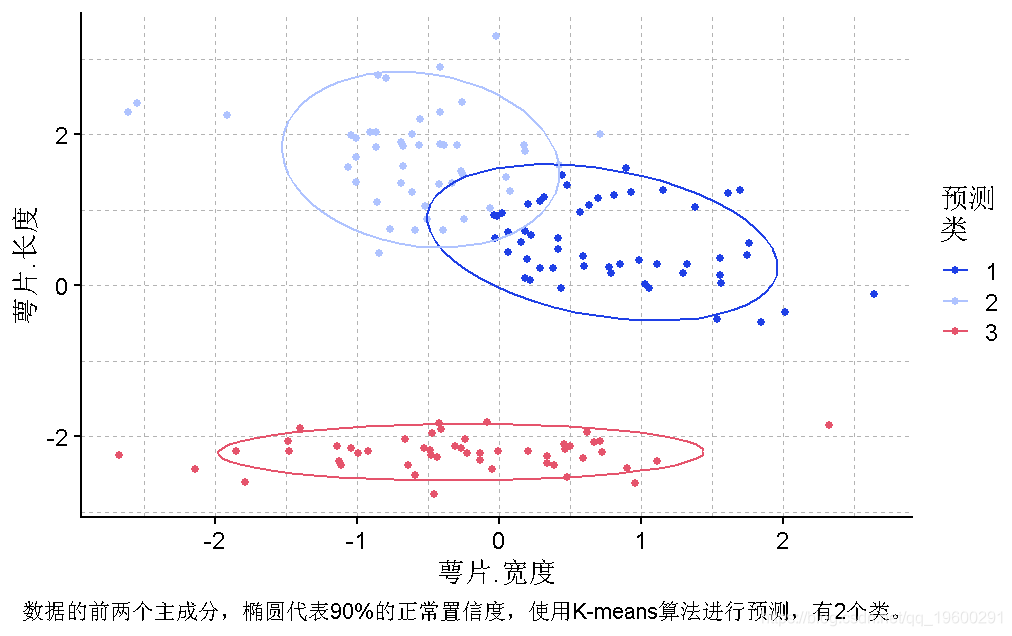
PCA双曲线图
萼片长度~萼片宽度图的分离度很合理,为了选择在X、Y上使用哪些变量,我们可以使用双曲线图。
biplot(PCA)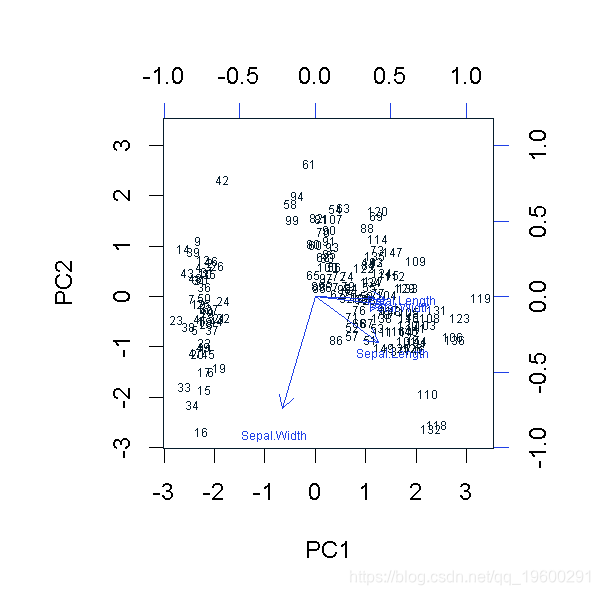
这个双曲线图显示,花瓣长度和萼片宽度可以解释数据中的大部分差异,更合适的图是:
plot(iris, col = KM预测)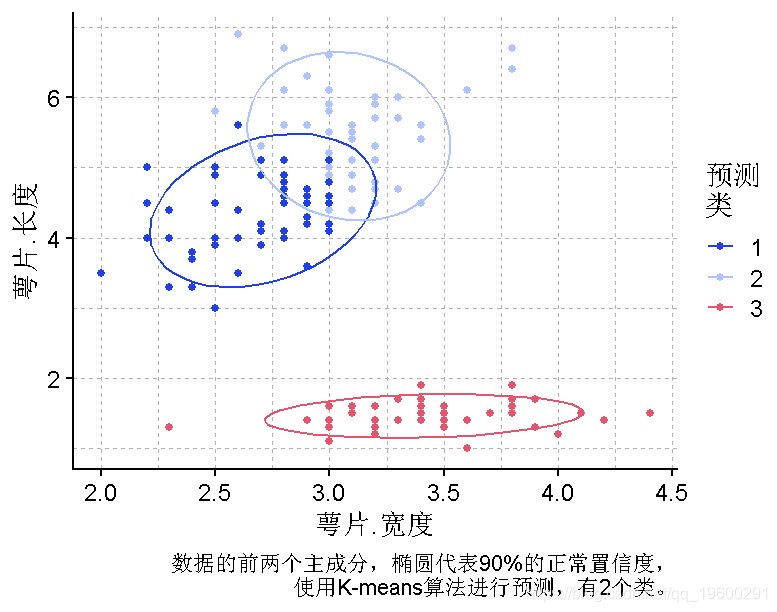
评估所有可能的组合。
-
iris %>%
-
pivot_longer() %>%
-
plot(col = KM预测, facet_grid(name ~ ., scales = 'free_y', space = 'free_y', ) +
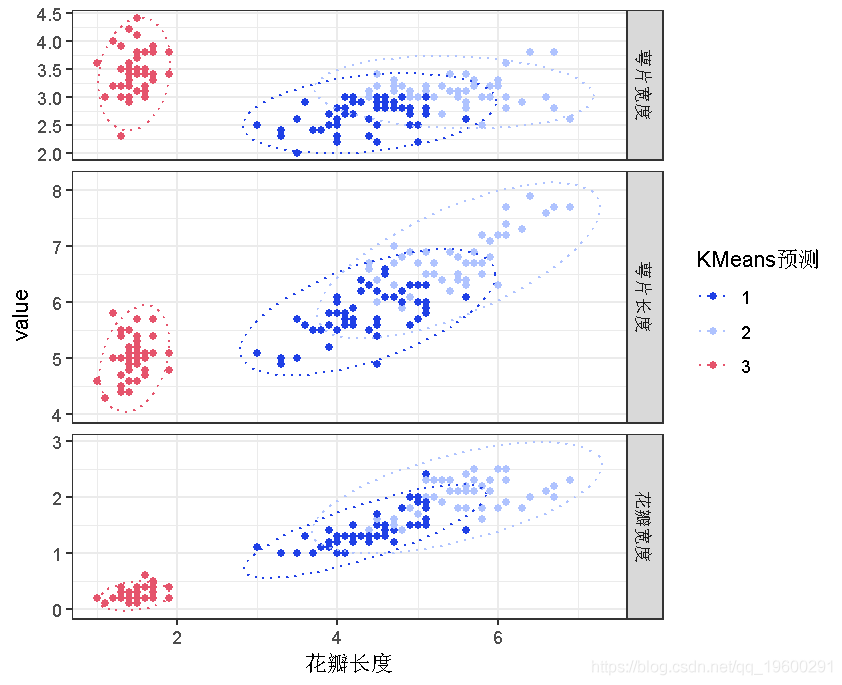
层次聚类
使用全连接法对观测值进行聚类。
可以使用全连接法对观测值进行聚类(注意对数据进行标准化)。
hclust(dst, method = 'complete')使用平均和单连接对观察结果进行聚类。
-
hclust(dst, method = 'average')
-
hclust(dst, method = 'single')
绘制预测图
现在模型已经建立,通过指定所需的组数,对树状图切断进行划分。
-
-
# 数据
-
iris$KMeans预测<- groupPred
-
-
-
# 绘制数据
-
plot(iris,col = KMeans预测))
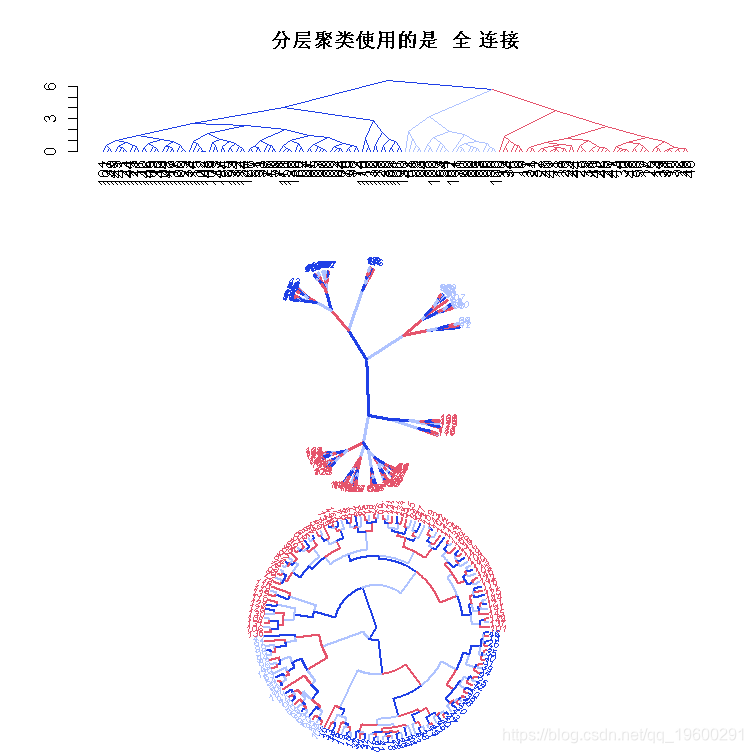
绘制上述聚类方法的树状图
对树状图着色。
-
type<- c("平均", "全", "单")
-
-
for (hc in models) plot(hc, cex = 0.3)
-



最受欢迎的见解
3.R语言对用电负荷时间序列数据进行K-medoids聚类建模和GAM回归
5.Python Monte Carlo K-Means聚类实战