【Binary Space Partitioning】
BSP was discovered by John Carmack used BSP trees in Doom and Quake. Although the game Doom is now of some age virtually all the latest first person shooters still use BSP engines which really goes to show how this technique has stood the test of time.
Performing a for/next loop to sort all your levels polygons every frame would result in a performance level where you could probably bake a cake in between frame updates.
每帧对所有 Polygon 的排序会很卡。
Add to that collision detection of all the polygons in your level (having to check if you have hit each one) and then you could probably ice the cake as well.Not only that
每帧加上 Collision Detection 后会更卡。
对不透明物体,使用Z-Buff即可得正确的渲染结果。但对透明物体,Z-Buff就不管用了。对透明物体来说,不拆分物体,而仅仅依靠次序,是无法得到正确的渲染结果的。

Storing a level in a BSP Tree can provide many benefits in other areas (collision detection,polygon culling).
Not only can a BSP tree be used for drawing all the polygons in your scene in the right order (WITHOUT the need for a Z-Buffer) but it can also be used (in my opinion more importantly) for culling any unseen objects from the fustrum at lightning speed.
最原始的 BSPNode 结构:

struct BSPNode { POLYGON *splitter; BSPNode *FrontChild; BSPNode *BackChild; };
渲染BSP树:

void RenderBSP (NODE * CurrentNode) { int Result; Result=ClassifyPoint(CameraPosition,CurrentNode->Polygon); if (Result==Front) { if (CurrentNode->BackChild!=NULL) RenderBSP (CurrentNode->BackChild); DrawPolygon(CurrentNode->Polygon); if (CurrentNode->FrontChild!=NULL) RenderBSP (CurrentNode->FrontChild); } else { if (CurrentNode->FrontChild!=NULL) RenderBSP (CurrentNode->FrontChild); DrawPolygon(CurrentNode->Polygon); if (CurrentNode->BackChild!=NULL) RenderBSP (CurrentNode->BackChild); } }
问题来了,如果有多边形完全与 Splitter 重叠,该怎么办?一种实现是,将这些重叠的多边形都加入当前 BSPNode,也即一个 BSPNode 可能包含多个物体。
每一个物体有正反两面,当摄像机在物体背面时,看不见该物体。
WalkBSPTree

void WalkBspTree(NODE *Node,D3DVECTOR *pos) { POLYGON *shared; int result=ClassifyPoint(pos,Node-> Splitter); if (result==CP_FRONT) { shared=Node-> Splitter->SameFacingShared; if (Node-> Back!=NULL) WalkBspTree(Node-> Back,pos); lpDevice-> DrawIndexedPrimitive(D3DPT_TRIANGLELIST,D3DFVF_LVERTEX, &Node-> Splitter-> VertexList[0], Node-> Splitter-> NumberOfVertices, &Node-> Splitter->Indices[0], Node-> Splitter-> NumberOfIndices, NULL); while (shared!=NULL) { lpDevice-> DrawIndexedPrimitive(D3DPT_TRIANGLELIST,D3DFVF_LVERTEX, &shared-> VertexList[0], shared-> NumberOfVertices, &shared-> Indices[0], shared-> NumberOfIndices, NULL); shared=shared-> SameFacingShared; } if (Node->Front!=NULL) WalkBspTree(Node->Front,pos); return ; } // this means we are at back of node shared=Node->Splitter->OppositeFacingShared; if (Node->Front!=NULL) WalkBspTree(Node->Front,pos); while (shared!=NULL) { lpDevice-> DrawIndexedPrimitive(D3DPT_TRIANGLELIST,D3DFVF_LVERTEX,&shared-> VertexList[0],shared-> NumberOfVertices,&shared-> Indices[0],shared-> NumberOfIndices,NULL); shared=shared-> OppositeFacingShared; } if (Node-> Back!=NULL) WalkBspTree(Node->Back,pos); return; }
判定 Point 在 Plane 的 Front or Back:

int ClassifyPoint(D3DVECTOR *pos,POLYGON * Plane) { float result; D3DVECTOR *vec1=(D3DVECTOR *)&Plane-> VertexList[0]; D3DVECTOR Direction=(*vec1)-(*pos); result=DotProduct(Direction,Plane->Normal); if (result< -0.001) return CP_FRONT; if (result> 0.001) return CP_BACK; return CP_ONPLANE; }
判定 Polygon 在 Plane 的 Front or Back:

int ClassifyPoly(POLYGON *Plane,POLYGON * Poly) { int Infront=0; int Behind=0; int OnPlane=0; float result; D3DVECTOR *vec1=(D3DVECTOR *)&Plane->VertexList[0]; for (int a=0;aNumberOfVertices;a++) { D3DVECTOR *vec2=(D3DVECTOR *)&Poly->VertexList[a]; D3DVECTOR Direction=(*vec1)-(*vec2); result=DotProduct(Direction,Plane->Normal); if (result> 0.001) { Behind++; } else if (result< -0.001) { Infront++; } else { OnPlane++; Infront++; Behind++; } } if (OnPlane==Poly-> NumberOfVertices) return CP_FRONT;// this would nomrally be CP_ONPLANE if (Behind==Poly-> NumberOfVertices) return CP_BACK; if (Infront==Poly-> NumberOfVertices) return CP_FRONT; return CP_SPANNING; }
LineOfSight:


bool LineOfSight (D3DVECTOR *Start,D3DVECTOR *End, NODE *Node) { float temp; D3DVECTOR intersection; if (Node->IsLeaf==true) { return !Node->IsSolid; } int PointA=ClassifyPoint(Start,Node->Splitter); int PointB=ClassifyPoint(End,Node->Splitter); if (PointA==CP_ONPLANE && PointB==CP_ONPLANE) { return LineOfSight(Start,End,Node->Front); } if (PointA==CP_FRONT && PointB==CP_BACK) { Get_Intersect (Start,End,(D3DVECTOR *) &Node->Splitter->VertexList[0],&Node->Splitter->Normal,&intersection,&temp); return LineOfSight(Start,&intersection,Node->Front) && LineOfSight(End,&intersection,Node->Back) ; } if (PointA==CP_BACK && PointB==CP_FRONT) { Get_Intersect (Start,End,(D3DVECTOR *) &Node->Splitter->VertexList[0],&Node->Splitter->Normal,&intersection,&temp); return LineOfSight(End,&intersection,Node->Front) && LineOfSight(Start,&intersection,Node->Back) ; } // if we get here one of the points is on the plane if (PointA==CP_FRONT || PointB==CP_FRONT) { return LineOfSight(Start,End,Node->Front); } else { return LineOfSight(Start,End,Node->Back); } return true; }
【Leaf BSP Tree】
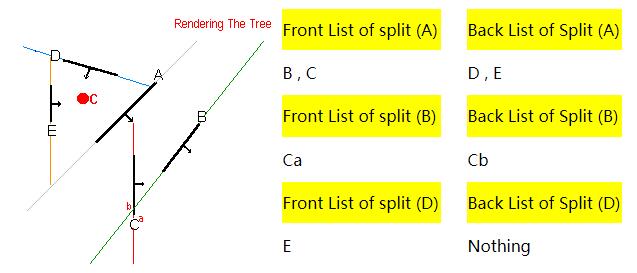
1、First we choose a splitter from the Polygon List as we did before BUT instead of storing the polygon itself at the Node we only store the polygons Plane.
每个Node只存储 Polygon Plane.
2、The polygon is marked as having been used as a splitter but unlike the Node based compiler we do NOT remove the polygon from the list.We send it down its own front list and this polygon may still continue to be split by other Polygons Planes.
Polygonp被标记为已选中。不删除 polygon,只是加入到 FrontList中。可以被后续的Splitter分割。
3、If a polygon that has already been used as a Plane is split into two further down the tree then the polygon is removed as before and two new polygons are created but it is very important to realise that these splits inherit whether or not they have been used as a splitter from the parent.
被分割后的子Polygon,继承父Polygon的选中状态。
4、we check the Front list and the Back list and if all the polygons in any of the lists are ALL infront of one another then this list forms a convex hull and no longer has to be subdivided because if they are all in front of one another then none of them can be intersecting each other.This List (Front or Back) then becomes a Leaf.
每一个都在其它的正面。

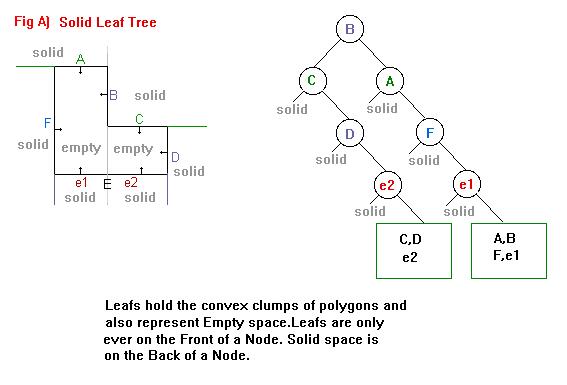
【Solid Leaf BSPTree】
1、A polygon is selected from the list and a Plane is created using the polygon info and stored in the newly created Node.This Plane is now the splitter for the current Node.We also mark the polygon that was selected and from which the Plane was created from as having been used as a splitter already so that it can not get choosen again.
选择 Polygon,根据 Polygon创建一个 Plane作为splitter,标记 Polygon 为选过状态。
2、loop though every polygon in the list (including the one that was used as the splitter) classify the polygon against the splitting Plane.
迭代当前 Polygon 在内的所有 Polygon。
Just as before if the Polygon is Behind the plane it gets added to the Back List and if it is in front of the plane it gets added to the Front List.If the polygon is ON (sharing) the plane then the Normal of the polygon is compared to the Normal split Plane.If the Polygons Normal is facing the same way as the Split Plane then the polygon is added to the Front List.If the Polygon Normal is facing in the opposite direction to the Split Plane then the polygon is added to the back list.
将所有的Pologon放入 Front、Back Listk中。On Plane Polygon 根据法线方向来判定。
3、 We check each Polygon in the Front list and if ALL the polygons have already been used as a Split Plane then this is a Convex Leaf and the polygons can be written to a leaf structure and attached to the current Nodes front.
当 Front List 中所有的 Polygon 都被选中过(即每一个都在每一个的前面),则形成了凸包,则将这些 Polygon 加入到一个Leaf中,这个Leaf叫 Convex Leaf。
4、We will see this in action in a moment.We now check the back list,if there are NO polygons left in the back list then we simply store a -1 in the Nodes Back Pointer.This means if we ever try to go down the back of this node we will know that the -1 means we can not because it is solid space.I
当Back 无物体时,Back List 存储为-1。
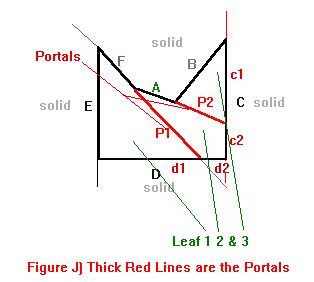
【Portal】
These portals will not be rendered or even kept after the PVS has been calculated but they are needed because if we can create a Portal to plug up the doorway then getting the dimensions of this Portal will get us the dimensions of the doorway which is exactly what we need.
As you can probably imagine creating portal Polygons to fit into all the gaps in our level is going to create many many portals.In otherwords if a room has 5 doorways we will need create a portal in each doorway and so on for every leaf .
Because of the nature of BSP trees portals between two leafs will always be on one of the Split planes in out tree.Above Portal 1 is on Node F's split plane and Portal 2 is on Node A's split plane.
【Anti-Penumbra】
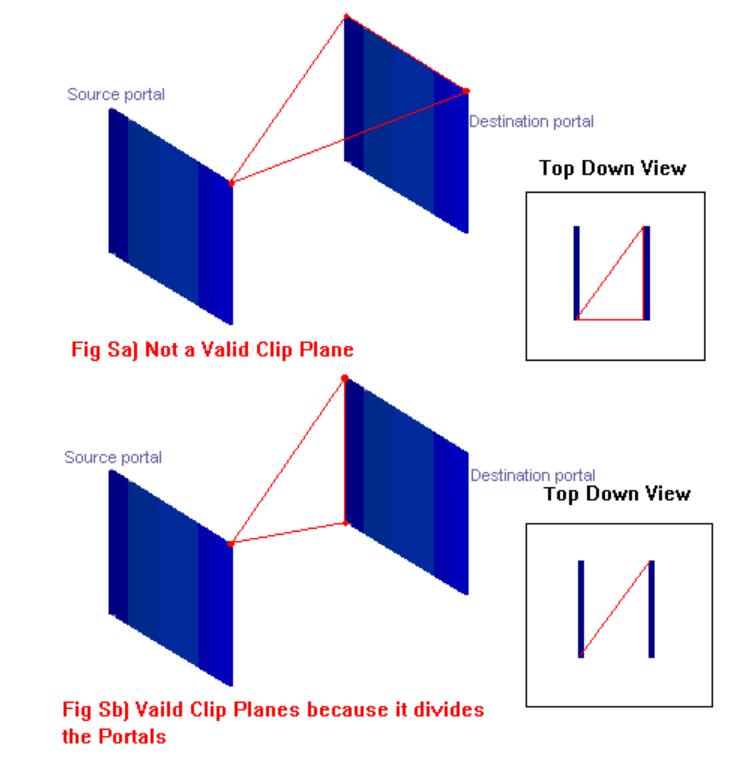
walk through each leaf in the tree and for every portal in that leaf create an ANTI-PENUMBRA between that Portal and every Portal in the Leafs adjoining that leaf and so on.

A Plane is considered to be an Anti-Penumbra plane if the plane clearly divides the Source Portal and the Destination portal.That is to say the Plane is accepted if the Source Portal lays of one side of the Plane and the Destination portal lays on the other.
参考:
1、https://www.cs.utah.edu/~jsnider/SeniorProj/BSP1/default.html
2、https://www.cs.utah.edu/~jsnider/SeniorProj/BSP/default.htm
