网络流(二)----最大流Dinic算法

以 HDU 4183  Pahom on Water 为例的 模板代码

#include <cstdio>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <map>

using namespace std;

const int inf = 0x3f;
const int INF = 0x3f3f3f3f;
const int maxn = 40002;

struct Node
{
    int to, flow, next;
}edge[maxn * 8];

int n, m;
int S, T, tot;
int q[maxn];
int dis[maxn]; //记录层次
int pre[maxn], rec[maxn], head[maxn];
bool block[maxn];

inline void Add_edge(int a, int b, int c)
{
    edge[tot].to = b; edge[tot].flow = c; edge[tot].next = head[a];
    head[a] = tot++;
    edge[tot].to = a; edge[tot].flow = 0; edge[tot].next = head[b];
    head[b] = tot++;
}

void Init()
{
    tot = 0; 
    memset(head, -1, sizeof(head));
}

void BFS()
{
    int i;
    int h = 0, t = 0;
    memset(dis, INF, sizeof(dis));
    q[h] = S;
    dis[S] = 0;
    while(h <= t)
    {
        int u = q[h++];
        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            int v = edge[i].to;
            if(dis[v] == INF && edge[i].flow)
            {
                dis[v] = dis[u] + 1;
                q[++t] = v;
            }
        }
    }
}

int Dinic()
{
    int i, j;
    int top = S, MaxFlow = 0, mins = INF;
    pre[S] = S;
    BFS();
    memset(block, 0, sizeof(block));
    while(dis[T] != INF)
    {
        for(i = head[top]; i != -1; i = edge[i].next)
        {
            if(edge[i].flow && dis[top]+1 == dis[edge[i].to] && !block[edge[i].to])
                break;
        }
        if (i != -1)
        {
            j = edge[i].to;
            mins = min(mins, edge[i].flow);
            pre[j] = top;
            rec[j] = i;
            top = j;
            if(top == T)
            {
                i = -1;
                MaxFlow += mins;
                for(; top != S; top = pre[top])
                {
                    edge[rec[top]].flow -= mins;
                    edge[rec[top]^1].flow += mins;
                    if(!edge[rec[top]].flow) 
                    {
                        i = top;
                    }
                }
                if(i != -1)
                {
                    i = pre[i];
                    mins = INF;
                    for(j = i; j != S; j = pre[j])
                    {
                        mins = min(mins, edge[rec[j]].flow);
                    }
                    top = i;
                }
            }
        }
        else
        {
            block[top] = true;
            top = pre[top];
            if(block[S])
            {
                BFS();
                memset(block, 0, sizeof(block));
            }
        }
    }
    return MaxFlow;
}

struct Pad
{
    double x, y, rad;
    double fre;
}pad[maxn];

bool cmp(Pad A, Pad B)
{
    return A.fre < B.fre;
}

int main()
{
    int test, a, b;
    scanf("%d", &test);
    while(test--)
    {
        Init();
        scanf("%d", &n);
        for(int i = 1; i <= n; i++)
        {
            scanf("%lf %lf %lf %lf", &pad[i].fre, &pad[i].x, &pad[i].y, &pad[i].rad);
        }
        sort(pad+1, pad+n+1, cmp);

        for(int i = 1; i <= n; i++)
        {
            //printf("%d-->%lf %lf %lf %lf
", i, pad[i].fre, pad[i].x, pad[i].y, pad[i].rad);
            for(int j = i + 1; j <= n; j++)
            {
                if((pad[j].x-pad[i].x) * (pad[j].x-pad[i].x) + (pad[j].y-pad[i].y) * (pad[j].y-pad[i].y)
                        < (pad[i].rad + pad[j].rad) * (pad[i].rad + pad[j].rad))
                {
                    Add_edge(i, j, 1);
                }
            }
        }
        S = 1; T = n;
        a = Dinic();
        Init();
        for(int i = n; i >= 1; i--)
        {
            for(int j = i - 1; j >= 1; j--)
            {
                if((pad[j].x-pad[i].x) * (pad[j].x-pad[i].x) + (pad[j].y-pad[i].y) * (pad[j].y-pad[i].y)
                        < (pad[i].rad + pad[j].rad) * (pad[i].rad + pad[j].rad))
                {
                    Add_edge(i, j, 1);
                }
            }
        }
        S = n; T= 1;
        b = Dinic();
        if(a>1 && b>1) puts("Game is VALID");
        else puts("Game is NOT VALID");
    }
    return 0;
}

下面对Dinic算法的分析

Dinic:

Dinic算法实质是Edmonds-Karp算法的改进。回想下，在Edmonds-Karp算法中，每次利用BFS找出最短（经过的节点数最少）的增广路，然后进行增广，并修改残留网络。

如何改进？

假如我们能预知哪些路径不是最短的，那么每次寻找增广路的时候不就一定能走最短的那些吗？

如何预知？

当然就是预处理，在寻找增广路之前，我们可以从源点出发：做一次BFS，那么很容易就计算出了每个顶点到源点的距离（经过的节点数）。所以层次图就相当于是一个已经预处理好的增广路标志图。然后在层次图的基础上进行增广，直到无法找到增广路。然后在新的残留网络下重新计算出层次图，继续增广，直到某次计算层次图时，源点已经无法到达汇点，算法结束，此时便已找到了最大流。
 

在进一步介绍dinic算法的具体实现和优化前，必须先理解几个名词：

1顶点的层次

在残留网络中，我们把从源点到点的最短路径长度称作点的层次，记为。源点的层次为0。在下面这张残留网络中：

　　

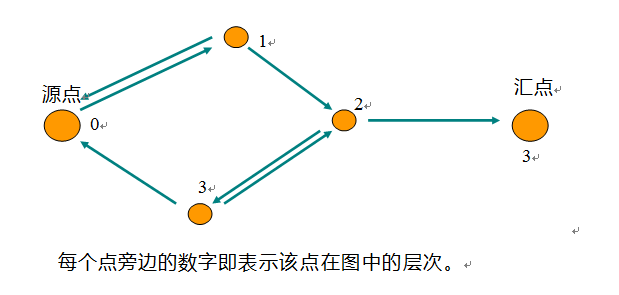
2层次图的概念

    我们这样定义层次图：对于剩余图中的一条边，当且仅当时，边；

直观地讲，层次图是建立在剩余图（残留网络）基础之上的一张“最短路图”。从源点开始，在层次图中沿着边不管怎么走，经过的路径一定是终点在剩余图中的最短路。

3阻塞流的概念

在流量网络中存在一可行流，当该网络的层次图中不存在增广路时，我们称流函数为层次图的阻塞流。

 

4阻塞点的概念

  当从残留网络中节点i出发，无法到达i的下一层次的节点时，已经不可能存在经过i的最短增广路了，即i已经被阻塞了，此时称节点i为阻塞点。显然寻路过程中寻找的节点必须是非阻塞点。

 

Dinic 算法流程如下：

    1) 计算残留网络的层次图。我们定义 dis 为顶点 i 距离源 S 所经过到最少节点数，求出所有顶点的 dis 值，dis[] 值相同的顶点属于同一层，这就是网络的层次图。

2) 在层次图上进行 BFS(或用DFS) 增广，直到不存在增广路径。这时求得的增广路径上顶点是分层的，路径上不可能存在两个顶点属于同一层，即 dis[i]== dis[j] (i ≠ j )。同时，求得层次图后，我们可以在层次图上进行多次增广。

3) 重复 1 和 2。直到层次图中源点已经无法到达汇点，即已不存在增广路。

 

优化：

多路增广:注意到，每次BFS(或DFS)完成后，会找到路径中容量最小的一条边。在这条边之前的路径的容量是大于等于这条边的容量的。那么从这条边之前的点，可能引发出别的增广路径。
比如说 S -> b -> c -> d -> T 是一条增广路径，容量最小的边是 b -> c。
可能存在一条 S -> b -> e -> f -> g -> T 这样的增广路径。
这样的话，在找到第一条增广路径后，只需要回溯到 b 点，就可以继续找下去了。
这样做的好处是，避免了找到一条路径就从头开始寻找另外一条的开销。也就是再次从 S 寻找到 b 的开销。

同时，在同一次的BFS( 或DFS) 中。如果判断出一个点是阻塞点，就将这个点在层次图中抹去。

文章最开始即为Dinic算法的实现.

转载自YB