首先看一看判断素数的方法,就是看一个数n能否被2~n-1内的数整除,如果能整除就不是素数,反之则是,直接上优化后的代码:
1 bool isprime(int x) 2 { 3 for(int i=2;i<=sqrt(x);i++) 4 { 5 if(x%i==0) 6 return false; 7 } 8 return true; 9 }
对于一些题目,需要判断的素数非常大且多,用这种方法的话时间复杂度是绝不允许的,因此就有了素数筛法,顾名思义,是提前把素数筛选出来,这样之后判断的时候就快了。
先说一下素数筛法的原理:
从第一个素数2开始,将所有2的倍数筛掉,因为2的倍数一定不是素数,然后往后,3的倍数筛掉.....一直到只有素数剩下,如图,黄色的数为素数(图片来源于网络)
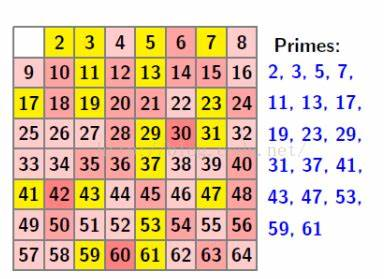
这种筛法有两种算法:
一是Eratosthenes(埃拉托斯特尼)筛法,这个筛法是直接把原理应用上了,从第一个素数开始,只要是自身倍数的,全都检查一遍并筛掉。
代码如下:primelist[ ]代表素数表,isprime[ ]代表是否是素数。
1 bool isprime[maxn+5]; 2 void MakePrimeList() 3 { 4 int cnt=1; 5 memset(isprime,true,sizeof(isprime));//先假设所有数是素数 6 for(int i=2;i<=maxn;i++)//将所有数遍历 7 { 8 if(isprime[i])//判断是否素数 9 primelist[++cnt]=i;//是的话加入素数表 10 for(int j=i+i;j<=maxn;j+=i)//从这个数的最小的倍数开始 11 { 12 isprime[j]=false;//标记为非素数 13 } 14 // for(j=2;j*i<=maxn;j++)这是原型,上面是改进的 15 // { 16 // isprime[i*j]=false; 17 // } 18 } 19 return ; 20 }
这种埃氏筛法时间复杂度氏O(nlognlogn),显然时间复杂度仍然较大。
二是Euler(欧拉)筛法,埃氏筛法复杂度高的原因是很多数都被重复筛了好几次甚至很多次,做了很多不必要的工作,而欧拉筛法就避免了重复筛数。
先看代码:
1 void MakePrimeList() 2 { 3 int cnt=0; 4 memset(isprime,true,sizeof(isprime));//先假设所有数是素数 5 for(int i=2;i<=maxn;i++)//将所有数遍历 6 { 7 if(isprime[i])//判断是否素数 8 primelist[++cnt]=i;//是的话加入素数表 9 for(int j=1;j<=cnt;j++)//这里是从素数表的已知是素数的第一个数开始,到已知数目结束 10 { 11 if(i*primelist[j]>maxn) 12 break; 13 isprime[i*primelist[j]]=false;//这样循环下去,就把所有非素数找到并标记了 14 if(i%primelist[j]==0)//这里和关于j的for循环是关键,保证不重复筛数 15 break; 16 } 17 } 18 return ; 19 }
百度上关于if(i%primelist[j]==0)有这样解释:(这里prime[]相当于primelist[])
prime[]数组中的素数是递增的,当i能整除prime[j],那么i*prime[j+1]这个合数肯定被prime[j]乘以某个数筛掉。
因为i中含有prime[j],prime[j]比prime[j+1]小,即i=k*prime[j],那么i*prime[j+1]=(k*prime[j])*prime
[j+1]=k’*prime[j],接下去的素数同理。所以不用筛下去了。因此,在满足i%prime[j]==0这个条件之前以及第一次
满足改条件时,prime[j]必定是prime[j]*i的最小因子。
举个例子:从第一个素数2开始,此时 i 等于2,i*2=4(始终是从j=1即第一个素数开始乘以 i,下同),4不是素数,标记,i%2==0,停止。i++;
第二个数也是第二个素数3,此时 i 等于3,i*2=6,6被标记不是素数,i%2!=0,i*3=9,9被标记,i%3==0,停止。i++;
第三个数4不是素数,不加入表, 此时 i 等于4,i*2=8,8被标记,i%2==0,停止,i++;
.......等等..
它始终是把离当前素数最近的数筛掉,而且不重不漏,时间复杂度是o(n),确实被证明过是O(n)。
例题:lightoj1259 - Goldbach`s Conjecture
题意就是给你一个数,让你把它拆成两个素数数相加,问有多少种方法(a<b就是不能重复)
直接在素数表中找判断即可。
代码如下:
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 using namespace std; 6 const int maxn=10000000; 7 int primelist[maxn/10]; 8 bool isprime[maxn+5]; 9 void MakePrimeList() 10 { 11 int cnt=0; 12 memset(isprime,true,sizeof(isprime)); 13 for(int i=2;i<=maxn;i++) 14 { 15 if(isprime[i]) 16 primelist[++cnt]=i; 17 for(int j=1;j<=cnt;j++) 18 { 19 if(i*primelist[j]>maxn) 20 break; 21 isprime[i*primelist[j]]=false; 22 if(i%primelist[j]==0) 23 break; 24 } 25 } 26 return ; 27 } 28 int main() 29 { 30 int n,t; 31 int cas=0; 32 cin>>t; 33 MakePrimeList(); 34 while(t--) 35 { 36 int num=0,cnt=1; 37 scanf("%d",&n); 38 for(int i=1;primelist[i]<=n/2;i++)//从素数表中第一个数到大小为n/2是因为a<b 39 { 40 if(isprime[n-primelist[i]]) 41 num++; 42 } 43 printf("Case %d: %d ",++cas,num); 44 } 45 return 0; 46 }