唯一分解定理又称为算数基本定理，基本内容是：
每个大于1的自然数，要么本身就是质数，要么可以写为2个或以上的质数的积，而且这些质因子按大小排列之后，写法仅有一种方式。
用另一种方法表示就是：
对于任何一个大于1的正整数,都存在一个标准的分解式: N=p1^a1 * p2^a2*···*pn^an;（其中一系列an为指数，pn为质数）
此定理表明：任何一个大于 1 的正整数都可以表示为素数的积。
有这样几个式子：
设F(n)代表n的正因子的数量，则F(n)=(a1+1)*(a2+1)*(a3+1)*······*(an+1)；
设G(n)代表n的正因子的和，则G(n)=(1+p1^2+p1^3+...+p1^a1)*(1+p2^2+p2^3+...p2^a2)*....*(1+pn^1+pn^2+...+pn^an)=
；
获得一个数正因子数量的代码：
primel [ ]是素数表
1 ll getfac(ll x) 2 { 3 ll ans=1; 4 for(int i=1;i<=cnt&&primel[i]<=x;i++) 5 { 6 ll sum=0;//当前质因数的幂指数 7 while(x%primel[i]==0)//当是这个数的因子时 8 { 9 sum++; 10 x/=primel[i]; 11 } 12 ans*=(sum+1);//应用定理的结论 13 } 14 if(x>1)//当搜索不到的时候，如果这个数最后大于一，那么这个最后结果肯定是素数，并且指数是1 15 ans*=2; 16 return ans; 17 }
来看一个应用此定理的例题：
链接：Light OJ 1341 Aladdin and the Flying Carpet
此题的题意就是，给定一个矩形（非正方形）的面积 a，求可以分解的长*宽有多少组，且任意一条边不能小于b，不能重复（4*3和3*4重复）。
即求一个数可以分解为多少个正因数相乘，想到唯一分解定理，用它把所有可能的因子找出后，再除以2，在把小于b的因子暴力去除。
看代码：
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 typedef long long ll; 6 const int maxn=1e6+20; 7 int primel[maxn]; 8 bool isp[maxn]; 9 int cnt; 10 void makel()//欧拉筛打印素数表 11 { 12 cnt=0; 13 memset(isp,true,sizeof(isp)); 14 for(int i=2;i<maxn;i++) 15 { 16 if(isp[i]) 17 primel[++cnt]=i; 18 for(int j=1;j<=cnt;j++) 19 { 20 if(i*primel[j]>maxn) 21 break; 22 isp[i*primel[j]]=false; 23 if(i%primel[j]==0) 24 break; 25 } 26 } 27 } 28 ll getfac(ll x)//唯一分解定理 29 { 30 ll ans=1; 31 for(int i=1;i<=cnt&&primel[i]*primel[i]<=x;i++) 32 { 33 ll sum=0; 34 while(x%primel[i]==0) 35 { 36 sum++; 37 x/=primel[i]; 38 } 39 ans*=(sum+1); 40 } 41 if(x>1) 42 ans*=2; 43 return ans; 44 } 45 int main() 46 { 47 int t; 48 int cas=0; 49 ll a,b; 50 cin>>t; 51 makel(); 52 while(t--) 53 { 54 scanf("%lld%lld",&a,&b); 55 if(a<b*b)//不可能分解为比b大的数相乘 56 { 57 printf("Case %d: 0 ",++cas); 58 continue; 59 } 60 ll count=getfac(a)/2;//不能重复 61 for(int i=1;i<b;i++)//去除小于b的因子 62 { 63 if(a%i==0) 64 count--; 65 } 66 printf("Case %d: %lld ",++cas,count); 67 } 68 return 0; 69 }
再看一个题：
这个题运用了分解质因子和的公式（原理）。
链接：LightOJ 1136 Sigma Function
这个题其实就是求1~n所有的数中，可分解为质因子的和为偶数的数有多少个。
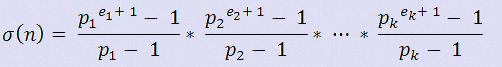这个其实就是那个和的公式（结论）。
把上面的结论搬下来，那个公式G(n)=(1+p1^2+p1^3+...+p1^a1)*(1+p2^2+p2^3+...p2^a2)*....*(1+pn^1+pn^2+...+pn^an)；
就是要让它等于偶数，分析一下，这首先是乘积式，如果要让乘积为偶数，那么每一项就是偶数，可是这样的话pi如果偶数那么所有pi为偶数的G(n)都是奇数（pi^ai一定为偶，再加个1），在剩下的情况中，得分很多情况，定TLE。于是想反面，求多少个G（n）为奇数，再减去。
如果要让和为奇数，想奇*偶=偶，奇*奇=奇，偶*偶=偶，于是只要让每一项（1+pi^ai）为奇数即可，如果p[i] = 2;，则其和一定为奇数（2的幂次和为偶+1），除了2以外，素数都是奇数，所以 （p[i]^0 + p[i]^1 +.....+ p[i]^e[i]）要满足是奇数的话e[i]一定是偶数（首先奇数任何次幂仍为奇数，奇+奇=偶两两组合后一定还剩一个奇数，然后偶+奇=奇），如果 n 是一个平方数，那么他的约数和一定是奇数，如果2*n是平方数，他的约数和也是奇数。
代码如下：
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 using namespace std; 5 typedef long long ll; 6 int main() 7 { 8 int t,cas=0; 9 ll n; 10 cin>>t; 11 while(t--) 12 { 13 scanf("%lld",&n); 14 ll ans; 15 ans=n-(ll)sqrt(n)-(ll)sqrt(n/2); 16 printf("Case %d: %lld ",++cas,ans); 17 } 18 return 0; 19 }