和上面几题差不多的
Euler's Totient function, φ(n) [sometimes called the phi function]:小于等于n的数并且和n是互质的数的个数
存在这样的数:N的欧拉数φ(n),是N的一个排列
例如:φ(87109)=79180
求在1---10^7中n/φ(n) 取到最小的 n 是多少?
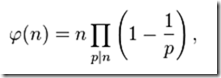
这里的是p是n的素因子,当素因子有相同的时候只取一个
任意一个正整数都能分解成若干个素数乘积的形式
直接利用上题的phi函数就可以求解
这个是跑的最快的函数了
long phi2(long n){ long res = 0; if(n==1) return 0; int pi=2; res = n; while(pi*pi <=n){ if(n%pi==0){ res/=pi; res*=(pi-1); while(n%pi==0){ n/=pi; } } pi++; } if(n>1){ res/=n; res*=(n-1); } return res; } // 8319823 // running time=89s43ms
运行结果也90s了
然后考虑到
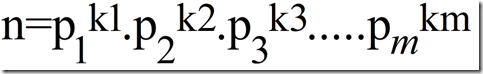
这里的pi都是素数
所以我们可以只考虑素数的情况
当n%pi==0的时候这个pi就符合条件,并去重
void run2(){ long Max_n = 10000000; int Prime_len=400; int[] Prime = new int[Prime_len]; Prime[0] = 2; int k=1; int p=1; while(k<Prime_len){ if(isPrime(p)){ Prime[k++] = p; } p+=2; } long result = 0; double minvalue=10000; long euler = 0 ; for(long n = 2;n<Max_n;n++){ euler = phi3(n,Prime); if(isPerm(euler,n)){ double temp = n/(euler*1.0); if(temp<minvalue){ minvalue = temp; result = n; } } } System.out.println(result); }
结果:
// 8319823 // running time=58s426ms
时间少了30s
这里缺点是要取多少个素数?
我从100,200,300,400,在400的时候结果是正确的
全部程序:
package project61; public class P70{ void run2(){ long Max_n = 10000000; int Prime_len=400; int[] Prime = new int[Prime_len]; Prime[0] = 2; int k=1; int p=1; while(k<Prime_len){ if(isPrime(p)){ Prime[k++] = p; } p+=2; } long result = 0; double minvalue=10000; long euler = 0 ; for(long n = 2;n<Max_n;n++){ euler = phi3(n,Prime); if(isPerm(euler,n)){ double temp = n/(euler*1.0); if(temp<minvalue){ minvalue = temp; result = n; } } } System.out.println(result); } // 8319823 // running time=58s426ms long phi3(long n,int[] Prime){ long res = 0; if(n==1) return 0; int len = Prime.length; res = n; int i=0; //&& n>=Prime[i] while(i <len && n>=Prime[i] ){ if(n%Prime[i]==0){ res/=Prime[i]; res*=(Prime[i]-1); while(n%Prime[i]==0){ n/=Prime[i]; } } i++; } if(n>1){ res/=n; res*=(n-1); } return res; } void run(){ long Max_n = 10000000; long result = 0; double minvalue=10000; long euler = 0 ; for(long n = 2;n<Max_n;n++){ euler = phi2(n); if(isPerm(euler,n)){ double temp = n/(euler*1.0); if(temp<minvalue){ minvalue = temp; result = n; } } } System.out.println(result); } boolean isPerm(long a,long b){ int[] label = new int[10]; while(a!=0&&b!=0){ label[(int) (a%10)]+=1; label[(int) (b%10)]-=1; a/=10; b/=10; } if(a!=0) return false; if(b!=0) return false; for(int i=0;i<10;i++) if(label[i]!=0) return false; return true; } boolean isPrime(int n){ if(n==2||n==3||n==5||n==7||n==11) return true; if(n<2||n%2==0||n%3==0) return false; for(int i=5;i<=Math.sqrt(n)+1;i++){ if(n%i==0) return false; } return true; } long phi2(long n){ long res = 0; if(n==1) return 0; int pi=2; res = n; while(pi*pi <=n){ if(n%pi==0){ res/=pi; res*=(pi-1); while(n%pi==0){ n/=pi; } } pi++; } if(n>1){ res/=n; res*=(n-1); } return res; } // 8319823 // running time=89s43ms // public static void main(String[] args){ long start = System.currentTimeMillis(); new P70().run2(); long end = System.currentTimeMillis(); long time = end - start; System.out.println("running time="+time/1000+"s"+time%1000+"ms"); } }
一直感觉这个程序还可以优化
是否还有好的算法
![]()
在解题论坛上,有个解答程序看不懂,然后我就敲成java,用时8s。。。快了好多的
long[] cal_phi(){ long[] phi=new long[Max_n+1]; for(int i=1;i<Max_n;i++){ phi[i]+=i; for(int j=2*i;j<Max_n;j+=i) phi[j]-=phi[i]; } return phi; }
8s
这个是产生Max_n的所以的欧拉函数,这个虽然是两层循环,但是效率很高的,变量完就得到欧拉函数值
下面一种形式:
long[] cal_phi2(){ long[] phi = new long[Max_n+1]; for(int i=1;i<Max_n;i++) phi[i] = i; for(int i=2;i<Max_n;i++){ if(phi[i]==i) phi[i] = i - 1; for(int j=2*i;j<Max_n;j+=i) phi[j]*=(1-1.0/i); } return phi; }
15s
// 8319823 // running time=14s577ms
至于上面是何总介绍?我还不明白
在解题报告中,还有一种是利用到素数,奇数,偶数还不明白为什么的。
全部程序:
package project61; public class P70_1{ int Max_n = 10000000; void run(){ long[] phi=cal_phi(); int result = 0; double minvalue = 10000.0; for(int n=2;n<Max_n;n++){ long euler = phi[n]; if(isPerm(euler,n)){ double temp = n/(euler*1.0); if(temp<minvalue){ minvalue = temp; result = n; } } } System.out.println(result); } long[] cal_phi(){ long[] phi=new long[Max_n+1]; for(int i=1;i<Max_n;i++){ phi[i]+=i; for(int j=2*i;j<Max_n;j+=i) phi[j]-=phi[i]; } return phi; } // 8319823 // running time=7s855ms long[] cal_phi2(){ long[] phi = new long[Max_n+1]; for(int i=1;i<Max_n;i++) phi[i] = i; for(int i=2;i<Max_n;i++){ if(phi[i]==i) phi[i] = i - 1; for(int j=2*i;j<Max_n;j+=i) phi[j]*=(1-1.0/i); } return phi; } // 8319823 // running time=14s577ms boolean isPerm(long a,long b){ int[] label = new int[10]; while(a!=0&&b!=0){ label[(int) (a%10)]+=1; label[(int) (b%10)]-=1; a/=10; b/=10; } if(a!=0) return false; if(b!=0) return false; for(int i=0;i<10;i++) if(label[i]!=0) return false; return true; } boolean isPrime(long n){ if(n==2||n==3||n==5||n==7) return true; if(n<2||n%2==0||n%3==0) return false; for(int i=5;i<=Math.sqrt(n);i++) if(n%i==0) return false; return true; } public static void main(String[] args){ long start = System.currentTimeMillis(); new P70_1().run(); long end = System.currentTimeMillis(); long time = end - start; System.out.println("running time="+time/1000+"s"+time%1000+"ms"); } }
上面的程序用Python实习时间好长的![]()