The Fibonacci sequence is defined by the recurrence relation:
It turns out that F541, which contains 113 digits, is the first Fibonacci number for which the last nine digits are 1-9 pandigital (contain all the digits 1 to 9, but not necessarily in order). And F2749, which contains 575 digits, is the first Fibonacci number for which the first nine digits are 1-9 pandigital.
Given that Fk is the first Fibonacci number for which the first nine digits AND the last nine digits are 1-9 pandigital, find k.
斐波那契数列由如下递归关系生成:
可以发现,包含有113位数字的F541是第一个后9位数字是1至9全数字(包含1至9所有的数字,但不一定按照从小到大的顺序)的斐波那契数,而包含有575位数字的F2749是第一个前9位数字是1至9全数字的斐波那契数。
若Fk是第一个前9位数字和后9位数字都是1至9全数字的斐波那契数,求k。
解题
直接暴力,可取,时间过长,没有那么多时间跑
mathblog 算了下4.6天,完全不能容忍的

想到直接根据公式计算,但是也不是很好的,Mathblog中提到了,只求fib的第九位,判断是否是0-9的数
利用 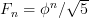 ,估算fib的值,或者说,当n很大的时候这个数和fib对于位的数是相等的,在题解中也看到好多都是根据这个思想计算的
,估算fib的值,或者说,当n很大的时候这个数和fib对于位的数是相等的,在题解中也看到好多都是根据这个思想计算的
其推到过程

Python
运行结果不对
不知道为什么
# coding=gbk import time as time import re import math import numpy as np import math def run(): f1 = 1 f2 = 1 index = 1 while True: f = (f1 + f2)%1000000000 f1 = f2 f2 = f index +=1 if isPandigital(f): if first9(index): print index break def first9(n): t = n *0.20898764024997873 - 0.3494850021680094 last9 = int(10**(t - int(t)+8 )) return isPandigital(last9) def isPandigital(s): if len(str(s)) !=9:return False return set(str(s)) == set('123456789') t0 = time.time() run() t1 = time.time() print "running time=",(t1-t0),"s"